Практическа работа: Преобразуване на графики на функции. Производна Геометричното значение на производната

Производната на функция $y = f(x)$ в дадена точка $х_0$ е границата на съотношението на нарастването на функцията към съответното увеличение на нейния аргумент, при условие че последното клони към нула:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

Диференцирането е операция за намиране на производна.

Таблица на производните на някои елементарни функции

функция	Производна
$c$	$0$
$x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

Основни правила за диференциране

1. Производната на сбора (разликата) е равна на сбора (разликата) на производните

$(f(x) ± g(x))"= f"(x)±g"(x)$

Намерете производната на функцията $f(x)=3x^5-cosx+(1)/(x)$

Производната на сбора (разликата) е равна на сбора (разликата) на производните.

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. Производна на продукт

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

Намерете производната $f(x)=4x cosx$

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. Производна на частното

$((f(x))/(g(x)"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

Намерете производната $f(x)=(5x^5)/(e^x)$

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. Производната на сложна функция е равна на произведението на производната на външната функция и производната на вътрешната функция

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5= -5sin(5x)$

Физическото значение на производната

Ако материална точка се движи по права линия и нейната координата се променя в зависимост от времето по закона $x(t)$, тогава моментната скорост на тази точка е равна на производната на функцията.

Точката се движи по координатната права по закона $x(t)= 1.5t^2-3t + 7$, където $x(t)$ е координатата в момент $t$. В кой момент скоростта на точката ще бъде равна на $12$?

1. Скоростта е производна на $x(t)$, така че нека намерим производната на дадената функция

$v(t) = x"(t) = 1,5 2t -3 = 3t -3$

2. За да намерим в кой момент от време $t$ скоростта е била равна на $12$, съставяме и решаваме уравнението:

Геометричният смисъл на производната

Спомнете си, че уравнението на права линия, която не е успоредна на координатните оси, може да бъде записано като $y = kx + b$, където $k$ е наклонът на правата линия. Коефициентът $k$ е равен на тангенса на наклона между правата линия и положителната посока на оста $Ox$.

Производната на функцията $f(x)$ в точка $x_0$ е равна на наклона $k$ на допирателната към графиката в дадената точка:

Следователно можем да направим общо равенство:

$f"(x_0) = k = tgα$

На фигурата допирателната към функцията $f(x)$ нараства, следователно коефициентът $k > 0$. Тъй като $k > 0$, тогава $f"(x_0) = tgα > 0$. Ъгълът $α$ между допирателната и положителната посока $Ox$ е остър.

На фигурата допирателната към функцията $f(x)$ намалява, следователно коефициентът $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На фигурата допирателната към функцията $f(x)$ е успоредна на оста $Ох$, следователно коефициентът $k = 0$, следователно $f"(x_0) = tg α = 0$. Точката $ x_0$, при което $f "(x_0) = 0$, извикан екстремум.

Фигурата показва графиката на функцията $y=f(x)$ и допирателната към тази графика, начертана в точката с абсцисата $x_0$. Намерете стойността на производната на функцията $f(x)$ в точка $x_0$.

Следователно допирателната към графиката нараства, $f"(x_0) = tg α > 0$

За да намерим $f"(x_0)$, намираме тангентата на наклона между тангентата и положителната посока на оста $Ox$. За да направим това, допълваме тангентата към триъгълника $ABC$.

Намерете тангенса на ъгъла $BAC$. (Тангенса на остър ъгъл в правоъгълен триъгълник е съотношението на срещуположния катет към съседния катет.)

$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$

$f"(x_0) = tg ВИЕ = $0,25

Отговор: 0,25 долара

Производната се използва и за намиране на интервалите на нарастващи и намаляващи функции:

Ако $f"(x) > 0$ на интервал, тогава функцията $f(x)$ нараства на този интервал.

Ако $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Фигурата показва графиката на функцията $y = f(x)$. Намерете сред точките $х_1,х_2,х_3…х_7$ онези точки, в които производната на функцията е отрицателна.

В отговор запишете броя на точките от данни.

В задача № 13 от Единния държавен изпит по математика на основно ниво ще трябва да демонстрирате уменията и знанията за една от концепциите за поведението на функция: производни в точка или скорости на нарастване или намаляване. Теорията за тази задача ще бъде добавена малко по-късно, но това няма да ни попречи да анализираме подробно няколко типични варианта.

Анализ на типични опции за задачи № 14 USE по математика на основно ниво

Опция 14MB1

Графиката показва зависимостта на температурата от времето в процеса на загряване на двигателя на автомобила. Хоризонталната ос показва времето в минути, изтекло от стартирането на двигателя; по вертикалната ос е температурата на двигателя в градуси по Целзий.

Използвайки графиката, свържете всеки интервал от време с характеристиките на процеса на загряване на двигателя в този интервал.

В таблицата под всяка буква посочете съответния номер.

Алгоритъм за изпълнение:

Изберете интервала от време, в който температурата е спаднала.
Прикрепете линийка към 30°C и определете интервала от време, в който температурата е била под 30°C.

Решение:

Нека изберем интервала от време, в който температурата е спаднала. Този участък се вижда с невъоръжено око, започва 8 минути от момента на стартиране на двигателя.

Приложете линийка към 30°C и определете интервала от време, в който температурата е била под 30°C.

Под линийката ще има секция, съответстваща на интервала от време 0 - 1 мин.

С помощта на молив и линийка намираме в какъв интервал от време температурата е била в диапазона от 40 ° C до 80 ° C.

От точките, съответстващи на 40°C и 80°C, пускаме перпендикулярите върху графиката, а от получените точки пускаме перпендикулярите върху времевата ос.

Виждаме, че този температурен интервал съответства на времеви интервал от 3 - 6,5 минути. Тоест от дадените в условието 3 - 6 мин.

Изберете липсващия отговор, като използвате метода на елиминиране.

Опция 14MB2

Решение:

Нека анализираме графиката на функция A. Ако функцията нараства, тогава производната е положителна и обратно. Производната на функцията е равна на нула в точките на екстремума.

Първо, функцията A нараства, т.е. производната е положителна. Това съответства на графиките на производни 2 и 3. В максималната точка на функцията x = -2, тоест в тази точка, производната трябва да е равна на нула. Това условие съответства на графика номер 3.

Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 4. Максималната точка на функцията x \u003d -2, т.е. в тази точка производната трябва да бъде равна на нула. Това условие съответства на графика номер 4.

Първо, функцията B нараства, т.е. производната е положителна. Това съответства на графиките на производни 2 и 3. Максималната точка на функцията x = 1, тоест в тази точка производната трябва да е равна на нула. Това условие съответства на графика номер 2.

Чрез метода на елиминиране можем да определим, че графиката на функцията Г съответства на графиката на производната под номер 1.

Отговор: 3421.

Опция 14MB3

Алгоритъмът за изпълнение на всяка от функциите:

Определете интервалите на нарастващи и намаляващи функции.
Определете максималните и минималните точки на функциите.
Направете заключения, съпоставете предложените графици.

Решение:

Нека анализираме графиката на функция A.

Ако функцията е нарастваща, тогава производната е положителна и обратно. Производната на функцията е равна на нула в точките на екстремума.

Екстремалната точка е точката, в която се достига максималната или минималната стойност на функцията.

Първо, функцията A нараства, т.е. производната е положителна. Това съответства на графиките на производните 3 и 4. В максималната точка на функцията x=0, тоест в тази точка, производната трябва да е равна на нула. Това условие съответства на графика номер 4.

Нека анализираме графиката на функция B.

Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производните 1 и 2. Минималната точка на функцията x=-1, тоест в тази точка производната трябва да е равна на нула. Това условие съответства на графика номер 2.

Нека анализираме графиката на функцията B.

Първо, функцията B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 2. Минималната точка на функцията x \u003d 0, т.е. в тази точка производната трябва да бъде равна на нула. Това условие съответства на графика номер 1.

Чрез метода на елиминиране можем да определим, че графиката на функцията Г съответства на графиката на производната под номер 3.

Отговор: 4213.

Опция 14MB4

Фигурата показва графика на функция и допирателни, начертани към нея в точки с абциси A, B, C и D.Дясната колона показва стойностите на производната в точки A, B, C и D. С помощта на графиката съпоставете всяка точка със стойността на производната на функцията в нея.

ТОЧКИ
НО
AT
ОТ
д

ПРОИЗВОДНИ СТОЙНОСТИ
1) –4
2) 3
3) 2/3
4) -1/2

Припомнете си какво означава производната, а именно нейната стойност в точката - стойността на производната функция в точка е равна на тангенса на наклона (коефициента) на тангенса.

В отговорите имаме два положителни и два отрицателни варианта. Както си спомняме, ако коефициентът е директен (графика y = kx + b) е положителна, тогава линията нараства; ако е отрицателна, тогава линията намалява.

Имаме две възходящи линии - в точката A и D. Сега нека си припомним какво означава стойността на коефициента k?

Коефициентът k показва колко бързо се увеличава или намалява функцията (всъщност самият коефициент k е производната на функцията y = kx + b).

Следователно k \u003d 2/3 съответства на по-нежна права линия - D, а k \u003d 3 - A.

По същия начин, в случай на отрицателни стойности: точка B съответства на по-стръмна права линия с k = -4, а точка C - -1/2.

Опция 14MB5

На фигурата точките показват обема на месечните продажби на нагреватели в магазин за домакински уреди. Месеците са посочени хоризонтално, броят на продадените нагреватели е посочен вертикално. За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, свържете всеки от посочените периоди от време с характеристиките на продажбите на нагреватели.

Алгоритъм за изпълнение

Анализираме частите от графиката, съответстващи на различни сезони. Ние формулираме ситуациите, показани на графиката. Ние намираме най-подходящите отговори за тях.

Решение:

През зимата броят на продажбите надхвърли 120 броя / месец и се увеличава през цялото време. Тази ситуация съответства на отговор 3. Тези. получаваме: А-3.

През пролетта продажбите постепенно паднаха от 120 нагревателя на месец до 50. Вариант № 2 е най-близо до тази формулировка. Ние имаме: B–2.

През лятото броят на продажбите не се промени и беше минимален. Втората част на тази формулировка не е отразена в отговорите, а само № 4 е подходяща за първата. Следователно имаме: НА 4.

През есента продажбите нараснаха, но броят им не надхвърли 100 броя през нито един от месеците. Тази ситуация е описана във вариант №1. Получаваме: G–1.

Опция 14MB6

Графиката показва зависимостта на скоростта на редовен автобус от времето. Вертикалната ос показва скоростта на автобуса в km/h, хоризонталната ос показва времето в минути от началото на автобуса.

С помощта на графиката съпоставете всеки интервал от време с характеристиката на движението на автобуса в този интервал.

Алгоритъм за изпълнение

Ние определяме цената на разделението по хоризонтална и вертикална скала.
Анализираме последователно предложените твърдения 1–4 от дясната колона („Характеристики“). Сравняваме ги с времеви интервали от лявата колона на таблицата, намираме двойки "буква-число" за отговор.

Решение:

Делението на хоризонталната скала е 1 s, на вертикалната скала е 20 km/h.

Когато автобусът спре, скоростта му е 0. За 2 минути подред автобусът е имал нулева скорост само от 9-та до 11-та минута. Това време попада в интервала от 8-12 минути. Така че имаме няколко за отговор: B–1.
Автобусът е имал скорост от 20 км/ч или повече за няколко периода от време. Освен това вариант А не е подходящ тук, защото например на 7-ата минута скоростта е била 60 км/ч, вариант Б - защото вече е приложен, вариант Г - защото в началото и в края на интервала автобусът имаше нулева скорост. В този случай е подходящ вариант Б (12–16 минути); на този интервал автобусът започва да се движи със скорост 40 км/ч, след това ускорява до 100 км/м и след това постепенно намалява скоростта до 20 км/ч. Така че имаме: В 2.
Тук се задава ограничението на скоростта. Не разглеждаме варианти B и C. Останалите интервали A и G са подходящи. Следователно би било правилно да разгледаме първо 4-та опция и след това отново да се върнем към 3-та.
От двата оставащи интервала само 4–8 минути са подходящи за характеристика № 4, тъй като на този интервал (на 6-та минута) е имало спиране. В интервала от 18–22 минути няма спирания. Получаваме: А-4. От това следва, че за характеристика № 3 е необходимо да се вземе интервалът Г, т.е. се оказва двойка G–3.

Опция 14MB7

Пунктираната фигура показва нарастването на населението на Китай от 2004 до 2013 г. Годината е посочена хоризонтално, прирастът на населението като процент (увеличение на населението спрямо предходната година) е посочен вертикално. За по-голяма яснота точките са свързани с линия.

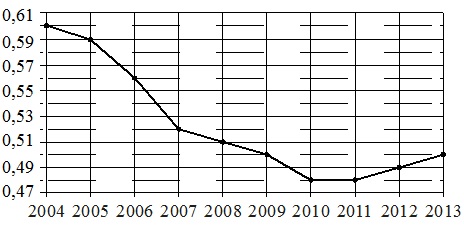
Като използвате диаграмата, свържете всеки от посочените периоди от време с характеристика на нарастването на населението на Китай през този период..

Алгоритъм за изпълнение

Определете стойността на разделението на вертикалния мащаб на картината. Намира се като разликата между двойка съседни стойности на скала, разделена на 2 (тъй като има 2 деления между две съседни стойности).
Анализираме характеристиките 1–4, дадени последователно в условието (лява таблична колона). Сравняваме всеки от тях с определен период от време (дясна колона на таблицата).

Решение:

Стойността на делението на вертикалната скала е 0,01%.

Спадът на растежа продължи непрекъснато от 2004 до 2010 г. През 2010-2011 г. увеличението беше постоянно минимално, а от 2012 г. започна да се увеличава. Тези. Растежът спря през 2010 г. Тази година е в периода 2009-2011 г. Съответно имаме: В 1.
Най-големият спад в растежа трябва да се счита за най-„рязко“ падащата линия на графиката на фигурата. Попада в периода 2006-2007 г. и е 0,04% годишно (0,59–0,56=0,04% през 2006 г. и 0,56–0,52=0,04% през 2007 г.). От тук получаваме: А-2.
Ръстът, посочен в характеристика № 3, започва през 2007 г., продължава през 2008 г. и завършва през 2009 г. Това съответства на период от време B, т.е. ние имаме: B–3.
Прирастът на населението започна да се увеличава след 2011 г., т.е. през 2012–2013 г Следователно получаваме: G–4.

Опция 14MB8

Фигурата показва графика на функция и допирателни, начертани към нея в точки с абциси A, B, C и D.

Дясната колона показва стойностите на производната на функцията в точки A, B, C и D. С помощта на графиката съпоставете всяка точка със стойността на производната на функцията в нея.

Алгоритъм за изпълнение

Разглеждаме двойка допирателни, които имат остър ъгъл с положителната посока на оста x. Сравняваме ги, намираме съвпадение между двойката съответстващи стойности на производните.
Разглеждаме двойка допирателни, образуващи тъп ъгъл с положителната посока на оста x. Сравняваме ги по модул, определяме съответствието на техните стойности на производни между двете останали в дясната колона.

Решение:

Остър ъгъл с положителна посока на оста x се образува от производни в t.B и t.C. Тези производни имат положителни стойности. Следователно тук трябва да избирате между стойностите № 1 и 3. Прилагайки правилото, че ако ъгълът е по-малък от 45 0, тогава производната е по-малка от 1, а ако е повече, тогава повече от 1, заключаваме: в t.B производната по модул е по-голяма от 1, в t.C - по-малка от 1. Това означава, че можете да направите двойки за отговора: НА 3и S-1.

Производните в t.A и t.D образуват тъп ъгъл с положителната посока на оста x. И тук прилагаме същото правило, леко перифразирайки го: колкото повече допирателната в точката е „притисната“ към линията на абсцисната ос (към нейната отрицателна посока), толкова по-голяма е тя в абсолютна стойност. Тогава получаваме: производната в точка А е по-малка по абсолютна стойност от производната в точка D. От тук имаме двойки за отговор: А-2и D-4.

Опция 14MB9

Точките на фигурата показват средната дневна температура на въздуха в Москва през януари 2011 г. Датите от месеца са посочени хоризонтално, температурите в градуси по Целзий са посочени вертикално. За по-голяма яснота точките са свързани с линия.

С помощта на фигурата съпоставете всеки от посочените периоди от време с характеристика на промяна на температурата.

Алгоритъм за изпълнение

Ние анализираме последователно характеристики 1–4 (дясна колона), като използваме графиката на фигурата. Поставяме всеки от тях в съответствие с определен период от време (лявата колона).

Решение:

Повишаване на температурата се наблюдава само в края на периода 22–28 януари. Тук на 27-и и 28-и тя се е повишила съответно с 1 и 2 градуса. В края на периода 1–7 януари температурата е стабилна (–10 градуса), в края на 8–14 и 15–21 януари се понижава (от –1 до –2 и от –11 до –12 степени, съответно). Следователно получаваме: G–1.
Тъй като всеки период обхваща 7 дни, температурата трябва да се анализира от 4-ия ден на всеки период. Само от 4 до 7 януари температурата остава непроменена 3–4 дни. Така получаваме отговора: А-2.
Минималната месечна температура се наблюдава на 17 януари. Това число попада в периода 15-21 януари. От тук имаме няколко: НА 3.
Температурният максимум падна на 10 януари и достигна +1 градус. Тази дата попада в периода 8-14 януари. Така че имаме: Б-4.

Опция 14MB10

Алгоритъм за изпълнение

Стойността на функцията в точка е положителна, ако тази точка се намира над оста Ox.
Производната в точка е по-голяма от нула, ако допирателната към тази точка образува остър ъгъл с положителната посока на оста x.

Решение:

Точка A. Тя е под оста Ox, което означава, че стойността на функцията в нея е отрицателна. Ако начертаем допирателна в нея, то ъгълът между нея и положителната посока Ox ще бъде около 90 0, т.е. образува остър ъгъл. Така че в този случай е подходяща характеристика номер 3. Тези. ние имаме: А-3.

Точка B. Намира се над оста Ox, т.е. точката има положителна функционална стойност. Допирателната в тази точка ще бъде доста близо до абсцисната ос, образувайки тъп ъгъл (малко по-малко от 180 0) с положителната си посока. Съответно, производната в този момент е отрицателна. Така тук е подходяща характеристика 1. Получаваме отговора: В 1.

Точка C. Точката е разположена под оста Ox, допирателната в нея образува голям тъп ъгъл с положителната посока на абсцисната ос. Тези. в t.C стойността както на функцията, така и на производната е отрицателна, което съответства на характеристика № 2. Отговор: S-2.

Точка D. Точката е разположена над оста Ox, а тангентата в нея образува остър ъгъл с положителната посока на оста. Това предполага, че както стойността на функцията, така и стойността на производната тук са по-големи от нула. Отговор: D-4.

Опция 14MB11

На фигурата точките показват обема на месечните продажби на хладилници в магазин за домакински уреди. Месеците са посочени хоризонтално, броят на продадените хладилници е посочен вертикално. За по-голяма яснота точките са свързани с линия.

С помощта на фигурата съпоставете всеки от посочените времеви периоди с характеристиките на продажбите на хладилници.

Правата y=3x+2 е допирателна към графиката на функцията y=-12x^2+bx-10. Намерете b, като се има предвид, че абсцисата на допирната точка е по-малка от нула.

Покажи решение

Решение

Нека x_0 е абсцисата на точката от графиката на функцията y=-12x^2+bx-10, през която минава допирателната към тази графика.

Стойността на производната в точката x_0 е равна на наклона на тангентата, т.е. y"(x_0)=-24x_0+b=3. От друга страна, допирателната точка принадлежи както на графиката на функцията, така и на тангенс, т.е. -12x_0^2+bx_0-10= 3x_0 + 2. Получаваме система от уравнения \begin(cases) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \край (случаи)

Решавайки тази система, получаваме x_0^2=1, което означава или x_0=-1, или x_0=1. Съгласно състоянието на абсцисата точките на допир са по-малки от нула, следователно x_0=-1, тогава b=3+24x_0=-21.

Отговор

Състояние

Фигурата показва графика на функцията y=f(x) (която е начупена линия, съставена от три прави сегмента). Като използвате фигурата, изчислете F(9)-F(5), където F(x) е една от първоизводните на f(x).

Покажи решение

Решение

Според формулата на Нютон-Лайбниц разликата F(9)-F(5), където F(x) е една от първоизводните на функцията f(x), е равна на площта на криволинейния трапец, ограничен по графиката на функцията y=f(x), прави y=0 , x=9 и x=5. Според графиката определяме, че посоченият криволинеен трапец е трапец с основи равни на 4 и 3 и височина 3.

Площта му е равна на \frac(4+3)(2)\cdot 3=10,5.

Отговор

Източник: „Математика. Подготовка за матура-2017г. ниво на профил. Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графика на y \u003d f "(x) - производната на функцията f (x), определена в интервала (-4; 10). Намерете интервалите на намаляваща функция f (x). Във вашия отговор , посочете дължината на най-големия от тях.

Покажи решение

Решение

Както знаете, функцията f (x) намалява на тези интервали, във всяка точка от които производната f "(x) е по-малка от нула. Като се има предвид, че е необходимо да се намери дължината на най-големия от тях, три такива интервала се разграничават естествено от фигурата: (-4; -2) ;(0;3);(5;9).

Дължината на най-голямата от тях - (5; 9) е равна на 4.

Отговор

Източник: „Математика. Подготовка за матура-2017г. ниво на профил. Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графика на y \u003d f "(x) - производната на функцията f (x), определена на интервала (-8; 7). Намерете броя на максималните точки на функцията f (x), принадлежащи към интервала [-6; -2].

Покажи решение

Решение

Графиката показва, че производната f "(x) на функцията f (x) променя знака от плюс на минус (ще има максимум в такива точки) точно в една точка (между -5 и -4) от интервала [ -6; -2 Следователно има точно една максимална точка на интервала [-6;-2].

Отговор

Източник: „Математика. Подготовка за матура-2017г. ниво на профил. Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графика на функцията y=f(x), дефинирана на интервала (-2; 8). Определете броя на точките, в които производната на функцията f(x) е равна на 0 .

Покажи решение

Решение

Ако производната в дадена точка е равна на нула, тогава допирателната към графиката на функцията, начертана в тази точка, е успоредна на оста Ox. Следователно намираме такива точки, в които допирателната към графиката на функцията е успоредна на оста Ox. На тази диаграма такива точки са екстремни точки (максимални или минимални точки). Както можете да видите, има 5 точки на екстремум.

Отговор

Източник: „Математика. Подготовка за матура-2017г. ниво на профил. Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Правата y=-3x+4 е успоредна на допирателната към графиката на функцията y=-x^2+5x-7. Намерете абсцисата на точката на контакт.

Покажи решение

Решение

Наклонът на правата към графиката на функцията y=-x^2+5x-7 в произволна точка x_0 е y"(x_0). Но y"=-2x+5, така че y"(x_0)=- 2x_0 + 5. Ъгловият коефициент на правата y=-3x+4, определен в условието, е -3.

Получаваме: x_0 = 4.

Отговор

Източник: „Математика. Подготовка за матура-2017г. ниво на профил. Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графика на функцията y=f(x) и отбелязани точки -6, -1, 1, 4 по оста x. В коя от тези точки стойността на производната е най-малка? Моля, посочете тази точка в отговора си.

Назад напред

внимание! Визуализацията на слайда е само за информационни цели и може да не представя пълния обем на презентацията. Ако се интересувате от тази работа, моля, изтеглете пълната версия.

Тип урок:повторение и обобщение.

Форма на урока:консултативен урок.

Цели на урока:

образователен: повтарят и обобщават теоретичните знания по темите: „Геометричен смисъл на производната” и „Приложение на производната за изучаване на функциите”; разглеждат всички типове задачи от В8, които се срещат на изпита по математика; предоставят на учениците възможност да проверят знанията си чрез самостоятелно решаване на задачи; научи как да попълва изпитната форма с отговори;
развиващи се: да насърчава развитието на комуникацията като метод за научно познание, семантична памет и доброволно внимание; формирането на такива ключови компетенции като сравнение, сравнение, класификация на обекти, определяне на адекватни начини за решаване на учебен проблем въз основа на дадени алгоритми, способност за самостоятелно действие в ситуация на несигурност, контрол и оценка на собствените дейности, намиране и премахване на причините за възникналите затруднения;
образователен: развиват комуникативните компетенции на учениците (култура на общуване, умение за работа в група); допринасят за развитието на потребността от самообразование.

Технологии: развиващо обучение, ИКТ.

Методи на обучение:словесно, визуално, практично, проблемно.

Форми на работа:индивидуални, фронтални, групови.

Учебно-методическа помощ:

1. Алгебра и началото на математическия анализ 11 клас: учебник. За общо образование Институции: основни и профилни. нива / (Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин); под редакцията на А. Б. Жижченко. - 4-то изд. - М .: Образование, 2011.

2. ИЗПОЛЗВАНЕ: 3000 задачи с отговори по математика. Всички задачи от група B / A.L. Семьонов, И.В. Яшченко и др.; редактиран от A.L. Семьонова, И.В. Ященко. - М .: Издателство "Изпит", 2011 г.

3. Отворете банка за работа.

Оборудване и материали за урока:проектор, екран, компютър за всеки ученик с инсталирана презентация, разпечатка на бележка за всички ученици (Приложение 1)и резултатен лист Приложение 2) .

Предварителна подготовка за урока:като домашна работа учениците се приканват да повторят теоретичния материал на учебника по темите: „Геометричният смисъл на производната“, „Приложение на производната към изследването на функциите“; класът е разделен на групи (по 4 души), всяка от които има ученици от различни нива.

Обяснение към урока:Този урок се провежда в 11 клас на етапа на повторение и подготовка за изпита. Урокът е насочен към повторение и обобщение на теоретичния материал, приложението му при решаване на изпитни задачи. Продължителност на урока - 1,5 часа .

Този урок не е приложен към учебника, така че може да се проведе по време на работа по всякакви учебни материали. Освен това този урок може да бъде разделен на два отделни и да се проведе като последен урок по разглежданите теми.

По време на часовете

I. Организационен момент.

II. Урок за поставяне на цели.

III. Повторение по темата „Геометричен смисъл на производната“.

Устна фронтална работа с помощта на проектор (слайдове № 3-7)

Групова работа: решаване на проблеми със съвети, отговори, със съвети на учителя (слайдове № 8-17)

IV. Самостоятелна работа 1.

Учениците работят самостоятелно на компютър (слайдове № 18-26), отговорите им се вписват в листа за оценка. Ако е необходимо, можете да вземете съвет от учителя, но в този случай ученикът ще загуби 0,5 точки. Ако ученикът се справи с работата по-рано, тогава може да избере да реши допълнителни задачи от сборника, стр. 242, 306-324 (допълнителните задачи се оценяват отделно).

V. Взаимна проверка.

Учениците обменят листове за оценка, проверяват работата на приятел, дават точки (слайд № 27)

VI. Корекция на знанията.

VII. Повторение по темата „Приложение на производната към изследването на функциите“

Устна фронтална работа с помощта на проектор (слайдове № 28-30)

Групова работа: решаване на проблеми с подкани, отговори, със съвети на учителя (слайдове № 31-33)

VIII. Самостоятелна работа 2.

Учениците работят индивидуално на компютър (слайдове № 34-46), вписват отговорите си в листа за отговори. Ако е необходимо, можете да вземете съвет от учителя, но в този случай ученикът ще загуби 0,5 точки. Ако ученикът се справи с работата по-рано, тогава може да избере да реши допълнителни задачи от сборника, стр. 243-305 (допълнителните задачи се оценяват отделно).

IX. Взаимна проверка.

Учениците обменят листове за оценка, проверяват работата на приятел, дават точки (слайд № 47).

X. Корекция на знанията.

Учениците отново работят в своите групи, обсъждат решението, коригират грешките.

XI. Обобщаване.

Всеки ученик изчислява точките си и поставя оценка в листа за оценка.

Учениците предават на учителя листа за оценка и решението на допълнителни задачи.

Всеки ученик получава паметна бележка (слайд № 53-54).

XII. Отражение.

Студентите са помолени да оценят знанията си, като изберат една от фразите:

Разбрах всичко!!!
Трябва да решим още няколко примера.
Кой я измисли тази математика!

XIII. Домашна работа.

За домашна работа се предлага на учениците да изберат решаване на задачи от сборника, стр. 242-334, както и от отворена банка със задачи.

Първо опитайте да намерите обхвата на функцията:

успяхте ли Нека сравним отговорите:

Добре? Много добре!

Сега нека се опитаме да намерим диапазона на функцията:

намерени? Сравнете:

Съгласно ли е? Много добре!

Нека отново да работим с графиките, само че сега е малко по-трудно - да намерим както домейна на функцията, така и диапазона на функцията.

Как да намерите както домейна, така и обхвата на функция (разширено)

Ето какво се случи:

С графиките мисля, че се разбра. Сега нека се опитаме да намерим домейна на функцията в съответствие с формулите (ако не знаете как да направите това, прочетете раздела за):

успяхте ли Проверка отговори:

, тъй като коренният израз трябва да е по-голям или равен на нула.
, тъй като е невъзможно да се раздели на нула и радикалният израз не може да бъде отрицателен.
, тъй като, съответно, за всички.
защото не можете да разделите на нула.

Имаме обаче още един момент, който не е изяснен...

Позволете ми да повторя определението и да се съсредоточа върху него:

Забелязано? Думата "само" е много, много важен елемент от нашето определение. Ще се опитам да ви обясня на пръсти.

Да кажем, че имаме функция, дадена от права линия. . Когато заместваме тази стойност в нашето "правило" и получаваме това. Една стойност съответства на една стойност. Можем дори да направим таблица с различни стойности и да начертаем дадена функция, за да проверим това.

"Виж! - казвате вие, - "" се среща два пъти!" Така че може би параболата не е функция? Не, то е!

Фактът, че "" се среща два пъти, далеч не е причина да обвиняваме параболата в неяснота!

Факт е, че при изчисляване за, получихме една игра. И когато пресмятахме с, получихме една игра. Така че, така е, параболата е функция. Вижте диаграмата:

Схванах го? Ако не, ето ви пример от реалния живот, далеч от математиката!

Да кажем, че имаме група кандидати, които се срещнаха при подаване на документи, всеки от които каза в разговор къде живее:

Съгласете се, съвсем реалистично е няколко момчета да живеят в един град, но е невъзможно един човек да живее в няколко града едновременно. Това е, така да се каже, логично представяне на нашата "парабола" - Няколко различни x съответстват на едно и също y.

Сега нека измислим пример, при който зависимостта не е функция. Да кажем, че същите тези хора са казали за какви специалности са кандидатствали:

Тук имаме съвсем различна ситуация: един човек може лесно да кандидатства за едно или няколко направления. Това е един елементкомплекти са поставени в кореспонденция множество елементикомплекти. съответно това не е функция.

Нека проверим знанията ви на практика.

Определете от снимките кое е функция и кое не:

Схванах го? И ето го отговори:

Функцията е - B,E.
Не е функция - A, B, D, D.

Питате защо? Да, ето защо:

Във всички цифри с изключение на AT)и Д)има няколко за един!

Сигурен съм, че сега можете лесно да различите функция от нефункция, да кажете какво е аргумент и какво е зависима променлива, както и да определите обхвата на аргумента и обхвата на функцията. Нека да преминем към следващия раздел - как да дефинираме функция?

Начини за задаване на функция

Какво мислите, че означават думите "задайте функция"? Точно така, това означава да обясним на всички за каква функция говорим в случая. Освен това обяснявайте по такъв начин, че всички да ви разберат правилно и графиките на функциите, начертани от хората според вашето обяснение, да са еднакви.

Как мога да направя това? Как да зададете функция?Най-лесният начин, който вече е използван повече от веднъж в тази статия - с помощта на формула.Пишем формула и като заместваме стойност в нея, изчисляваме стойността. И както си спомняте, формулата е закон, правило, според което за нас и за друг човек става ясно как X се превръща в Y.

Обикновено те правят точно това - в задачите виждаме готови функции, дефинирани с формули, но има и други начини за задаване на функция, за които всички забравят и следователно въпросът „как иначе можете да зададете функция?“ обърква. Нека да разгледаме всичко по ред и да започнем с аналитичния метод.

Аналитичен начин за дефиниране на функция

Аналитичният метод е задача на функция, използваща формула. Това е най-универсалният и изчерпателен и недвусмислен начин. Ако имате формула, тогава знаете абсолютно всичко за функцията - можете да направите таблица със стойности върху нея, можете да изградите графика, да определите къде функцията нараства и къде намалява, като цяло, изследвайте я изцяло.

Нека разгледаме функция. Какво значение има?

"Какво означава?" - ти питаш. Сега ще обясня.

Нека ви напомня, че в нотацията изразът в скоби се нарича аргумент. И този аргумент може да бъде всеки израз, не непременно прост. Съответно, какъвто и да е аргументът (израз в скоби), ние ще го запишем вместо това в израза.

В нашия пример ще изглежда така:

Помислете за друга задача, свързана с аналитичния метод за уточняване на функция, която ще имате на изпита.

Намерете стойността на израза при.

Сигурен съм, че в началото сте се уплашили, когато сте видели такова изражение, но в него няма абсолютно нищо страшно!

Всичко е същото като в предишния пример: какъвто и да е аргументът (изразът в скоби), ние ще го запишем вместо това в израза. Например за функция.

Какво трябва да се направи в нашия пример? Вместо това трябва да напишете и вместо -:

съкратете получения израз:

Това е всичко!

Самостоятелна работа

Сега опитайте сами да намерите значението на следните изрази:

, ако
, ако

успяхте ли Нека сравним нашите отговори: Свикнали сме с факта, че функцията има формата

Дори в нашите примери ние дефинираме функцията по този начин, но аналитично е възможно да дефинираме функцията имплицитно, например.

Опитайте сами да изградите тази функция.

успяхте ли

Ето как го построих.

Какво уравнение получихме?

Правилно! Линеен, което означава, че графиката ще бъде права линия. Нека направим таблица, за да определим кои точки принадлежат на нашата права:

Точно за това говорихме... Едно отговаря на няколко.

Нека се опитаме да нарисуваме какво се случи:

Функция ли е това, което имаме?

Точно така, не! Защо? Опитайте се да отговорите на този въпрос със снимка. Какво получи?

„Защото една стойност съответства на няколко стойности!“

Какво заключение можем да направим от това?

Точно така, една функция не винаги може да бъде изразена експлицитно и това, което е „маскирано“ като функция, не винаги е функция!

Табличен начин за дефиниране на функция

Както подсказва името, този метод е проста чиния. Да да. Като тази, която вече направихме. Например:

Тук веднага забелязахте закономерност - Y е три пъти по-голямо от X. А сега задачата „помислете много добре“: смятате ли, че функция, дадена под формата на таблица, е еквивалентна на функция?

Да не говорим дълго, а да рисуваме!

Така. Начертаваме функция, дадена по двата начина:

Виждате ли разликата? Не става въпрос за отбелязаните точки! Погледни отблизо:

Видяхте ли го сега? Когато задаваме функцията таблично, ние отразяваме върху графиката само тези точки, които имаме в таблицата и правата (както в нашия случай) минава само през тях. Когато дефинираме функция по аналитичен начин, можем да вземем всякакви точки и нашата функция не се ограничава до тях. Ето една такава функция. Помня!

Графичен начин за изграждане на функция

Графичният начин за конструиране на функция е не по-малко удобен. Ние чертаем нашата функция и друго заинтересовано лице може да намери на какво е равно y при определено x и т.н. Графичните и аналитичните методи са сред най-разпространените.

Тук обаче трябва да запомните това, за което говорихме в самото начало - не всяка „качулка“, начертана в координатната система, е функция! Спомняте ли си? За всеки случай ще копирам тук дефиницията на това какво е функция:

По правило хората обикновено назовават точно онези три начина за определяне на функция, които сме анализирали - аналитичен (с помощта на формула), табличен и графичен, напълно забравяйки, че една функция може да бъде описана вербално. Като този? Да, много лесно!

Словесно описание на функцията

Как да опишем функцията вербално? Да вземем нашия скорошен пример - . Тази функция може да бъде описана като "всяка реална стойност на x съответства на нейната тройна стойност." Това е всичко. Нищо сложно. Разбира се, вие ще възразите - „има толкова сложни функции, че е просто невъзможно да се зададат устно!“ Да, има такива, но има функции, които е по-лесно да се опишат устно, отколкото да се зададат с формула. Например: "всяка естествена стойност на x съответства на разликата между цифрите, от които се състои, докато най-голямата цифра, съдържаща се в записа на числото, се приема като умалено." Сега помислете как нашето словесно описание на функцията се прилага на практика:

Най-голямата цифра в дадено число - съответно - се намалява, след което:

Основни видове функции

Сега нека преминем към най-интересното - ще разгледаме основните типове функции, с които сте работили / работите и ще работите в хода на училищната и институтската математика, тоест ще ги опознаем, така да се каже, и дайте им кратко описание. Прочетете повече за всяка функция в съответния раздел.

Линейна функция

Функция на формата, където са реални числа.

Графиката на тази функция е права линия, така че конструкцията на линейна функция се свежда до намиране на координатите на две точки.

Положението на правата върху координатната равнина зависи от наклона.

Обхват на функцията (известен още като диапазон на аргументи) - .

Диапазонът от стойности е.

квадратична функция

Функция на формата, където

Графиката на функцията е парабола, когато клоните на параболата са насочени надолу, когато - нагоре.

Много свойства на квадратична функция зависят от стойността на дискриминанта. Дискриминантът се изчислява по формулата

Позицията на параболата върху координатната равнина спрямо стойността и коефициента е показана на фигурата:

Домейн

Диапазонът на стойностите зависи от екстремума на дадената функция (върха на параболата) и коефициента (посоката на клоновете на параболата)

Обратна пропорционалност

Функцията, дадена от формулата, където

Числото се нарича коефициент на обратна пропорционалност. В зависимост от стойността, клоновете на хиперболата са в различни квадрати:

Домейн - .

Диапазонът от стойности е.

ОБОБЩЕНИЕ И ОСНОВНА ФОРМУЛА

1. Функцията е правило, според което на всеки елемент от множеството се присвоява уникален елемент от множеството.

- това е формула, обозначаваща функция, тоест зависимостта на една променлива от друга;
- променлива или аргумент;
- зависима стойност - променя се при промяна на аргумента, тоест според някаква специфична формула, която отразява зависимостта на една стойност от друга.

2. Валидни стойности на аргументи, или обхватът на функция, е това, което е свързано с възможното, при което функцията има смисъл.

3. Диапазон от стойности на функцията- това е какви стойности приема, с валидни стойности.

4. Има 4 начина за настройка на функцията:

аналитичен (с помощта на формули);
табличен;
графика
словесно описание.

5. Основни видове функции:

: , където, са реални числа;
: , където;
: , където.