Интеграл от синус икс в квадрате. Интегрирование тригонометрических функций: методы и примеры

Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

Воспользовавшись известными тригонометрическими формулами

(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам

(5)

(6)

Пример 1. Найти

Решение. По формуле (2) при

Пример 2. Найти интеграл от тригонометрической функции

Решение. По формуле (3) при

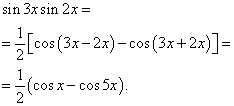
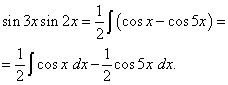
Пример 3. Найти интеграл от тригонометрической функции

Решение. По формуле (4) при получаем следующее преобразование подынтегрального выражения:

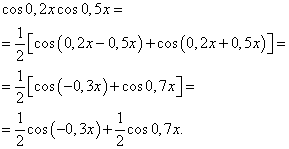
Применяя формулу (6), получим

Интеграл произведения степеней синуса и косинуса одного и того же аргумента

Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

(7)

В частных случаях один из показателей (m или n ) может равняться нулю.

При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cos x dx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sin x dx ) .

Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.

Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что

Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sin x решение сводится к интегрированию многочлена относительно t . Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx , выражая остальную часть подынтегральной функции через cos x и полагая t = cos x . Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса , когда хотя бы один из показателей - нечётный . Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения : когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.

Если же оба показателя m и n – чётные, то, используя тригонометрические формулы

понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится . Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.

Пример 4. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса – нечётный. Поэтому представим

t = sin x (тогда dt = cos x dx ). Тогда получим

Возвращаясь к старой переменной, окончательно найдём

Пример 5. Найти интеграл от тригонометрической функции

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим

и произведём замену переменной t = sin x (тогда dt = cos x dx ). Тогда получим

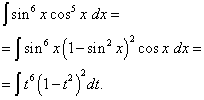
Раскроем скобки

и получим

Возвращаясь к старой переменной, получаем решение

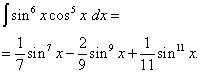
Пример 6. Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:

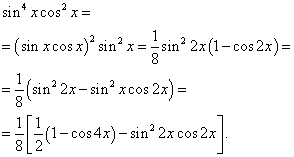
Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x . Тогда (1/2)dt = cos2x dx . Следовательно,

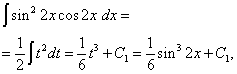
Окончательно получаем

Использование метода замены переменой

Метод замены переменной при интегировании тригонометрических функций можно применять в случаях, когда в подынтегральном выражении присутствует только синус или только косинус, произведение синуса и косинуса, в котором или синус или косинус - в первой степени, тангенс или котангенс, а также частное чётных степеней синуса и косинуса одного и того же аргумента. При этом можно производить перестановки не только sinx = t и sinx = t , но и tgx = t и ctgx = t .

Пример 8. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: , тогда . Получившееся подынтегральное выражение легко интегрируется по таблице интегралов:

Пример 9. Найти интеграл от тригонометрической функции

Решение. Преобразуем тангенс в отношение синуса и косинуса:

Произведём замену переменной: , тогда . Получившееся подынтегральное выражение представляет собой табличный интеграл со знаком минус:

Возвращаясь к первоначальной переменной, окончательно получаем:

Пример 10. Найти интеграл от тригонометрической функции

Решение. Произведём замену переменной: , тогда .

Преобразуем подынтегральное выражение, чтобы применить тригонометрическое тождество :

Производим замену переменной, не забывая перед интегралом поставить знак минус (смотрите выше, чему равно dt ). Далее раскладываем подынтегральное выражение на множители и интегрируем по таблице:

Возвращаясь к первоначальной переменной, окончательно получаем:

Найти интеграл от тригонометрической функции самостоятельно, а затем посмотреть решение

Универсальная тригонометрическая подстановка

Универсальную тригонометрическую подстановку можно применять в случаях, когда подынтегральное выражение не подпадает под случаи, разобранные в предыдущих параграфах. В основном, когда синус или косинус (или и то, и другое) находятся в знаменателе дроби. Доказано, что синус и косинус можно заменить другим выражением, содержащим тангенс половины исходного угла следующим образом:

Но заметим, что универсальная тригонометрическая подстановка часто влечёт за собой довольно сложные алгебраические преобразования, поэтому её лучше применять, когда никакой другой метод не работает. Разберём примеры, когда вместе с универсальной тригонометрической подстановкой используются подведение под знак дифференциала и метод неопределённых коэффициентов.

Пример 12. Найти интеграл от тригонометрической функции

Решение. Решение. Воспользуемся универсальной тригонометрической подстановкой . Тогда
.

Дроби в числителе и знаменателе умножаем на , а двойку выносим и ставим перед знаком интеграла. Тогда

Подробно рассмотрены примеры решений интегралов по частям, подынтегральное выражение которых является произведением многочлена на экспоненту (е в степени х) или на синус (sin x) или на косинус (cos x).

Формула интегрирования по частям

При решении примеров этого раздела, используется формула интегрирования по частям:
;
.

Примеры интегралов, содержащих произведение многочлена и sin x, cos x или e x

Вот примеры таких интегралов:
, , .

Для интегрирования подобных интегралов, многочлен обозначают через u , а оставшуюся часть - через v dx . Далее применяют формулу интегрирования по частям.

Ниже дается подробное решение этих примеров.

Примеры решения интегралов

Пример с экспонентой, е в степени х

Определить интеграл:
.

Решение

Введем экспоненту под знак дифференциала:
e - x dx = - e - x d(-x) = - d(e - x) .

Интегрируем по частям.

здесь
.
Оставшийся интеграл также интегрируем по частям.
.
.
.
Окончательно имеем:
.

Ответ

Пример определения интеграла с синусом

Вычислить интеграл:
.

Решение

Введем синус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 , v = cos(2 x+3) , du = ( x 2 )′ dx

Оставшийся интеграл также интегрируем по частям. Для этого вводим косинус под знак дифференциала.

здесь u = x , v = sin(2 x+3) , du = dx

Окончательно имеем:

Ответ

Пример произведения многочлена и косинуса

Вычислить интеграл:
.

Решение

Введем косинус под знак дифференциала:

Интегрируем по частям.

здесь u = x 2 + 3 x + 5 , v = sin 2 x , du = ( x 2 + 3 x + 5)′ dx

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача - задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти закон движения.
Решение. Пусть s = s(t) - искомый закон движения. Известно, что s"(t) = v(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна gt. Нетрудно догадаться, что $s(t) = \frac{gt^2}{2} $. В самом деле
$s"(t) = \left(\frac{gt^2}{2} \right)" = \frac{g}{2}(t^2)" = \frac{g}{2} \cdot 2t = gt $
Ответ: $s(t) = \frac{gt^2}{2} $

Сразу заметим, что пример решен верно, но неполно. Мы получили $s(t) = \frac{gt^2}{2} $. На самом деле задача имеет бесконечно много решений: любая функция вида $s(t) = \frac{gt^2}{2} + C $, где C - произвольная константа, может служить законом движения, поскольку $\left(\frac{gt^2}{2} +C \right)" = gt $

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s 0 , то из равенства s(t) = (gt 2)/2 + C получаем: s(0) = 0 + С, т. е. C = s 0 . Теперь закон движения определен однозначно: s(t) = (gt 2)/2 + s 0 .

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например: возведение в квадрат (х 2) и извлечение квадратного корня ($\sqrt{x} $), синус (sin x) и арксинус (arcsin x) и т. д. Процесс нахождения производной по заданной функции называют дифференцированием , а обратную операцию, т. е. процесс нахождения функции по заданной производной, - интегрированием .

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у" = f"(x). Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у" = f"(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для $x \in X $ выполняется равенство F"(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х 2 является первообразной для функции у = 2х, поскольку для любого х справедливо равенство (x 2)" = 2х
2) Функция у = х 3 является первообразной для функции у = 3х 2 , поскольку для любого х справедливо равенство (x 3)" = 3х 2
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство (sin(x))" = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) - первообразная для f(x), то kF(x) - первообразная для kf(x).

Теорема 1. Если y = F(x) - первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция $y=\frac{1}{k}F(kx+m) $

Теорема 2. Если y = F(x) - первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл $\textstyle \int F(x)dx $. Сделаем подстановку $x= \varphi(t) $ где $\varphi(t) $ - функция, имеющая непрерывную производную.
Тогда $dx = \varphi " (t) \cdot dt $ и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
$\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt $

Интегрирование выражений вида $\textstyle \int \sin^n x \cos^m x dx $

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям - применение следующей формулы для интегрирования:
$\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du $
или:
$\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx $

Таблица неопределённых интегралов (первообразных) некоторых функций

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac{x^{n+1}}{n+1} +C \;\; (n \neq -1) $$ $$ \int \frac{1}{x} dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac{a^x}{\ln a} +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $$ \int \frac{dx}{\cos^2 x} = \text{tg} x +C $$ $$ \int \frac{dx}{\sin^2 x} = -\text{ctg} x +C $$ $$ \int \frac{dx}{\sqrt{1-x^2}} = \text{arcsin} x +C $$ $$ \int \frac{dx}{1+x^2} = \text{arctg} x +C $$ $$ \int \text{ch} x dx = \text{sh} x +C $$ $$ \int \text{sh} x dx = \text{ch} x +C $$

Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫ sin n xdx , ∫ cos n xdx , n>0
a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.
б) Если n чётное, то пользуемся формулами понижения степени
2. Интегралы вида ∫ tg n xdx , ∫ ctg n xdx , где n – целое.
Необходимо использовать формулы

3. Интегралы вида ∫ sin n x·cos m x dx
а) Пусть m и n разной чётности. Применяем подстановку t=sin x , если n - нечётное либо t=cos x , если m – нечётное.
б) Если m и n чётные, то пользуемся формулами понижения степени
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Интегралы вида

Если числа m и n одинаковой чётности, то используем подстановку t=tg x . Часто бывает удобным применить приём тригонометрической единицы.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx
Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму

Примеры
1. Вычислить интеграл ∫ cos 4 x·sin 3 xdx .
Делаем замену cos(x)=t . Тогда ∫ cos 4 x·sin 3 xdx =
2. Вычислить интеграл .
Делая замену sin x=t , получаем

3. Найти интеграл .
Делаем замену tg(x)=t . Подставляя, получаем

Заметим, что замена ctg(x)=t здесь удобнее, так как тогда , и поэтому

Интегрирование выражений вида R(sinx, cosx)

Пример №1 . Вычислить интегралы:

Решение.
а) Интегрирование выражений вида R(sinx, cosx) , где R - рациональная функция от sin x и cos x , преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t .
Тогда имеем

Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫ R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx , то применяется подстановка cos x = t .
Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx , то подстановка sin x = t .
Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx , то подстановка tgx = t или ctg x = t .

В данном случае для нахождения интеграла

применим универсальную тригонометрическую подстановку tg(x/2) = t .
Тогда
Так как дробь неправильная, то, выделяя целую часть, получим
Возвращась к исходной переменной будем иметь

b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫ R(sinx, cosx) dx имеет вид ∫ sin m x·cos n xdx . В этом частном случае, если m нечетно, следует применить подстановку cos x = t . Если нечетно n , следует применить подстановку sin x = t . Если оба показателя тип - четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:
В данном случае

Ответ:

Интеграл от синуса sin (x) равен косинусу, причем со знаком минус. Многие часто допускает ошибки потому что не может запомнить, что производная от синуса равна минус косинусу, а от косинуса - синусу со знаком плюс.
Те кто изучает первоначальную должны помнить что к правой стороне следует добавить постоянную
Ету постоянную определяют с дополнительной условия.
График синуса имеет вид

Синус нечетная, а косинус - четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл. Поэтому одновременно делим на коэффициент

Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
Далее можем проинтегрировать синус тройного угла
и т.д.
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
Интеграл от синуса одной третьей х равен

Распространенные примеры интегрирования синуса

Пример 1. Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим

Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования

Пример 3. Проинтегрировать выражение sin(7*x).

Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл

Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу

Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.
Решение: Вычисляем первоначальную

Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную

Это и есть ответ к задаче.

Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования

По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.

Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.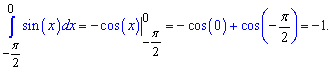

Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.

В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя - это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.

Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю

В то же время площадь заштрихованной фигуры равна единице.