Бінарний розподіл. Біноміальний розподіл дискретної випадкової величини
Розглянемо здійснення схеми Бернуллі, тобто. проводиться серія повторних незалежних випробувань, у кожному з яких дана подія А має одну і ту ж ймовірність, яка не залежить від номера випробування. І для кожного випробування є лише два результати:
1) подія А – успіх;
2) подія – неуспіх,
з постійними ймовірностями
Введемо до розгляду дискретну випадкову величину Х - «число появи події А при пвипробуваннях» і знайдемо закон розподілу цієї випадкової величини. Величина Х може набувати значення
Ймовірність ![]() того, що випадкову величину Х набуде значення x kзнаходиться за формулою Бернуллі
того, що випадкову величину Х набуде значення x kзнаходиться за формулою Бернуллі
Закон розподілу дискретної випадкової величини, який визначається формулою Бернуллі (1), називається біномним законом розподілу. Постійні п і р (q=1-p), що входять у формулу (1) називаються параметрами біномного розподілу.
Назва «біноміальний розподіл» пов'язана з тим, що права частина рівності (1) це загальний член розкладання бінома Ньютона, тобто.
(2)
А оскільки p+q=1, то права частина рівності (2) дорівнює 1
Це означає, що
 (4)
(4)
У рівності (3) перший член q nу правій частині означає ймовірність того, що в пвипробуваннях подія А не з'явиться жодного разу, другий член ![]() ймовірність того, що подія А з'явиться один раз, третій член - ймовірність, що подія А з'явиться двічі і нарешті останній член р п- ймовірність того, що подія А з'явиться рівно празів.
ймовірність того, що подія А з'явиться один раз, третій член - ймовірність, що подія А з'явиться двічі і нарешті останній член р п- ймовірність того, що подія А з'явиться рівно празів.
Біноміальний закон розподілу дискретної випадкової величини подають у вигляді таблиці:
| Х | 0 | 1 | … | k | … | n |
| Р | q n | … | … | р п |
Основні числові характеристики біномного розподілу:
1) математичне очікування ![]() (5)
(5)
2) дисперсія ![]() (6)
(6)
3) середнє квадратичне відхилення ![]() (7)
(7)
4) найімовірніше число поява події k 0- це число якому при заданому пвідповідає максимальна біномна ймовірність
При заданих пі рце число визначається нерівностями
![]() (8)
(8)
якщо число пр+рне є цілим, то k 0дорівнює цілій частині цього числа, якщо ж пр+р- ціле число, то k 0має два значення
Біноміальний закон розподілу ймовірностей застосовується в теорії стрільби, теорії та практики статистичного контролю якості продукції, теорії масового обслуговування, теорії надійності і т.д. Цей закон може застосовуватися у всіх випадках, коли є послідовність незалежних випробувань.
Приклад 1:Перевіркою якості встановлено, що з кожних 100 приладів немає дефектів 90 штук у середньому. Скласти біноміальний закон розподілу ймовірностей числа якісних приладів із придбаних навмання 4.
Рішення:Подія А - поява якого перевіряється це - «придбаний навмання прилад якісний». За умовою завдання основні параметри біномного розподілу:
Випадкова величина Х - число якісних приладів із взятих 4, означає значення Х -Знайдемо ймовірність значень Х за формулою (1):

Таким чином, закон розподілу величини Х - кількість якісних приладів із взятих 4:
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Для перевірки правильності побудови розподілу перевіримо, чому дорівнює сума ймовірностей
Відповідь:Закон розподілу
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Приклад 2:Застосовуваний метод лікування призводить до одужання у 95% випадків. П'ятеро хворих застосовували цей метод. Знайти найбільш імовірне число одужали, а так само числові характеристики випадкової величини Х - число одужали з 5 хворих, що застосовували даний метод.
Теорія ймовірності незримо є у нашому житті. Ми не звертаємо на це уваги, але кожна подія у нашому житті має ту чи іншу ймовірність. Беручи до уваги безліч варіантів розвитку подій, нам стає необхідним визначати найімовірніші і найменш ймовірні з них. Найбільш зручно аналізувати такі імовірнісні дані графічно. У цьому може допомогти розподіл. Біноміальне - одне з найлегших і найточніших.
Перш ніж перейти безпосередньо до математики та теорії ймовірності, розберемося з тим, хто ж перший вигадав такий вид розподілу та яка історія розвитку математичного апарату для цього поняття.
Історія
Поняття ймовірності відоме ще з давніх часів. Однак давні математики не надавали їй особливо значення і змогли закласти тільки основи для теорії, що згодом стала теорією ймовірності. Вони створили деякі комбінаторні методи, які сильно допомогли тим, хто пізніше створив та розвинув саму теорію.
У другій половині сімнадцятого століття почалося формування основних понять та методів теорії ймовірності. Було введено визначення випадкових величин, способи обчислення ймовірності простих та деяких складних незалежних та залежних подій. Продиктований такий інтерес до випадкових величин та ймовірностей був азартними іграми: кожна людина хотіла знати, які у неї шанси перемогти у грі.
Наступним етапом стало застосування теорії ймовірності методів математичного аналізу. Цим зайнялися визначні математики, такі як Лаплас, Гаусс, Пуассон і Бернуллі. Саме вони просунули цю галузь математики нового рівня. Саме Джеймс Бернуллі відкрив біномний закон розподілу. До речі, як ми пізніше з'ясуємо, на основі цього відкриття було зроблено ще кілька, які дозволили створити закон нормального розподілу та ще багато інших.
Зараз, перш ніж почати описувати розподіл біномний, ми трохи освіжимо в пам'яті поняття теорії ймовірностей, напевно вже забуті зі шкільної лави.
Основи теорії ймовірностей
Розглянемо такі системи, в результаті дії яких можливі лише два результати: "успіх" і "не успіх". Це легко зрозуміти на прикладі: ми підкидаємо монетку, загадавши те, що випаде решка. Імовірності кожної з можливих подій (випаде решка – "успіх", випаде орел – "не успіх") дорівнюють 50 відсоткам при ідеальному балансуванні монети та відсутності інших факторів, які можуть вплинути на експеримент.
Це була найпростіша подія. Але бувають ще й складні системи, в яких виконуються послідовні дії, і ймовірність результатів цих дій відрізнятимуться. Наприклад, розглянемо таку систему: у коробці, вміст якої ми не можемо розглянути, лежать шість абсолютно однакових кульок, три пари синього, червоного та білого кольорів. Ми повинні дістати навмання кілька кульок. Відповідно, витягнувши першою одну з білих кульок, ми зменшимо в рази ймовірність того, що наступним нам теж трапиться біла кулька. Відбувається це тому, що змінюється кількість об'єктів у системі.
У наступному розділі розглянемо складніші математичні поняття, що впритул підводять нас до того, що означають слова "нормальний розподіл", "біноміальний розподіл" тощо.

Елементи математичної статистики
У статистиці, яка є однією з сфер застосування теорії ймовірностей, існує безліч прикладів, коли дані для аналізу дано не в явному вигляді. Тобто не в чисельному, а у вигляді поділу за ознаками, наприклад, за статевими. Для того, щоб застосувати до таких даних математичний апарат та зробити з отриманих результатів якісь висновки, потрібно перевести вихідні дані до числового формату. Як правило, для здійснення цього позитивного результату надають значення 1, а негативному - 0. Таким чином, ми отримуємо статистичні дані, які можна піддати аналізу за допомогою математичних методів.
Наступний крок у розумінні того, що таке біномний розподіл випадкової величини, - це визначення дисперсії випадкової величини та математичного очікування. Про це поговоримо у наступному розділі.

Математичне очікування
Насправді зрозуміти, що таке математичне очікування, нескладно. Розглянемо систему, де існує багато різних подій зі своїми різними ймовірностями. Математичним очікуванням називатиметься величина, що дорівнює сумі творів значень цих подій (а математичному вигляді, про який ми говорили в минулому розділі) на ймовірності їх здійснення.
Математичне очікування біномного розподілу розраховується за тією ж схемою: ми беремо значення випадкової величини, множимо його на ймовірність позитивного результату, а потім підсумовуємо отримані дані для всіх величин. Дуже зручно уявити ці дані графічно - краще сприймається різниця між математичними очікуваннями різних величин.
У наступному розділі ми розповімо вам трохи про інше поняття – дисперсію випадкової величини. Воно теж тісно пов'язане з таким поняттям, як біномний розподіл ймовірностей, і є його характеристикою.

Дисперсія біномного розподілу
Ця величина тісно пов'язана з попередньою та також характеризує розподіл статистичних даних. Вона являє собою середній квадрат відхилень значень від їхнього математичного очікування. Тобто дисперсія випадкової величини - це сума квадратів різниць між значенням випадкової величини та її математичним очікуванням, помножена на ймовірність цієї події.
Загалом це все, що нам потрібно знати про дисперсію для розуміння того, що таке біномне розподіл ймовірностей. Тепер перейдемо безпосередньо до нашої теми. А саме до того, що криється за таким на вигляд досить складним словосполученням "біноміальний закон розподілу".

Біноміальний розподіл
Розберемося для початку, чому ж цей розподіл биноміальний. Воно походить від слова "біном". Можливо, ви чули про біном Ньютона - таку формулу, за допомогою якої можна розкласти суму двох будь-яких чисел a і b будь-якою невід'ємною мірою n.
Як ви, напевно, вже здогадалися, формула бінома Ньютона та формула біномного розподілу – це практично однакові формули. За тим лише винятком, що друга має прикладне значення для конкретних величин, а перша - лише загальний математичний інструмент, застосування якого практично можуть бути різні.
Формули розподілу
Функція біномного розподілу може бути записана у вигляді суми наступних членів:
(n!/(n-k)!k!)*p k *q n-k
Тут n - число незалежних випадкових експериментів, p - число вдалих наслідків, q - число невдалих наслідків, k - номер експерименту (може приймати значення від 0 до n),! - позначення факторіалу, такої функції числа, значення якої дорівнює добутку всіх чисел, що йдуть до неї (наприклад, для числа 4: 4!=1*2*3*4=24).
Крім цього, функція біномного розподілу може бути записана у вигляді неповної бета-функції. Однак це вже складніше визначення, яке використовується лише при вирішенні складних статистичних завдань.
Біноміальний розподіл, приклади якого ми розглянули вище, - один із найпростіших видів розподілів у теорії ймовірностей. Існує також нормальний розподіл, що є одним із видів біномного. Воно використовується найчастіше, і найпростіше у розрахунках. Буває також розподіл Бернуллі, розподіл Пуассон, умовний розподіл. Всі вони характеризують графічно області ймовірності того чи іншого процесу за різних умов.
У наступному розділі розглянемо аспекти застосування цього математичного апарату в реальному житті. На перший погляд, звичайно, здається, що це чергова математична штука, яка, як завжди, не знаходить застосування у реальному житті, і взагалі не потрібна нікому, окрім самих математиків. Однак, це далеко не так. Адже всі види розподілів та їх графічні уявлення були створені виключно під практичні цілі, а не як забаганки вчених.

Застосування
Безумовно, найважливіше застосування розподілу знаходять у статистиці, адже там потрібен комплексний аналіз множини даних. Як показує практика, дуже багато масивів даних мають приблизно однакові розподіли величин: критичні області дуже низьких і дуже високих величин, як правило, містять менше елементів, ніж середні значення.
Аналіз великих масивів даних потрібно у статистиці. Він незамінний, наприклад, у фізичній хімії. У цій науці він використовується визначення багатьох величин, пов'язані з випадковими коливаннями і переміщеннями атомів і молекул.
У наступному розділі розберемося, наскільки важливим є застосування таких статистичних понять, як біномне розподіл випадкової величини у повсякденному житті для нас із вами.

Навіщо мені це треба?
Багато хто ставить собі таке питання, коли справа стосується математики. А між іншим, математика недарма називається царицею наук. Вона є основою фізики, хімії, біології, економіки, і в кожній з цих наук застосовується в тому числі і будь-який розподіл: чи це дискретний біномний розподіл, чи нормальний, не важливо. І якщо ми краще придивимося до навколишнього світу, то побачимо, що математика застосовується скрізь: у повсякденному житті, на роботі, і навіть людські відносини можна представити у вигляді статистичних даних і провести їх аналіз (так, до речі, і роблять ті, хто працюють у спеціальних організаціях, які займаються збиранням інформації).
Зараз поговоримо трохи про те, що ж робити, якщо вам потрібно знати на цю тему набагато більше, ніж те, що ми виклали в цій статті.
Та інформація, яку ми дали у цій статті, далеко не повна. Існує безліч нюансів щодо того, яку форму може набувати розподіл. Біноміальний розподіл, як ми вже з'ясували, є одним з основних видів, на якому ґрунтується вся математична статистика та теорія ймовірностей.
Якщо вам стало цікаво, чи у зв'язку з вашою роботою вам потрібно знати на цю тему набагато більше, потрібно буде вивчити спеціалізовану літературу. Почати слід з університетського курсу математичного аналізу та дійти там до розділу теорії ймовірностей. Також знадобляться знання в області рядів, адже біномний розподіл ймовірностей - це ні що інше, як низка послідовних членів.
Висновок
Перш ніж закінчити статтю, ми хотіли б розповісти ще одну цікаву річ. Вона стосується безпосередньо теми нашої статті та всієї математики загалом.
Багато людей стверджують, що математика - марна наука, і ніщо з того, що вони проходили в школі, їм не знадобилося. Але знання ніколи не буває зайвим, і якщо вам щось не знадобилося в житті, значить, ви просто цього не пам'ятаєте. Якщо у вас є знання, вони можуть вам допомогти, але якщо їх немає, то допомоги від них чекати не доводиться.
Отже, ми розглянули поняття біномного розподілу і всі пов'язані з ним визначення і поговорили про те, як це застосовується в нашому з вами житті.
- (binomial distribution) Розподіл, що дозволяє розрахувати ймовірність настання якоїсь випадкової події, отриманої в результаті спостережень низки незалежних подій, якщо ймовірність наступу, що становлять його елементарні… Економічний словник
- (розподіл Бернуллі) розподіл ймовірностей числа появ певної події при повторних незалежних випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює p(0 p 1). Саме число? появ цієї події є… … Великий Енциклопедичний словник
біномний розподіл- - Тематики електрозв'язок, основні поняття EN binomial distribution …
- (розподіл Бернуллі), розподіл ймовірностей числа появ певної події при повторних незалежних випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює р (0≤р≤1). Саме, кількість μ появи цієї події… … Енциклопедичний словник
біномний розподіл– 1.49. біноміальний розподіл Розподіл ймовірностей дискретної випадкової величини X, що приймає будь-які цілі значення від 0 до n, таке, що при х = 0, 1, 2, ..., n і параметрах n = 1, 2, ... і 0< p < 1, где Источник … Словник-довідник термінів нормативно-технічної документації
Розподіл Бернуллі, розподіл ймовірностей випадкової величини X, що приймає цілі значення з ймовірностями відповідно (біноміальний коефіцієнт; р параметр Б. р., наз. ймовірністю позитивного результату, що приймає значення … Математична енциклопедія
Розподіл ймовірностей кількості появ певної події при повторних незалежних випробуваннях. Якщо при кожному випробуванні ймовірність появи події дорівнює р, причому 0 ≤ p ≤ 1, то число μ появи цієї події при n незалежних… … Велика Радянська Енциклопедія
- (розподіл Бернуллі), розподіл ймовірностей числа появ нек рого події при повторних незалежних випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні дорівнює р (0<или = p < или = 1). Именно, число м появлений … Природознавство. Енциклопедичний словник
Біноміальний розподіл ймовірностей- (binomial distribution) Розподіл, який спостерігається у випадках, коли результат кожного незалежного експерименту (статистичного спостереження) приймає одне з двох можливих значень: перемога чи поразка, включення чи виняток, плюс чи … Економіко-математичний словник
біномне розподіл ймовірностей- Розподіл, який спостерігається у випадках, коли результат кожного незалежного експерименту (статистичного спостереження) набуває одного з двох можливих значень: перемога чи поразка, включення чи виняток, плюс чи мінус, 0 чи 1. Тобто… … Довідник технічного перекладача
Книги
- Теорія ймовірностей та математична статистика у завданнях. Більше 360 завдань та вправ, Д. А. Борзих. У запропонованому посібнику містяться завдання різного рівня складності. Проте основний акцент зроблено на завдання середньої складності. Це зроблено навмисно для того, щоб спонукати студентів до…
- Теорія ймовірностей та математична статистика у завданнях Більше 360 завдань та вправ, Борзих Д.. У запропонованому посібнику містяться завдання різного рівня складності. Проте основний акцент зроблено на завдання середньої складності. Це зроблено навмисно для того, щоб спонукати студентів до…
Розділ 7.
Конкретні закони розподілу випадкових величин
Види законів розподілу дискретних випадкових величин
Нехай дискретна випадкова величина може набувати значення х 1 , х 2 , …, х n, …. Імовірності цих значень можуть бути обчислені за різними формулами, наприклад, за допомогою основних теорем теорії ймовірностей, формули Бернуллі або інших формул. Для деяких із цих формул закон розподілу має свою назву.
Найбільш поширеними законами розподілу дискретної випадкової величини є біноміальний, геометричний, гіпергеометричний, закон розподілу Пуассона.
Біноміальний закон розподілу
Нехай проводиться nнезалежних випробувань, у кожному з яких може з'явитися чи не з'явитися подія А. Імовірність появи цієї події в кожному одиничному випробуванні постійна, не залежить від номера випробування і дорівнює р=Р(А). Звідси ймовірність не появи події Ау кожному випробуванні також постійна і рівна q=1–р. Розглянемо випадкову величину Хрівну числу події Ав nвипробуваннях. Очевидно, що значення цієї величини дорівнюють
х 1 = 0 - подія Ав nвипробуваннях не з'явилося;
х 2 = 1 - подія Ав nвипробування з'явилося один раз;
х 3 = 2 - подія Ав nвипробування з'явилося двічі;
…………………………………………………………..
х n +1 = n– подія Ав nвипробуваннях з'явилося все nразів.
Імовірності цих значень можуть бути обчислені за формулою Бернуллі (4.1):
де до=0, 1, 2, …,n .
Біноміальним законом розподілу Х, що дорівнює кількості успіхів у nвипробуваннях Бернуллі, з ймовірністю успіху р.
Отже, дискретна випадкова величина має біномний розподіл (або розподілена за біноміальним законом), якщо її можливі значення 0, 1, 2, …, n, А відповідні ймовірності обчислюються за формулою (7.1).
Біноміальний розподіл залежить від двох параметрів рі n.
Ряд розподілу випадкової величини, розподіленої за біноміальним законом, має вигляд:
| Х | … | k | … | n | ||
| Р | | … | … | |
приклад 7.1 . Здійснюється три незалежні постріли по мішені. Імовірність влучення при кожному пострілі дорівнює 0,4. Випадкова величина Х- Число попадань в ціль. Побудувати її низку розподілу.
Рішення. Можливими значеннями випадкової величини Хє х 1 =0; х 2 =1; х 3 =2; х 4 =3. Знайдемо відповідні можливості, використовуючи формулу Бернуллі. Неважко показати, що застосування цієї формули тут цілком виправдане. Зазначимо, що ймовірність не влучення в ціль при одному пострілі дорівнюватиме 1-0,4 = 0,6. Отримаємо

Ряд розподілу має такий вигляд:
| Х | ||||
| Р | 0,216 | 0,432 | 0,288 | 0,064 |
Неважко перевірити, що сума всіх ймовірностей дорівнює 1. Сама випадкова величина Хрозподілено за біноміальним законом. ■
Знайдемо математичне очікування та дисперсію випадкової величини, розподіленої за біноміальним законом.
При рішенні прикладу 6.5 було показано, що математичне очікування кількості події Ав nнезалежних випробувань, якщо ймовірність появи Ау кожному випробуванні постійна і рівна р, одно n· р
У цьому прикладі використовувалася випадкова величина, розподілена за біноміальним законом. Тому рішення прикладу 6.5 по суті є доказом наступної теореми.
Теорема 7.1.Математичне очікування дискретної випадкової величини, розподіленої за біноміальним законом, дорівнює добутку числа випробувань на можливість " успіху " , тобто. М(Х)=n· нар.
Теорема 7.2.Дисперсія дискретної випадкової величини, розподіленої по биномиальному закону, дорівнює добутку числа випробувань на ймовірність " успіху " і ймовірність " невдачі " , тобто. D(Х)=nрq.
Асиметрія та ексцес випадкової величини, розподіленої за біноміальним законом, визначаються за формулами
Ці формули можна отримати, скориставшись поняттям початкових та центральних моментів.
Біноміальний закон розподілу є основою багатьох реальних ситуацій. При великих значеннях nбіномний розподіл може бути апроксимований за допомогою інших розподілів, зокрема за допомогою розподілу Пуассона.
Розподіл Пуассона
Нехай є nвипробувань Бернуллі, при цьому кількість випробувань nдосить велике. Раніше було показано, що в цьому випадку (якщо до того ж ймовірність рподії Адуже мала) для знаходження ймовірності того, що подія Аз'явитися траз у випробуваннях можна скористатися формулою Пуассона (4.9). Якщо випадкова величина Хозначає кількість появи події Ав nвипробуваннях Бернуллі, то ймовірність того, що Хнабуде значення kможе бути обчислена за формулою
 , (7.2)
, (7.2)
де λ = nр.
Законом розподілу Пуассонаназивається розподіл дискретної випадкової величини Х, для якої можливими значеннями є цілі невід'ємні числа, а ймовірності р тцих значень перебувають за формулою (7.2).
Величина λ = nрназивається параметромрозподілу Пуассона.
Випадкова величина, розподілена за законом Пуассона, може набувати безліч значень. Так як для цього розподілу ймовірність рПоява події в кожному випробуванні мала, то цей розподіл іноді називають законом рідкісних явищ.
Ряд розподілу випадкової величини, розподіленої згідно із законом Пуассона, має вигляд
| Х | … | т | … | ||||
| Р | … | … |
Неважко переконатися, що сума ймовірностей другого рядка дорівнює 1. Для цього необхідно згадати, що функцію можна розкласти в рядок Маклорена, який сходиться для будь-якого х. В даному випадку маємо
 . (7.3)
. (7.3)
Як зазначалося, закон Пуассона у певних граничних випадках замінює биномиальный закон. Як приклад можна навести випадкову величину Хзначення якої рівні кількості збоїв за певний проміжок часу при багаторазовому застосуванні технічного пристрою. У цьому передбачається, що це пристрій високої надійності, тобто. ймовірність збою при одному застосуванні дуже мала.
Крім таких граничних випадків, на практиці трапляються випадкові величини, розподілені за законом Пуассона, не пов'язані з біномним розподілом. Наприклад, розподіл Пуассона часто використовується тоді, коли мають справу з кількістю подій, що з'являються в проміжку часу (кількість надходжень викликів на телефонну станцію протягом години, кількість машин, що прибули на автомийку протягом доби, кількість зупинок верстатів на тиждень і т.п. .). Всі ці події повинні утворювати так званий потік подій, який є одним з основних понять теорії масового обслуговування. Параметр λ характеризує середню інтенсивність потоку подій.
приклад 7.2 . На факультеті налічується 500 студентів. Якою є ймовірність того, що 1 вересня є днем народження для трьох студентів даного факультету?
Рішення . Оскільки кількість студентів n=500 досить велике і р- Імовірність народиться першого вересня будь-якому зі студентів дорівнює, тобто. досить мала, можна вважати, що випадкова величина Х– кількість студентів, що народилися першого вересня, розподілено згідно із законом Пуассона з параметром λ = np= =1,36986. Тоді, за формулою (7.2) отримаємо
Теорема 7.3.Нехай випадкова величина Хрозподілено згідно із законом Пуассона. Тоді її математичне очікування та дисперсія дорівнюють один одному і дорівнюють значенню параметра λ , тобто. M(X) = D(X) = λ = np.
Доведення.За визначенням математичного очікування, використовуючи формулу (7.3) та ряд розподілу випадкової величини, розподіленої за законом Пуассона, отримаємо
Перш ніж знайти дисперсію, знайдемо спочатку математичне очікування квадрата аналізованої випадкової величини. Отримуємо

Звідси, за визначенням дисперсії, отримуємо
Теорему доведено.
Застосовуючи поняття початкових та центральних моментів, можна показати, що для випадкової величини, розподіленої за законом Пуассона, коефіцієнти асиметрії та ексцесу визначаються за формулами
Неважко зрозуміти, що, оскільки за змістом параметр λ = npпозитивний, то у випадкової величини, розподіленої за законом Пуассона, завжди позитивні і асиметрія та ексцес.
Біноміальний розподіл - один з найважливіших розподілів ймовірностей випадкової величини, що дискретно змінюється. Біноміальним розподілом називається розподіл ймовірностей числа mнастання події Ав nвзаємно незалежні спостереження. Часто подія Аназивають "успіхом" спостереження, а протилежна йому подія - "неуспіхом", але це позначення дуже умовне.
Умови біномного розподілу:
- загалом проведено nвипробувань, у яких подія Аможе наступити чи наступити;
- подія Ау кожному з випробувань може наступити з однією і тією самою ймовірністю p;
- випробування є взаємно незалежними.
Імовірність того, що в nвипробуваннях подія Анастане саме mраз, можна обчислити за формулою Бернуллі:
![]()
де p- ймовірність настання події А;
q = 1 - p- Імовірність настання протилежної події.
Розберемося, чому біномний розподіл описаним вище чином пов'язаний з формулою Бернуллі . Подія - кількість успіхів при nвипробуваннях розпадається на ряд варіантів, у кожному з яких успіх досягається в mвипробуваннях, а неуспіх - у n - mвипробуваннях. Розглянемо один із таких варіантів - B1 . За правилом складання ймовірностей примножуємо ймовірності протилежних подій:
![]() ,
,
а якщо позначимо q = 1 - p, то
![]() .
.
Таку ж ймовірність матиме будь-який інший варіант, у якому mуспіхів та n - mнеуспіхів. Число таких варіантів дорівнює - числу способів, якими можна з nвипробувань отримати mуспіхів.
Сума ймовірностей усіх mчисел настання події А(чисел від 0 до n) дорівнює одиниці:
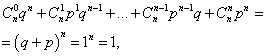
де кожен доданок являє собою доданок бінома Ньютона. Тому розподіл, що розглядається, і називається біноміальним розподілом.
Насправді часто необхідно обчислювати ймовірності " трохи більше mуспіхів у nвипробуваннях" або "не менше mуспіхів у nвипробуваннях". Для цього використовуються наступні формули.
Інтегральну функцію, тобто ймовірність F(m) того, що в nспостереженнях подія Анастане не більше mраз, Можна обчислити за формулою:
В свою чергу ймовірність F(≥m) того, що в nспостереженнях подія Анастане не менше mраз, обчислюється за такою формулою:
Іноді буває зручніше обчислювати ймовірність того, що в nспостереженнях подія Анастане не більше mраз, через ймовірність протилежної події:
![]() .
.
Який із формул користуватися, залежить від того, в якій із них сума містить менше доданків.
Характеристики біномного розподілу обчислюються за такими формулами .
Математичне очікування: .
Дисперсія: .
Середньоквадратичне відхилення: .
Біноміальний розподіл та розрахунки в MS Excel
Імовірність біномного розподілу P n ( m) та значення інтегральної функції F(m) можна обчислити за допомогою функції MS Excel БІНОМ.РАСП. Вікно для відповідного розрахунку показано нижче (для збільшення натиснути лівою кнопкою миші).

MS Excel вимагає ввести такі дані:
- кількість успіхів;
- кількість випробувань;
- ймовірність успіху;
- інтегральна – логічне значення: 0 – якщо потрібно обчислити ймовірність P n ( m) і 1 - якщо ймовірність F(m).
приклад 1.Менеджер фірми узагальнив інформацію про кількість проданих протягом останніх 100 днів фотокамер. У таблиці узагальнено інформацію та розраховано ймовірність того, що в день буде продано певну кількість фотокамер.
День завершено із прибутком, якщо продано 13 або більше фотокамер. Імовірність, що день буде відпрацьовано із прибутком:
![]()
Імовірність того, що день буде відпрацьовано без прибутку:

Нехай ймовірність того, що день відпрацьований з прибутком, є постійною і дорівнює 0,61 і кількість проданих в день фотокамер не залежить від дня. Тоді можна використовувати біномний розподіл, де подія А- день буде відпрацьовано із прибутком, - без прибутку.
Імовірність того, що з 6 днів усі будуть відпрацьовані із прибутком:
![]() .
.
Той самий результат отримаємо, використовуючи функцію MS Excel БІНОМ.РАСП (значення інтегральної величини - 0):
P 6 (6 ) = БІНОМ.РАСП(6; 6; 0,61; 0) = 0,052.
Імовірність того, що з 6 днів 4 і більше днів будуть відпрацьовані із прибутком:
де ![]() ,
,
![]() ,
,
Використовуючи функцію MS Excel БІНОМ.РАСП, обчислимо ймовірність того, що з 6 днів не більше 3 днів буде завершено з прибутком (значення інтегральної величини - 1):
P 6 (≤3 ) = БІНОМ.РАСП(3; 6; 0,61; 1) = 0,435.
Імовірність того, що з 6 днів усі будуть відпрацьовані зі збитками:
![]() ,
,
Той самий показник обчислимо, використовуючи функцію MS Excel БІНОМ.РАСП:
P 6 (0 ) = БІНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.
Вирішити завдання самостійно, а потім переглянути рішення
приклад 2.В урні 2 білі кулі та 3 чорні. З урни виймають кулю, встановлюють колір та кладуть назад. Спробу повторюють 5 разів. Число появи білих куль - дискретна випадкова величина X, Розподілена за біноміальним законом. Скласти закон розподілу випадкової величини. Визначити моду, математичне очікування та дисперсію.
Продовжуємо вирішувати завдання разом
приклад 3.З кур'єрської служби вирушили на об'єкти n= 5 кур'єрів. Кожен кур'єр з ймовірністю p= 0,3 незалежно від інших спізнюється об'єкт. Дискретна випадкова величина X- Кількість кур'єрів, що запізнилися. Побудувати низку розподілу це випадкової величини. Знайти її математичне очікування, дисперсію, середнє відхилення. Знайти ймовірність того, що на об'єкти запізняться щонайменше два кур'єри.



