Чому дорівнює модуль x 1. Розв'язання рівнянь із модулем

Серед прикладів на модулічасто зустрічаються рівняння, де потрібно знайти коріння модуля в модулі, тобто рівняння виду
||a*x-b|-c|=k*x+m.
Якщо k=0 , тобто права сторона дорівнює постійній (m), то простіше шукати рішення рівняння із модулями графічно.Нижче наведено методику розкриття подвійних модулівна поширених на практику прикладах. Добре розберіть алгоритм обчислення рівнянь з модулями, щоб не мати проблем на контрольних тестах і просто знати.

приклад 1. Розв'язати рівняння модуль у модулі |3|x|-5|=-2x-2.
Рішення: Завжди починають розкривати рівняння із внутрішнього модуля
|x|=0 <->x = 0.
У точці x=0 рівняння з модулем поділяється на 2 .
При x< 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
При x>0 або одно, розкриваючи модуль отримаємо
|3x-5|=-2x-2.
Розв'яжемо рівняннядля негативних змінних (x< 0) . Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).

З першого рівняння отримаємо що рішення має перевищувати (-1) , тобто.

Це обмеження повністю належить області, у якій вирішуємо. Перенесемо змінні та постійні по різні сторони рівності у першій та другій системі

і знайдемо рішення


Обидва значення належать проміжку, що розглядається, тобто є корінням.
Розглянемо рівняння з модулями при позитивних змінних
|3x-5|=-2x-2.
Розкриваючи модуль отримаємо дві системи рівнянь

З першого рівняння, яке є загальним для двох систем, отримаємо знайому умову

що у перетині з безліччю, у якому шукаємо рішення дає порожнє безліч (немає точок перетину). Отже єдиним корінням модуля з модулем є значення
x=-3; x=-1,4.

приклад 2. Розв'язати рівняння із модулем ||x-1|-2|=3x-4.
Рішення: Почнемо з розкриття внутрішнього модуля
|x-1|=0 <=>x=1.
Підмодульна функція змінює знак одиниці. При менших значеннях вона негативна, при більших – позитивна. Відповідно до цього при розкритті внутрішнього модуля отримаємо два рівняння з модулем
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Обов'язково перевіряємо праву сторону рівняння з модулем, вона повинна бути більшою за нуль.
3x-4>=0 -> x> = 4/3.
Це означає, що перше з рівнянь немає необхідності вирішувати, оскільки воно виписане для x< 1, что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4або x-3 = 4-3x;
4-3=3x-x або x+3x=4+3;
2x = 1 або 4x = 7;
x=1/2 чи x=7/4.
Набули два значення, перше з яких відкидаємо, оскільки не належить потрібному інтервалу. Остаточно рівняння має одне рішення x=7/4.

приклад 3. Розв'язати рівняння з модулем ||2x-5|-1|=x+3.
Рішення: Розкриємо внутрішній модуль
| 2x-5 | = 0 <=>x = 5/2 = 2,5.
Крапка x=2,5 розбиває числову вісь на два інтервали. Відповідно, підмодульна функціязмінює знак під час переходу через 2,5. Випишемо умову рішення з правого боку рівняння з модулем.
x+3>=0 -> x>=-3.
Отже, рішенням можуть бути значення, не менше (-3) . Розкриємо модуль для негативного значення внутрішнього модуля
|-(2x-5)-1|=x+3;
-2x +4 | = x +3.
Цей модуль також при розкритті дасть 2 рівняння
-2x+4=x+3 або 2x-4=x+3;
2x+x=4-3 або 2x-x=3+4;
3x=1; x=1/3 чи x=7 .
Значення x=7 відкидаємо, оскільки шукали рішення на проміжку [-3;2,5]. Тепер розкриваємо внутрішній модуль для x>2,5. Отримаємо рівняння з одним модулем
| 2x-5-1 | = x +3;
| 2x-6 | = x +3.
При розкритті модуля отримаємо наступні лінійні рівняння
-2x+6=x+3 або 2x-6=x+3;
2x+x=6-3 або 2x-x=3+6;
3x = 3; x=1 або x=9.
Перше значення x=1 не задовольняє умову x>2,5. Так що на цьому інтервалі маємо один корінь рівняння з модулем x=9, а всього їх два (x=1/3). Підстановкою можна перевіряти правильність виконаних обчислень
Відповідь: x = 1/3; x = 9.

приклад 4. Знайти рішення подвійного модуля | 3x-1 | -5 | = 2x-3.
Рішення: Розкриємо внутрішній модуль рівняння
|3x-1|=0 <=>x = 1/3.
Точка x=2,5 ділить числову вісь на два інтервали, а задане рівняння на два випадки. Записуємо умову на рішення, виходячи з виду рівняння з правого боку
2x-3>=0 -> x> = 3/2 = 1,5.
Звідси випливає, що нас цікавлять значення >=1,5. Таким чином модульне рівняннярозглядаємо на двох інтервалах
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Отриманий модуль при розкритті поділяється на 2 рівняння
-3x-4=2x-3 або 3x+4=2x-3;
2x+3x=-4+3 або 3x-2x=-3-4;
5x=-1; x=-1/5 або x=-7.
Обидва значення не потрапляють у проміжок , тобто є рішеннями рівняння з модулями. Далі розкриємо модуль для x> 2,5. Отримаємо наступне рівняння
| 3x-1-5 | = 2x-3;
| 3x-6 | = 2x-3.
Розкриваючи модуль, отримаємо 2 лінійні рівняння
3x-6=2x-3 або - (3x-6) = 2x-3;
3x-2x=-3+6або 2x+3x=6+3;
x=3 чи 5x=9; x = 9/5 = 1,8.
Друге значення зі знайдених відповідає умові x>2,5 , його ми відкидаємо.
Нарешті маємо один корінь рівняння із модулями x=3 .
Виконуємо перевірку
||3*3-1|-5|=2*3-3 3=3 .
Корінь рівняння з модулем правильно обчислено.
Відповідь: x = 1/3; x = 9.

Не ми вибираємо математикусвоєю професією, а вона нас обирає.

Російський математик Ю.І. Манін

Рівняння з модулем

Найбільш складними завданнями шкільної математики є рівняння, що містять змінні під знаком модуля. Для успішного розв'язання таких рівнянь необхідно знати визначення та основні властивості модуля. Звичайно, що учні повинні мати навички розв'язання рівнянь такого типу.

Основні поняття та властивості

Модуль (абсолютна величина) дійсного числапозначається і визначається так:

До простих властивостей модуля належать такі співвідношення:

Зазначимо, що останні дві властивості справедливі для будь-якого парного ступеня.

Крім того, якщо, де, то і

Більш складні властивості модуля, які можна ефективно використовувати при вирішенні рівнянь із модулями, формулюються за допомогою наступних теорем:

Теорема 1.Для будь-яких аналітичних функційі справедлива нерівність

Теорема 2.Рівність рівнозначна нерівності.

Теорема 3.Рівність рівносильно нерівності.

Розглянемо типові приклади розв'язання задач на тему «Рівняння, що містять змінні під знаком модуля».

Розв'язання рівнянь із модулем

Найбільш поширеним у шкільній математиці методом розв'язання рівнянь із модулем є метод, заснований на розкритті модулів. Цей метод є універсальним, однак у загальному випадку його застосування може призвести до громіздких обчислень. У зв'язку з цим учні повинні знати й інші, більш ефективні методи та прийоми розв'язання таких рівнянь. Зокрема, необхідно мати навички застосування теорем, наведених у цій статті.

приклад 1.Вирішити рівняння . (1)

Рішення. Рівняння (1) вирішуватимемо «класичним» методом – методом розкриття модулів. Для цього розіб'ємо числову вісьточками та на інтервали та розглянемо три випадки.

1. Якщо , то , , , і рівняння (1) набуває вигляду . Звідси випливає. Однак тут , тому знайдене значення не є коренем рівняння (1).

2. Якщо , то з рівняння (1) отримуємоабо .

Оскільки , то корінь рівняння (1).

3. Якщо , то рівняння (1) набуває виглядуабо . Відмітимо, що .

Відповідь: , .

При вирішенні наступних рівнянь з модулем активно використовуватимемо властивості модулів з метою підвищення ефективності розв'язання подібних рівнянь.

приклад 2.Вирішити рівняння.

Рішення.Так як і , то з рівняння випливає. В зв'язку з цим , , , і рівняння набуває вигляду. Звідси отримуємо. Однак, тому вихідне рівняння коренів немає.

Відповідь: коріння немає.

приклад 3.Вирішити рівняння.

Рішення.Так як, то. Якщо то , і рівняння набуває вигляду.

Звідси отримуємо.

приклад 4.Вирішити рівняння.

Рішення.Перепишемо рівняння у рівносильному вигляді. (2)

Отримане рівняння відноситься до рівнянь типу.

Беручи до уваги теорему 2, можна стверджувати, що рівняння (2) рівнозначне нерівності. Звідси отримуємо.

Відповідь: .

Приклад 5.Вирішити рівняння .

Рішення. Дане рівняння має вигляд. Тому , згідно з теоремою 3, тут маємо нерівністьабо .

Приклад 6.Вирішити рівняння.

Рішення.Припустимо, що. Так як , то задане рівняння набуває вигляду квадратного рівняння, (3)

де . Оскільки рівняння (3) має єдиний позитивний коріньі то . Звідси отримуємо два корені вихідного рівняння:та .

Приклад 7. Вирішити рівняння. (4)

Рішення. Оскільки рівняннярівносильно сукупності двох рівнянь:і , то при вирішенні рівняння (4) необхідно розглянути два випадки.

1. Якщо , то чи .

Звідси отримуємо , та .

2. Якщо , то чи .

Так як, то.

Відповідь: , , , .

Приклад 8.Вирішити рівняння . (5)

Рішення.Так як і , то . Звідси і з рівняння (5) випливає, як і , тобто. тут маємо систему рівнянь

Однак дана система рівнянь є несумісною.

Відповідь: коріння немає.

Приклад 9. Вирішити рівняння. (6)

Рішення.Якщо позначити, то і з рівняння (6) отримуємо

Або. (7)

Оскільки рівняння (7) має вигляд , це рівняння рівнозначно нерівності . Звідси отримуємо. Так як , то чи .

Відповідь: .

приклад 10.Вирішити рівняння. (8)

Рішення.Відповідно до теореми 1 можна записати

(9)

Беручи до уваги рівняння (8), робимо висновок у тому, що обидві нерівності (9) звертаються до рівності, тобто. має місце система рівнянь

Однак за теоремою 3 наведена вище система рівнянь рівносильна системі нерівностей

(10)

Вирішуючи систему нерівностей (10) отримуємо . Оскільки система нерівностей (10) дорівнює рівнянню (8), то вихідне рівняння має єдиний корінь .

Відповідь: .

Приклад 11. Вирішити рівняння. (11)

Рішення.Нехай і тоді з рівняння (11) випливає рівність .

Звідси випливає, що . Таким чином, тут маємо систему нерівностей

Розв'язанням даної системи нерівностей єта .

Відповідь: , .

приклад 12.Вирішити рівняння. (12)

Рішення. Рівняння (12) вирішуватимемо методом послідовного розкриття модулів. Для цього розглянемо кілька випадків.

1. Якщо, то.

1.1. Якщо , то , .

1.2. Якщо то . Однак, тому у разі рівняння (12) коренів немає.

2. Якщо, то.

2.1. Якщо , то , .

2.2. Якщо, то й.

Відповідь: , , , , .

приклад 13.Вирішити рівняння. (13)

Рішення.Оскільки ліва частина рівняння (13) невід'ємна, то і . У цьому зв'язку і рівняння (13)

набуває вигляду або .

Відомо, що рівняння рівносильно сукупності двох рівняньі , вирішуючи які отримуємо, . Так як , то рівняння (13) має один корінь.

Відповідь: .

приклад 14. Розв'язати систему рівнянь (14)

Рішення.Так як і , то і . Отже, із системи рівнянь (14) отримуємо чотири системи рівнянь:

Коріння наведених вище систем рівнянь є корінням системи рівнянь (14).

Відповідь: ,, , , , , , .

приклад 15. Розв'язати систему рівнянь (15)

Рішення.Так як, то. У цьому зв'язку із системи рівнянь (15) отримуємо дві системи рівнянь

Корінням першої системи рівнянь є і , та якщо з другої системи рівнянь отримуємо і .

Відповідь: , , , .

Приклад 16 Розв'язати систему рівнянь (16)

Рішення.З першого рівняння системи (16) випливає, що .

Оскільки , то . Розглянемо друге рівняння системи. Оскільки, то , і рівняння набуває вигляду, , або .

Якщо підставити значенняу перше рівняння системи (16), то або .

Відповідь: , .

Для більш глибокого вивчення методів розв'язання задач, пов'язаних із розв'язанням рівнянь, містять змінні під знаком модуля, можна порадити навчальні посібники зі списку літератури, що рекомендується.

1. Збірник завдань з математики для вступників у втузи / За ред. М.І. Сканаві. - М.: Світ та Освіта, 2013. - 608 с.

2. Супрун В.П. Математика для старшокласників: завдання підвищеної складності. - М.: КД "Ліброком" / URSS, 2017. - 200 с.

3. Супрун В.П. Математика для старшокласників: нестандартні методи розв'язання задач. - М.: КД "Ліброком" / URSS, 2017. - 296 с.

Залишились питання?

Щоб отримати допомогу репетитора – зареєструйтесь.

сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.

А обчислюється відповідно до таких правил:

Для стислості запису застосовують |а|. Так, |10| = 10; - 1/3 = | 1/3 |; | -100 | =100 і т.д.

Будь-якій величині хвідповідає досить точна величина х|. І значить тотожність у= |х| встановлює уяк деяку функцію аргументу х.

Графікцією функціїпредставлений нижче.

Для x > 0 |x| = x, а для x< 0 |x|= -x; у зв'язку з цим лінія у = | x| при x> 0 поєднана з прямою у = х(бісектриса першого координатного кута), а при х< 0 - с прямой у = -х(бісектриса другого координатного кута).

Окремі рівняннявключають невідомі під знаком модуля.

Довільні приклади таких рівнянь – | х— 1| = 2, |6 — 2х| =3х+ 1 і т.д.

Розв'язання рівняньмістять невідому під знаком модуля базується на тому, що якщо абсолютна величина невідомого числа х дорівнює позитивному числу а, то саме це число х дорівнює або а, або -а.

Наприклад:, якщо | х| = 10, або х=10, або х = -10.

Розглянемо вирішення окремих рівнянь.

Проаналізуємо рішення рівняння х- 1| = 2.

Розкриємо модультоді різниця х- 1 може дорівнювати або + 2, або - 2. Якщо х - 1 = 2, то х= 3; якщо ж х- 1 = - 2, то х= - 1. Робимо підставку і отримуємо, що ці значення задовольняють рівнянню.

Відповідь.Зазначене рівняння має два корені: x 1 = 3, x 2 = - 1.

Проаналізуємо вирішення рівняння | 6 — 2х| = 3х+ 1.

Після розкриття модуляотримуємо: або 6 - 2 х= 3х+ 1, або 6 - 2 х= - (3х+ 1).

В першому випадку х= 1, а в другому х= - 7.

Перевірка.При х= 1 |6 — 2х| = |4| = 4, 3x+ 1 = 4; від суду випливає, х = 1 - коріньданого рівняння.

При x = - 7 |6 — 2x| = |20| = 20, 3x+ 1 = - 20; оскільки 20 ≠ -20, то х= - 7 перестав бути коренем даного рівняння.

Відповідь. Урівняння єдиний корінь: х = 1.

Рівняння такого типу можна вирішувати та графічно.

Так вирішимо, наприклад, графічне рівняння | х- 1| = 2.

Спочатку виконаємо побудову графіка функції у = |x- 1 |. Першим накреслимо графік функції у=х- 1:

Ту частину цього графіка, яка розташована вище за осю хміняти не будемо. Для неї х- 1 > 0 і тому | х-1|=х-1.

Частина графіка, розташована під віссю х, зобразимо симетричнощодо цієї осі. Бо для цієї частини х - 1 < 0 и соответственно |х - 1|= - (х - 1). Утворилася в результаті лінія(суцільна лінія) і буде графіком функціїу = | х—1|.

Ця лінія перетнеться з прямий у= 2 у двох точках: M 1 з абсцисою -1 та М 2 з абсцисою 3. І, відповідно, у рівняння | х- 1 | =2 буде два корені: х 1 = - 1, х 2 = 3.

Модуль — одна з тих речей, про які начебто всі чули, але насправді ніхто нормально не розуміє. Тому сьогодні буде великий урок, присвячений вирішенню рівнянь із модулями.

Відразу скажу: урок буде нескладним. І взагалі модулі взагалі тема відносно нескладна. «Звісно, ​​нескладна! У мене від неї мозок розривається! - скажуть багато учнів, але всі ці розриви мозку відбуваються через те, що у більшості людей у ​​голові не знання, а якась хрень. І мета цього уроку - перетворити хрень на знання.

Трохи теорії

Тож поїхали. Почнемо з найважливішого: що таке модуль? Нагадаю, що модуль числа — це просто те саме число, але взяте без знака «мінус». Тобто, наприклад, $ \ left | -5 \right | = 5 $. Або $ \ left | -129,5 \ right | = 129,5 $.

Ось так просто? Да просто. А чому тоді дорівнює модуль позитивного числа? Тут ще простіше: модуль позитивного числа дорівнює самому цьому числу: $ \ left | 5 \right|=5$; $ \ left | 129,5 \right | = 129,5 $ і т.д.

Виходить цікава річ: різні числа можуть мати той самий модуль. Наприклад: $ \ left | -5 \right|=\left| 5 \right|=5$; $ \ left | -129,5 \right|=\left| 129,5 \ right | = 129,5 $. Неважко помітити, що це числа, у яких модулі однакові: ці числа протилежні. Отже, відзначимо собі, що модулі протилежних чисел рівні:

\[\left| -a \right|=\left| a \right|\]

Ще один важливий факт: модуль ніколи не буває негативним. Яке число ми не взяли — хоч позитивне, хоч негативне — його модуль завжди виявляється позитивним (або в крайньому випадку нулем). Саме тому модуль часто називають абсолютною величиною числа.

Крім того, якщо поєднати визначення модуля для позитивного та негативного числа, то отримаємо глобальне визначення модуля для всіх чисел. А саме: модуль числа дорівнює самому числу, якщо число позитивне (або нуль), або дорівнює протилежному числу, якщо число негативне. Можна записати це у вигляді формули:

Ще є модуль нуля, але він завжди дорівнює нулю. Крім того, нуль — однина, яка не має протилежного.

Таким чином, якщо розглянути функцію $ y = \ left | x \right|$ і спробувати намалювати її графік, то вийде така «галка»:

Графік модуля та приклад розв'язання рівняння

З цієї картинки відразу видно, що $ \ left | -m \right|=\left| m \right|$, а графік модуля ніколи не опускається нижче за осі абсцис. Але це ще не все: червоною лінією відзначена пряма $y=a$, яка при позитивних $a$ дає нам відразу два корені: $((x)_(1))$ і $((x)_(2)) $, але про це ми поговоримо пізніше.

Крім чисто алгебраїчного визначення є геометричне. Припустимо, є дві точки на числовій прямій: $((x)_(1))$ і $((x)_(2))$. І тут вираз $\left| ((x)_(1))-((x)_(2)) \right|$ - це просто відстань між зазначеними точками. Або, якщо завгодно, довжина відрізка, що з'єднує ці точки:

З цього визначення також випливає, що модуль завжди негативний. Але вистачить визначень та теорії — перейдемо до справжніх рівнянь.

Основна формула

Ну гаразд, з визначенням розібралися. Але легше від цього не стало. Як розв'язувати рівняння, що містять цей модуль?

Спокій тільки спокій. Почнемо з найпростіших речей. Розглянемо щось типу такого:

\[\left| x \right|=3\]

Отже, модуль$x$ дорівнює 3. Чому може дорівнювати $x$? Ну, судячи з визначення, нас цілком влаштує $x=3$. Дійсно:

\[\left| 3 \right|=3\]

Чи є інші числа? Кеп ніби натякає, що є. Наприклад, $ x = -3 $ - для нього теж $ \ left | -3 \right | = 3 $, тобто. необхідну рівність виконується.

То, може, якщо пошукати, подумати, ми знайдемо ще числа? А ось обломтеся: більше чисел немає. Рівняння $ \ left | x \right|=3$ має лише два корені: $x=3$ і $x=-3$.

Тепер трохи ускладнимо завдання. Нехай замість змінної $x$ під знаком модуля тусується функція $f\left(x \right)$, а праворуч замість трійки поставимо довільне число $a$. Отримаємо рівняння:

\[\left| f\left(x \right) \right|=a\]

Ну, і як таке вирішувати? Нагадаю: $f\left(x \right)$ - довільна функція, $ a $ - будь-яке число. Тобто. взагалі будь-яке! Наприклад:

\[\left| 2x+1 \right|=5\]

\[\left| 10x-5 \right|=-65\]

Звернімо увагу на друге рівняння. Про нього відразу можна сказати: коріння в нього немає. Чому? Все правильно: тому що в ньому потрібно, щоб модуль дорівнював негативному числу, чого ніколи не буває, оскільки ми вже знаємо, що модуль - число завжди позитивне або в крайньому випадку нуль.

А ось із першим рівнянням все веселіше. Тут два варіанти: або під знаком модуля стоїть позитивний вираз, і тоді $ \ left | 2x+1 \right|=2x+1$, або це вираз все-таки негативне, і тоді $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. У першому випадку наше рівняння перепишеться так:

\[\left| 2x+1 \right|=5\Rightarrow 2x+1=5\]

І раптово виходить, що підмодульний вираз $2x+1$ дійсно позитивний - він дорівнює числу 5. Тобто. ми можемо спокійно вирішувати це рівняння - отриманий корінь буде шматком відповіді:

Особливо недовірливі можуть спробувати підставити знайдений корінь у вихідне рівняння та переконатися, що справді під модулем буде позитивне число.

Тепер розберемо випадок негативного підмодульного виразу:

\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\end(align) \right.\Rightarrow -2x-1=5 \Rightarrow 2x+1=-5\]

Опа! Знову все чітко: ми припустили, що $2x+1 \lt 0$, і в результаті отримали, що $2x+1=-5$ — це вираз менше нуля. Вирішуємо отримане рівняння, при цьому вже точно знаючи, що знайдений корінь нас влаштує:

Разом ми знову отримали дві відповіді: $ x = 2 $ і $ x = 3 $. Так, обсяг обчислень виявився трохи більшим, ніж у зовсім простому рівнянні $ \ left | x \right|=3$, але нічого не змінилося. То, може, існує якийсь універсальний алгоритм?

Так, такий алгоритм існує. І зараз ми його розберемо.

Звільнення від знаку модуля

Нехай нам дано рівняння $ \ left | f\left(x \right) \right|=a$, причому $a\ge 0$ (інакше, як ми вже знаємо, коріння немає). Тоді можна позбавитися знака модуля за таким правилом:

\[\left| f\left(x \right) \right|=a\Rightarrow f\left(x \right)=\pm a\]

Таким чином, наше рівняння із модулем розпадається на два, але вже без модуля. Ось і вся розробка! Спробуємо вирішити кілька рівнянь. Почнемо ось із такого

\[\left| 5x+4 \right|=10\Rightarrow 5x+4=\pm 10\]

Окремо розглянемо, коли праворуч стоїть десятка з плюсом, і окремо коли з мінусом. Маємо:

\[\begin(align)& 5x+4=10\Rightarrow 5x=6\Rightarrow x=\frac(6)(5)=1,2; \&& 5x+4=-10\Rightarrow 5x=-14\Rightarrow x=-\frac(14)(5)=-2,8. \\end(align)\]

От і все! Отримали два корені: $ x = 1,2 $ і $ x = -2,8 $. Все рішення зайняло буквально два рядки.

Ок, не питання, давайте розглянемо щось трохи серйозніше:

\[\left| 7-5x \right|=13\]

Знову відкриваємо модуль з плюсом та мінусом:

\[\begin(align)& 7-5x=13\Rightarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \&& 7-5x=-13\Rightarrow -5x=-20\Rightarrow x=4. \\end(align)\]

Знову кілька рядків — і відповідь готова! Як я й казав, у модулях немає нічого складного. Потрібно лише запам'ятати кілька правил. Тому йдемо далі і приступаємо з справді складнішим завданням.

Випадок змінної правої частини

А тепер розглянемо таке рівняння:

\[\left| 3x-2 \right|=2x\]

Це рівняння принципово відрізняється від попередніх. Чим? А тим, що праворуч від знака рівності стоїть вираз $2x$ — і ми не можемо заздалегідь знати, чи воно позитивне, чи негативне.

Як бути у такому разі? По-перше, треба раз і назавжди зрозуміти, що якщо права частина рівняння виявиться негативною, то рівняння не матиме коріння— ми вже знаємо, що модуль не може дорівнювати негативному числу.

А по-друге, якщо права частина таки позитивна (або дорівнює нулю), то можна діяти так само, як раніше: просто розкрити модуль окремо зі знаком «плюс» і окремо — зі знаком «мінус».

Таким чином, сформулюємо правило для довільних функцій $f\left(x \right)$ і $g\left(x \right)$ :

\[\left| f\left(x \right) \right|=g\left(x \right)\Rightarrow \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]

Щодо нашого рівняння отримаємо:

\[\left| 3x-2 \right|=2x\Rightarrow \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\end(align) \right.\]

Ну, з вимогою $2x\ge 0$ ми якось впораємося. Зрештою, можна тупо підставити коріння, яке ми отримаємо з першого рівняння, і перевірити: чи виконується нерівність чи ні.

Тому розв'яжемо саме рівняння:

\[\begin(align)& 3x-2=2\Rightarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Rightarrow 3x=0\Rightarrow x=0. \\end(align)\]

Ну і яке з цих двох коренів задовольняє вимогу $2x\ge 0$? Так обоє! Тому у відповідь підуть два числа: $ x = (4) / (3) \; $ і $ x = 0 $. Ось і все рішення.

Підозрюю, що хтось із учнів уже почав нудьгувати? Що ж, розглянемо ще складніше рівняння:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

Хоч воно і виглядає злісно, ​​за фактом це все те саме рівняння виду «модуль дорівнює функції»:

\[\left| f\left(x \right) \right|=g\left(x \right)\]

І вирішується воно так само:

\[\left| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Rightarrow \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x )^(3))\ge 0. \\\end(align) \right.\]

З нерівністю ми потім розберемося — воно якесь надто злісне (насправді просте, але ми його вирішувати не будемо). Поки що краще займемося отриманими рівняннями. Розглянемо перший випадок — коли модуль розкривається зі знаком «плюс»:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Ну, тут і їжу зрозуміло, що потрібно все зібрати зліва, навести подібні і подивитися, що вийде. А вийде ось що:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \&& 2((x)^(3))-3((x)^(2))=0; \\end(align)\]

Виносимо загальний множник $((x)^(2))$ за дужку і отримуємо дуже просте рівняння:

\[((x)^(2))\left(2x-3 \right)=0\Rightarrow \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(align) \right.\]

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1,5.\]

Тут ми користувалися важливою властивістю твору, заради якого ми й розкладали вихідний багаточлен на множники: твір дорівнює нулю, коли хоча б один із множників дорівнює нулю.

Тепер так само розберемося з другим рівнянням, яке виходить при розкритті модуля зі знаком «мінус»:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \&((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \&& -3((x)^(2))+2x=0; \& x\left(-3x+2 \right)=0. \\end(align)\]

Знову те саме: твір дорівнює нулю, коли дорівнює нулю хоча б один із множників. Маємо:

\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]

Ну ось ми отримали три корені: $ x = 0 $, $ x = 1,5 $ і $ x = (2) / (3) \; $. Ну, і що з цього набору піде в остаточну відповідь? Для цього пригадаємо, що ми маємо додаткове обмеження у вигляді нерівності:

Як врахувати цю вимогу? Та просто підставимо знайдене коріння і перевіримо: виконується нерівність при цих $x$ чи ні. Маємо:

\[\begin(align)& x=0\Rightarrow x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Rightarrow x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Rightarrow x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27) \ ge 0; \\end(align)\]

Таким чином, корінь $ x = 1,5 $ нас не влаштовує. І у відповідь підуть лише два корені:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

Як бачите, навіть у цьому випадку нічого складного не було – рівняння з модулями завжди вирішуються за алгоритмом. Потрібно лише добре розумітися на багаточленах і нерівностях. Тому переходимо до складніших завдань — там уже буде не один, а два модулі.

Рівняння з двома модулями

Досі ми вивчали лише найпростіші рівняння — там був один модуль і ще щось. Це "щось ще" ми відправляли в іншу частину нерівності, подалі від модуля, щоб у результаті все звелося до рівняння виду $ \ left | f\left(x \right) \right|=g\left(x \right)$ або навіть більш простому $\left| f\left(x \right) \right|=a$.

Але дитячий садок закінчився — настав час розглянути щось серйозніше. Почнемо з рівнянь такого типу:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\]

Це рівняння виду "модуль дорівнює модулю". Принципово важливим моментом є відсутність інших доданків та множників: тільки один модуль ліворуч, ще один модуль праворуч – і нічого більше.

Хтось зараз подумає, що такі рівняння вирішуються складніше, ніж те, що ми досі вивчали. А ось і ні: ці рівняння вирішуються навіть простіше. Ось формула:

\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]

Всі! Ми просто прирівнюємо підмодульні вирази, ставлячи перед одним із них знак «плюс-мінус». А потім вирішуємо отримані два рівняння - і коріння готове! Жодних додаткових обмежень, жодних нерівностей тощо. Все дуже просто.

Давайте спробуємо вирішувати таке завдання:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\]

Елементарно, Ватсон! Розкриваємо модулі:

\[\left| 2x+3 \right|=\left| 2x-7 \right|\Rightarrow 2x+3=\pm \left(2x-7 \right)\]

Розглянемо окремо кожен випадок:

\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Rightarrow 2x+3=-2x+7. \\end(align)\]

У першому рівнянні коріння немає. Тому що коли це $3=-7$? За яких значень $x$? «Який ще нафіг $x$? Ти обкурився? Там взагалі немає $x$» - скажете ви. І будете праві. Ми здобули рівність, яка не залежить від змінної $x$, і при цьому сама рівність — неправильна. Тому і немає коріння.

З другим рівнянням все трохи цікавіше, але теж дуже просто:

Як бачимо, все вирішилося буквально в пару рядків - іншого від лінійного рівняння ми й не очікували.

У результаті остаточна відповідь: $ x = 1 $.

Ну як? Важко? Звичайно, ні. Спробуємо щось ще:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\]

Знову у нас рівняння виду $ \ left | f\left(x \right) \right|=\left| g\left(x \right) \right|$. Тому одразу переписуємо його, розкриваючи знак модуля:

\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]

Можливо, хтось зараз запитає: «Гей, що за маячня? Чому «плюс-мінус» стоїть у правого вираження, а не у лівого? Спокійно зараз все поясню. Дійсно, по-хорошому ми повинні були переписати наше рівняння так:

Потім потрібно розкрити дужки, перенести всі складові в один бік від знака рівності (оскільки рівняння, очевидно, в обох випадках буде квадратним), та й далі відшукати коріння. Але погодьтеся: коли «плюс-мінус» стоїть перед трьома доданками (особливо коли один із цих доданків — квадратний вираз), це якось складніше виглядає, ніж ситуація, коли «плюс-мінус» стоїть лише перед двома доданками.

Але ж ніщо не заважає нам переписати вихідне рівняння так:

\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\Rightarrow \left| ((x)^(2))-3x+2 \right|=\left| x-1 \right|\]

Що сталося? Та нічого особливого: просто поміняли ліву та праву частину місцями. Дрібниця, яка в результаті трохи спростить нам життя.

Загалом вирішуємо це рівняння, розглядаючи варіанти з плюсом і з мінусом:

\[\begin(align)& ((x)^(2))-3x+2=x-1\Rightarrow ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Rightarrow ((x)^(2))-2x+1=0. \\end(align)\]

Перше рівняння має коріння $x=3$ та $x=1$. Друге взагалі є точним квадратом:

\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]

Тому має єдиний корінь: $x=1$. Але це коріння ми вже отримували раніше. Таким чином, у підсумкову відповідь підуть лише два числа:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

Місія виконана! Можна взяти з полиці та з'їсти пиріжок. Там їх 2, ваш середній.:)

Важливе зауваження. Наявність однакового коріння при різних варіантах розкриття модуля означає, що вихідні багаточлени розкладаються на множники, і серед цих множників обов'язково буде загальний. Дійсно:

\[\begin(align)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|; \\& \left| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\end(align)\]

Одна з властивостей модуля: $ \ left | acdot b \right|=\left| a \right|\cdot \left| b \right|$ (тобто модуль твору дорівнює добутку модулів), тому вихідне рівняння можна переписати так:

\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]

Як бачимо, у нас справді виник спільний множник. Тепер, якщо зібрати всі модулі з одного боку, можна винести цей множник за дужку:

\[\begin(align)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|; \\& \left| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\& \left| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\end(align)\]

Ну а тепер згадуємо, що добуток дорівнює нулю, коли хоча б один із множників дорівнює нулю:

\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end(align) \right.\]

Таким чином, вихідне рівняння з двома модулями звелося до двох найпростіших рівнянь, про які ми говорили на початку уроку. Такі рівняння вирішуються буквально в пару рядків.

Дане зауваження, можливо, здасться надмірно складним та незастосовним на практиці. Однак насправді вам можуть зустрітися куди складніші завдання, ніж ті, що ми сьогодні розуміємо. У них модулі можуть комбінуватися з багаточленами, арифметичним корінням, логарифмами і т.д. І в таких ситуаціях можливість знизити загальний ступінь рівняння шляхом винесення чогось за дужку може виявитися дуже доречним.

Тепер хотілося б розібрати ще одне рівняння, яке на перший погляд може здатися маревним. На ньому «залипають» багато учнів, навіть ті, які вважають, що добре розібралися в модулях.

Проте це рівняння вирішується навіть простіше, ніж те, що ми розглядали раніше. І якщо ви зрозумієте чомусь, то отримаєте ще один прийом для швидкого вирішення рівнянь з модулями.

Отже, рівняння:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]

Ні, це не друкарська помилка: між модулями саме плюс. І нам потрібно знайти, за яких $x$ сума двох модулів дорівнює нулю.:)

У чому взагалі проблема? А проблема в тому, що кожен модуль — позитивне число, або в крайньому випадку нуль. А що буде, якщо скласти два позитивні числа? Очевидно, знову позитивне число:

\[\begin(align)& 5+7=12 \gt 0; 0,004+0,0001=0,0041 0; \\& 5+0=5 \gt 0. \\\end(align)\]

Останній рядок може наштовхнути на думку: єдиний випадок, коли сума модулів дорівнює нулю - це якщо кожен модуль дорівнюватиме нулю:

\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\Rightarrow \left\( \begin(align)& \left| x-((x)^(3)) \right|=0, \\& \left|((x)^(2))+x-2 \right|=0.\\\end(align) \right.\]

А коли модуль дорівнює нулю? Тільки в одному випадку - коли підмодульний вираз дорівнює нулю:

\[((x)^(2))+x-2=0\Rightarrow \left(x+2 \right)\left(x-1 \right)=0\Rightarrow \left[ \begin(align)& x=-2 \\& x=1 \\end(align) \right.\]

Таким чином, у нас є три точки, в яких обнулюється перший модуль: 0, 1 та −1; а також дві точки, в яких обнулюється другий модуль: −2 і 1. Однак нам потрібно, щоб обидва модулі обнулялися одночасно, тому серед знайдених чисел потрібно вибрати ті, що входять до обох наборів. Очевидно, таке число лише одне: $x=1$ — це буде остаточною відповіддю.

Метод розщеплення

Що ж, ми вже розглянули купу завдань та вивчили безліч прийомів. Думаєте, на цьому все? А ось і ні! Зараз ми розглянемо заключний прийом – і водночас найважливіший. Йтиметься про розщеплення рівнянь із модулем. Про що взагалі йтиметься? Повернемося трохи назад і розглянемо якесь просте рівняння. Наприклад, це:

\[\left| 3x-5 \right|=5-3x\]

В принципі ми вже знаємо, як вирішувати таке рівняння, тому що це стандартна конструкція виду $\left| f\left(x \right) \right|=g\left(x \right)$. Але спробуємо подивитись на це рівняння трохи під іншим кутом. Точніше, розглянемо вираз, що стоїть під знаком модуля. Нагадаю, що модуль будь-якого числа може дорівнювати самому числу, а може бути протилежний цьому числу:

\[\left| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a, \quad a \lt 0. \\end(align) \right.\]

Власне, у цій неоднозначності і полягає вся проблема: оскільки число під модулем змінюється (воно залежить від змінної), нам неясно — воно позитивне чи негативне.

Але що якщо спочатку вимагати, щоб це число було позитивним? Наприклад, потрібно, щоб $3x-5 \gt 0$ — у цьому випадку ми гарантовано отримаємо позитивне число під знаком модуля, і цього самого модуля можна повністю позбутися:

Таким чином, наше рівняння перетвориться на лінійне, яке легко вирішується:

Щоправда, всі ці роздуми мають сенс лише за умови $3x-5\gt 0$ — ми самі запровадили цю вимогу, щоб однозначно розкрити модуль. Тому давайте підставимо знайдений $x=\frac(5)(3)$ в цю умову і перевіримо:

Виходить, що з зазначеному значенні $x$ наша вимога не виконується, т.к. вираз виявився рівним нулю, а нам потрібно, щоб воно було строго більше нуля. Журбинка.:(

Але нічого страшного! Адже є ще варіант $3x-5 0$. Більше того: є ще й випадок $3x-5=0$ — це також потрібно розглянути, інакше рішення буде неповним. Отже, розглянемо випадок $3x-5 \lt 0$:

Очевидно, що модуль розкриється зі знаком «мінус». Але тоді виникає дивна ситуація: і ліворуч, і праворуч у вихідному рівнянні стирчатиме той самий вираз:

Цікаво, за яких таких $x$ вираз $5-3x$ дорівнюватиме виразу $5-3x$? Від таких рівнянь навіть Капітан очевидність подавився б слиною, але ми знаємо: це рівняння є тотожністю, тобто. воно вірне за будь-яких значень змінної!

А це означає, що нас влаштують будь-які $x$. Водночас ми маємо обмеження:

Іншими словами, відповіддю буде не якесь окреме число, а цілий інтервал:

Нарешті залишилося розглянути ще один випадок: $3x-5=0$. Тут все просто: під модулем буде нуль, а модуль нуля теж дорівнює нулю (це прямо випливає з визначення):

Але тоді вихідне рівняння $ \ left | 3x-5 \right|=5-3x$ перепишеться так:

Це коріння ми вже отримували вище, коли розглядали випадок $3x-5 \gt 0$. Більше того, це корінь є рішенням рівняння $3x-5=0$ - це обмеження, яке ми самі ж і ввели, щоб обнулити модуль.

Таким чином, крім інтервалу нас влаштує ще й число, що лежить на самому кінці цього інтервалу:

Разом остаточна відповідь: $x\in \left(-\infty ;\frac(5)(3) \right]$ Не дуже звично бачити таку хрень у відповіді до досить простого (по суті - лінійного) рівняння з модулем Що ж, звикайте: в тому і полягає складність модуля, що відповіді в таких рівняннях можуть виявитися абсолютно непередбачуваними.

Куди важливіше інше: ми щойно розібрали універсальний алгоритм розв'язання рівняння з модуляєм! І складається цей алгоритм із наступних кроків:

1. Прирівняти кожен модуль, що є в рівнянні, до нуля. Отримаємо кілька рівнянь;
2. Вирішити всі ці рівняння і відзначити коріння на числовій прямій. В результаті пряма розіб'ється на кілька інтервалів, на кожному з яких всі модулі однозначно розкриваються;
3. Вирішити вихідне рівняння для кожного інтервалу та об'єднати отримані відповіді.

От і все! Залишається лише одне питання: куди подіти саме коріння, отримане на 1-му кроці? Припустимо, у нас вийшло два корені: $ x = 1 $ і $ x = 5 $. Вони розіб'ють числову пряму на 3 шматки:

Ну, і які тут інтервали? Зрозуміло, що їх три:

1. Найлівіший: $x \lt 1$ — сама одиниця в інтервал не входить;
2. Центральний: $1\le x \lt 5$ - ось тут одиниця в інтервал входить, проте не входить п'ятірка;
3. Найправіший: $x\ge 5$ - п'ятірка входить тільки сюди!

Я гадаю, ви вже зрозуміли закономірність. Кожен інтервал включає лівий кінець і не включає правий.

На перший погляд, такий запис може здатися незручним, нелогічним і взагалі якимось маревним. Але повірте: після невеликого тренування ви виявите, що саме такий підхід є найбільш надійним і при цьому не заважає однозначно розкривати модулі. Краще використовувати таку схему, ніж щоразу думати: віддавати лівий/правий кінець у поточний інтервал або «перекидати» його в наступний.

МБОУ ЗОШ №17 м. Іванова

« Рівняння з модулем»
Методична розробка

Складено

вчителем математики

20010

Пояснювальна записка

Розділ 1. Вступ

Розділ 2. Розв'язання рівнянь, що містять модуль

Глава 3. Приклади розв'язання різних рівнянь із модулем.

Пояснювальна записка.

Розділ 1. Вступ.

Розділ 1. Визначення абсолютної величини .

│ а якщо а > 0

│а│ = │ 0, якщо а = 0 (1)

- а, якщо а
Приклади: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Розкрити модуль виразу:

а) │х - 8│, якщо х > 12 б) │2х + 3│, якщо х ≤ -2 │х – 8│= х – 8 │ 2х + 3│= - 2х – 3

Розділ 2. Основні характеристики.

Розглянемо основні властивості абсолютної величини. Властивість №1: Протилежні числа мають рівні модулі, тобто. │а│=│- а│Покажемо вірність рівності. Запишемо визначення числа – а : │- а│= (2) Порівняємо сукупності (1) та (2). Очевидно, що визначення абсолютних величин чисел аі – азбігаються. Отже, │а│=│- а│
При розгляді наступних властивостей обмежимося їх формулюванням, оскільки їх доказ наводиться в Властивість №2: Абсолютна величина суми кінцевого числа дійсних чисел не перевищує суми абсолютних величин доданків: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Властивість №3: Абсолютна величина різниці двох дійсних чисел не перевищує суми їх абсолютних величин: │а - в│ ≤│а│+│в│ Властивість №4: Абсолютна величина добутку кінцевого числа дійсних чисел дорівнює добутку абсолютних величин множників: │а · в│=│а│·│в│ Властивість №5: Абсолютна величина частки дійсних чисел дорівнює частці їх абсолютних величин:

Розділ 3. Геометрична інтерпретація поняття модуля числа.

Розділ 4. Графік функції у = │х│

Розділ 5. Умовні позначення.

Розділ 2. Розв'язання рівнянь, що містять модуль.

Розділ 1. Рівняння виду │F(х)│= m

Розділ 2. Рівняння виду F(│х│) = m

Розділ 3. Рівняння виду │F(х)│ = G(х)

Розділ 4. Рівняння виду │F(x)│= F(x) та │F(x)│= - F(x)

Відповідь: х = 3.

Вправи: №12. Розв'яжіть рівняння, у відповіді вкажіть ціле коріння: │х 2 + 6х + 8│= х 2 + 6х + 8 №13. Розв'яжіть рівняння, у відповіді вкажіть число цілих рішень: │13х – х 2 - 36│+ х 2 – 13х + 36 = 0 №14. Розв'яжіть рівняння, у відповіді вкажіть ціле число, що не є коренем рівняння:

Розділ 5. Рівняння виду │F(x)│= │G(x)│

Розділ 6. Приклади розв'язання нестандартних рівнянь

№1. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: х · │х│- 5х – 6 = 0
Відповідь: сума коренів дорівнює 1 №2. . Розв'яжіть рівняння, у відповіді вкажіть менший корінь: х 2 - 4х ·
- 5 = 0
Відповідь: менший корінь х = – 5. №3. Розв'яжіть рівняння:

Відповідь: х = -1. Вправи: №18. Розв'яжіть рівняння та вкажіть суму коренів: х · │3х + 5│= 3х 2 + 4х + 3
№19. Розв'яжіть рівняння: х 2 – 3х =

№20. Розв'яжіть рівняння:

Розділ 7. Рівняння виду │F(x)│+│G(x)│=0

)│=0

Розділ 8. Рівняння виду │а 1 х + у 1 │±│а 2 х + у 2 │± … │а n х +в n │= m

Розділ 9. Рівняння, що містять декілька модулів

Приклади: №1. Розв'яжіть рівняння:
Відповідь: х = 1; - 11. №2. Розв'яжіть рівняння:
Відповідь: х = 0; 4; - 4. №3. Розв'яжіть рівняння, у відповіді вкажіть добуток коріння:
Відповідь: добуток коренів дорівнює - 8. №4. Розв'яжіть рівняння:
Позначимо рівняння сукупності (1) і (2) та розглянемо рішення кожного з них окремо для зручності оформлення. Так як обидва рівняння містять більше одного модуля, зручніше здійснити рівносильний перехід до сукупностей систем. (1)

(2)


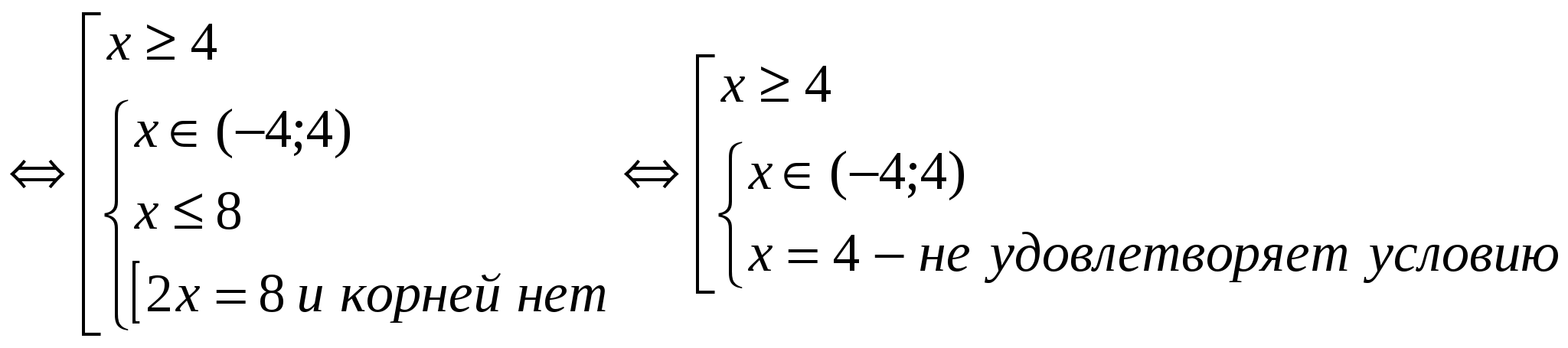Відповідь:
Вправи: №36. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: 5 │3х-5│ = 25 х №37. Розв'яжіть рівняння, якщо коріння більше одного, у відповіді вкажіть суму коренів: │х + 2│ х – 3х – 10 = 1 №38. Розв'яжіть рівняння: 3 │2х -4│ = 9 │х│ №39. Розв'яжіть рівняння, у відповіді вкажіть кількість коренів на : 2 │ sin х│ = √2 №40 . Розв'яжіть рівняння, у відповіді вкажіть кількість коренів:

Розділ 3. Логарифмічні рівняння.

1 випадок: якщо х ≥ - 1, то log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – задовольняє умові х ≥ - 1 2 випадок: якщо х log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – задовольняє умові х - 1
Відповідь: добуток коренів дорівнює - 15.
№2. Розв'яжіть рівняння, у відповіді вкажіть суму коренів: lg
О.Д.З.

Відповідь: сума коренів дорівнює 0,5.
№3. Розв'яжіть рівняння: log 5
О.Д.З.

Відповідь: х = 9. №4. Розв'яжіть рівняння: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ О.Д.З. х > 0 Скористаємося формулою переходу до іншої основи. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Знайдемо нулі підмодульних виразів: х = 25; х = Ці числа ділять область допустимих значень на три інтервали, тому рівняння рівносильне сукупності трьох систем.
Відповідь: )