Знайти невизначений інтеграл x 1. Методи обчислення невизначених інтегралів

А чи можна під знак диференціала підбивати нелінійну функцію? Так, якщо підінтегральний вираз є твір двох множників: один множник — складна функція від якоїсь нелінійної функції, а інший множник є похідною від цієї нелінійної функції. Розглянемо сказане на прикладах.

Знайти невизначені інтеграли.

Приклад 1. ∫(2x + 1)(x 2 + x + 2) 5 dx = ∫(x 2 + x + 2) 5 d (x 2 + x + 2) =(x²+x+2) 6 : 6+C.

Що являє собою цей підінтегральний вираз? Добуток статечної функції від (х 2 + х + 2) і множника (2х + 1), який дорівнює похідній від основи ступеня: (х 2 + х + 2)" = 2х + 1.

Це дозволило нам підвести (2х + 1) під знак диференціала:

∫u 5 du=u 6 : 6+ C. (Формула 1). )

Перевірка. (F(x)+C)" =((x²+x+2) 6 : 6 + C) = 1/6 · 6 (x 2 + x + 2) 5 · (x 2 + x + 2)" =

= (x 2 + x + 2) 5 · (2x + 1) = (2x + 1) (x 2 + x + 2) 5 = f (x).

приклад 2.∫(3x 2 – 2x + 3)(x 3 - x 2 + 3x + 1) 5 dx = ∫(x 3 – x 2 + 3x + 1) 5 d (x 3 – x 2 + 3x + 1) =

=(x³- x²+3x+1) 6 : 6 + C

І чим цей приклад відрізняється від прикладу 1? Та нічим! Той самий п'ятий ступінь з основою (х 3 – х 2 + 3х + 1) множиться на тричлен (3х 2 – 2х + 3), який є похідною основи ступеня: (х 3 – х 2 + 3х + 1)" = 3х 2 - 2х + 3. Це підставу ступеня ми і підвели під знак диференціала, від чого значення підінтегрального виразу не змінилося, а потім застосували ту ж формулу 1). Інтеграли)

приклад 3.

Тут похідна від (2х3 – 3х) дасть (6х2 – 3), а у нас

є (12х 2 – 6), тобто вираз у 2 рази більше, значить, підіб'ємо (2х 3 – 3х) під знак диференціала, а перед інтегралом поставимо множник 2 . Застосуємо формулу 2) (лист ).

Ось що вийде:

Зробимо перевірку, враховуючи, що:

приклади. Знайти невизначені інтеграли.

1. ∫(6х+5) 3 dx. Як вирішуватимемо? Дивимося в лист і міркуємо приблизно так: підінтегральна функція є ступенем, а у нас є формула для інтеграла ступеня (формула 1) ), але в ній підстава ступеня uта змінна інтегрування теж u.

А у нас змінна інтеграція х, а основа ступеня (6х+5). Зробимо заміну змінної інтегрування: замість dx запишемо d(6х+5). Що змінилося? Оскільки те, що стоїть після знака диференціала d, за замовчуванням, диференціюється,

то d(6x+5)=6dx, тобто. при заміні змінної х на змінну (6х+5) підінтегральна функція зросла у 6 разів, тому перед знаком інтеграла ставимо множник 1/6. Записати ці міркування можна так:

Отже, ми вирішили цей приклад запровадженням нової змінної (змінну х замінили на змінну 6х+5). А куди записали нову змінну (6х+5)? Під знак диференціалу. Тому, цей метод введення нової змінної часто називають методом (або способом ) підведення(новою змінною ) під знак диференціала.

У другому прикладі ми спочатку отримали ступінь з негативним показником, а потім підвели під знак диференціала (7х-2) і використали формулу інтеграла ступеня 1) (Інтеграли ).

Розберемо рішення прикладу 3.

Перед інтегралом стоїть коефіцієнт 1/5. Чому? Так як d (5x-2) = 5dx, то, підвівши під знак диференціала функцію u = 5x-2, ми збільшили підінтегральний вираз у 5 разів, тому щоб значення даного виразу не змінилося - треба було розділити на 5, тобто . помножити на 1/5. Далі була використана формула 2) (Інтеграли) .

Усі найпростіші формули інтегралів матимуть вигляд:

∫f(x) dx=F(x)+C, причому, повинна виконуватись рівність:

(F(x)+C)"=f(x).

Формули інтегрування можна отримати зверненням відповідних формул диференціювання.

Справді,

Показник ступеня nможе бути і дрібним. Часто доводиться знаходити невизначений інтеграл від функції у=х. Обчислимо інтеграл від функції f(x)=√x, використовуючи формулу 1) .

Запишемо цей приклад у вигляді формули 2) .

Оскільки (х+С)"=1, то ∫dx=x+C.

3) ∫dx=x+C.

Замінюючи 1/х ² на х -2, обчислимо інтеграл від 1/х ².

А можна було отримати цю відповідь зверненням відомої формули диференціювання:

Запишемо наші міркування у вигляді формули 4).

Помноживши обидві частини набутої рівності на 2, отримаємо формулу 5).

Знайдемо інтеграли від основних тригонометричних функцій, знаючи їх похідні: (sinx) = cosx; (cosx) = sinx; (tgx)"=1/cos²x; (ctgx)"=-1/sin²x. Отримуємо формули інтегрування 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

Після вивчення показової та логарифмічної функцій, додамо ще кілька формул.

Основні характеристики невизначеного інтеграла.

I.Похідна невизначеного інтеграла дорівнює підінтегральній функції .

(∫f(x) dx)"=f(x).

ІІ.Диференціал невизначеного інтеграла дорівнює підінтегральному виразу.

d∫f(x) dx=f(x) dx.

ІІІ.Невизначений інтеграл від диференціала (похідної) деякої функції дорівнює сумі цієї функції та довільної постійної З.

∫dF(x)=F(x)+Cабо ∫F"(x) dx=F(x)+C.

Зверніть увагу: у I, II та III властивостях знаки диференціала та інтеграла (інтеграла та диференціала) «з'їдають» один одного!

IV.Постійний множник підінтегрального виразу можна винести знак інтеграла.

∫kf (x) dx=k·∫f (x) dx,де k- Постійна величина, що не дорівнює нулю.

V.Інтеграл від алгебраїчної суми функцій дорівнює сумі алгебри інтегралів від цих функцій.

∫(f(x)±g(x)) dx=∫f(x) dx±∫g(x) dx.

VI.Якщо F(x) є первісною для f(x), а kі b- Постійні величини, причому, k≠0, то (1/k)·F (kx+b) є первісною для f (kx+b). Справді, за правилом обчислення похідної складної функції маємо:

Можна записати:

Для кожної математичної дії існує протилежна йому дія. Для дії диференціювання (знаходження похідних функцій) також існує зворотна дія - інтегрування. За допомогою інтегрування знаходять (відновлюють) функцію за заданою похідною або диференціалу. Знайдену функцію називають первісної.

Визначення.Диференційована функція F(x)називається первісною для функції f(x)на заданому проміжку, якщо для всіх хз цього проміжку справедлива рівність: F′(x)=f(x).

приклади. Знайти первісні для функцій: 1) f(x) = 2x; 2) f(x) = 3cos3x.

1) Оскільки (х²)′=2х, то, за визначенням, функція F(x)=x² буде першорядною для функції f(x)=2x.

2) (sin3x)′=3cos3x. Якщо позначити f(x)=3cos3x і F(x)=sin3x, то, за визначенням первісної, маємо: F′(x)=f(x), і, отже, F(x)=sin3x є первісною для f( x) = 3cos3x.

Зауважимо, що і (sin3x +5 )′= 3cos3xі (sin3x -8,2 )′= 3cos3x, ... у загальному вигляді можна записати: (sin3x +С)′= 3cos3x, де З- Деяка постійна величина. Ці приклади говорять про неоднозначність дії інтегрування, на відміну від дії диференціювання, коли в будь-якій функції, що диференціюється, існує єдина похідна.

Визначення.Якщо функція F(x)є первісною для функції f(x)на деякому проміжку, то безліч всіх первісних цієї функції має вигляд:

F(x)+Cде С - будь-яке дійсне число.

Сукупність всіх первісних F (x) + C функції f (x) на проміжку, що розглядається, називається невизначеним інтегралом і позначається символом ∫ (Знак інтеграла). Записують: ∫f(x) dx=F(x)+C.

Вираз ∫f (x) dxчитають: «інтеграл еф від ікс до де ікс».

f(x) dx- Підінтегральний вираз,

f(x)- Підінтегральна функція,

х- Змінна інтегрування.

F(x)- Первісна для функції f(x),

З- Деяка постійна величина.

Тепер розглянуті приклади можна записати так:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Що означає знак d?

d -знак диференціала - має подвійне призначення: по-перше, цей знак відокремлює підінтегральну функцію від змінної інтегрування; по-друге, все, що стоїть після цього знака, диференціюється за умовчанням і множиться на підінтегральну функцію.

приклади. Знайти інтеграли: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Після піктограми диференціалу dстоїть хх, а р

∫ 2хрdx=рх²+С. Порівняйте з прикладом 1).

Зробимо перевірку. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) Після піктограми диференціалу dстоїть р. Отже, змінна інтеграція р, а множник хслід вважати деякою постійною величиною.

∫ 2хрdр=р²х+С. Порівняйте з прикладами 1) і 3).

Зробимо перевірку. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Сторінка 1 з 1 1

Знайти невизначений інтеграл (безліч первісних або "антипохідних") означає відновити функцію за відомою похідною цієї функції. Відновлена ​​безліч первісних F(x) + З для функції f(x) враховує константу інтегрування C. За швидкістю переміщення матеріальної точки (похідної) то, можливо відновлено закон руху цієї точки (первообразная); щодо прискорення руху точки - її швидкість та закон руху. Як бачимо, інтегрування - широке полі діяльності Шерлоков Холмсов від фізики. Та й в економіці багато понять надаються через функції та їх похідні і тому, наприклад, можна за продуктивністю праці у певний момент часу (похідної) відновити обсяг продукції, випущений у відповідний час.

Щоб знайти невизначений інтеграл, потрібна досить невелика кількість основних формул інтегрування. Але процес його знаходження значно важче, ніж лише застосування цих формул. Вся складність відноситься не до інтегрування, а до приведення інтегрованого виразу до такого виду, що дає можливість знайти невизначений інтеграл за вищезазначеними основними формулами. Це означає, що для початку практики інтегрування потрібно активізувати набуті в середній школі навички перетворення виразів.

Вчитися знаходити інтеграли будемо, користуючись властивостями та таблицею невизначених інтегралівз уроку про основні поняття цієї теми (відкриється у новому вікні).

Існує кілька методів знаходження інтеграла, з яких метод заміни змінноїі метод інтегрування частинами- обов'язковий джентльменський набір кожного, хто успішно здав найвищу математику. Однак починати освоювати інтегрування корисніше і приємніше із застосуванням методу розкладання, заснованому на двох теоремах про властивості невизначеного інтеграла, які для зручності повторимо тут.

Теорема 3.Постійний множник у подинтегральном вираженні можна виносити за знак невизначеного інтеграла, тобто.

Теорема 4.Невизначений інтеграл суми алгебри кінцевого числа функцій дорівнює сумі алгебри невизначених інтегралів цих функцій, тобто.

(2)

Крім того, в інтегруванні може стати в нагоді наступне правило: якщо вираз підінтегральної функції містить постійний множник, то вираз первісної домножується на число, зворотне постійному множнику, тобто

(3)

Оскільки цей урок - вступний у вирішення завдань інтегрування, важливо відзначити дві речі, які або вже на початковому етапі, або трохи пізніше можуть вас здивувати. Здивування пов'язане з тим фактом, що інтегрування - операція, зворотна диференціюванню і невизначений інтеграл можна справедливо називати "антипохідною".

Перша річ, якою не слід дивуватися при інтегруванні.У таблиці інтегралів існують формули, які не мають аналогів серед формул похідної таблиці . Це такі формули:

Однак можна переконатися в тому, що похідні виразів, що стоять у правих частинах цих формул, збігаються з відповідними підінтегральними функціями.

Друга річ, якій не слід дивуватися при інтегруванні. Хоча похідна будь-якої елементарної функції є також елементарною функцією, невизначені інтеграли від деяких елементарних функцій вже не є елементарними функціями . Прикладами таких інтегралів можуть бути такі:

Для вироблення техніки інтегрування стануть у нагоді такі навички: скорочення дробів, розподіл багаточлена в чисельнику дробу на одночлен у знаменнику (для отримання суми невизначених інтегралів), перетворення коренів у ступені, множення одночлена на багаточлен, зведення в ступінь. Ці навички потрібні для перетворень підінтегрального виразу, у яких має вийти сума інтегралів, присутніх у таблиці інтегралів.

Знаходимо невизначені інтеграли разом

приклад 1.Знайти невизначений інтеграл

.

Рішення. Бачимо у знаменнику підінтегрального виразу багаточлен, у якому ікс у квадраті. Це майже вірна ознака того, що можна застосувати табличний інтеграл 21 (з арктангенсом у результаті). Виносимо із знаменника множник-двійку (є така властивість інтеграла - постійний множник можна виносити за знак інтеграла, вище воно було згадано як теорема 3). Результат всього цього:

Тепер у знаменнику є сума квадратів, а це означає, що можемо застосувати згаданий табличний інтеграл. Остаточно отримуємо відповідь:

.

приклад 2.Знайти невизначений інтеграл

Рішення. Знову застосовуємо теорему 3 - властивість інтеграла, на підставі якого постійний множник можна виносити за знак інтеграла:

Застосовуємо формулу 7 з таблиці інтегралів (змінна до ступеня) до підінтегральної функції:

.

Скорочуємо дроби і перед нами кінцева відповідь:

приклад 3.Знайти невизначений інтеграл

Рішення. Застосовуючи спочатку теорему 4, а потім теорему 3 про властивості знайдемо даний інтеграл як суму трьох інтегралів:

Усі три отримані інтеграли – табличні. Використовуємо формулу (7) з таблиці інтегралів при n = 1/2, n= 2 і n= 1/5, і тоді

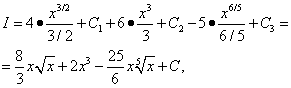
поєднує всі три довільні постійні, які були запроваджені при знаходженні трьох інтегралів. Тому в аналогічних ситуаціях слід запроваджувати лише одну довільну постійну (константу) інтегрування.

приклад 4.Знайти невизначений інтеграл

Рішення. Коли знаменнику подинтегральной дробу - одночлен, можемо почленно розділити чисельник на знаменник. Вихідний інтеграл перетворився на суму двох інтегралів:

.

Щоб застосувати табличний інтеграл, перетворимо коріння в міру і ось вже остаточна відповідь:

Продовжуємо знаходити невизначені інтеграли разом

Приклад 7.Знайти невизначений інтеграл

Рішення. Якщо ми перетворимо підінтегральну функцію, звівши двочлен у квадрат і розділивши почленно чисельник на знаменник, то вихідний інтеграл стане сумою трьох інтегралів.

Знаходження невизначеного інтеграла дуже частою завданням у вищої математики та інших технічних розділах науки. Навіть рішення найпростіших фізичних завдань не обходиться без обчислення кількох простих інтегралів. Тому зі шкільного віку нас навчають прийомів та методів вирішення інтегралів, наводяться численні таблиці з інтегралами найпростіших функцій. Однак з часом все це благополучно забувається, або у нас не вистачає часу на розрахунки, або нам потрібно знайти рішення невизначеного інтегралудуже складної функції. Для вирішення цих проблем вам буде незамінний наш сервіс, що дозволяє безпомилково знаходити невизначений інтеграл онлайн.

Вирішити невизначений інтеграл

Онлайн сервіс на сайтдозволяє знаходити рішення інтеграла онлайншвидко, безкоштовно та якісно. Ви можете замінити пошук за таблицями потрібного інтеграла нашим сервісом, де швидко ввівши потрібну функцію, ви отримаєте рішення невизначеного інтеграла в табличному варіанті. Не всі математичні сайти здатні обчислювати невизначені інтеграли функцій в режимі онлайн швидко та якісно, ​​особливо якщо потрібно знайти невизначений інтегралвід складної функції або таких функцій, які не включені до загального курсу вищої математики. Сайт сайтдопоможе вирішити інтеграл онлайн і впоратися із поставленим завданням. Використовуючи онлайн рішення інтеграла на сайті сайт, ви завжди отримаєте точну відповідь.

Навіть якщо ви хочете обчислити інтеграл самостійно, завдяки нашому сервісу вам буде легко перевірити свою відповідь, знайти допущену помилку чи описку, або переконатися в бездоганному виконанні завдання. Якщо ви вирішуєте завдання і вам, як допоміжну дію, необхідно обчислити невизначений інтеграл, то навіщо витрачати час на ці дії, які, можливо, ви вже виконували тисячу разів? Тим більше, що додаткові розрахунки інтеграла можуть бути причиною описки або маленької помилки, які згодом призвели до невірної відповіді. Просто скористайтесь нашими послугами та знайдіть невизначений інтеграл онлайнбез будь-яких зусиль. Для практичних завдань знаходження інтегралафункції онлайнцей сервер дуже корисний. Необхідно ввести задану функцію, отримати онлайн рішення невизначеного інтегралута порівняти відповідь з вашим рішенням.

Наведено огляд методів обчислення невизначених інтегралів. Розглянуто основні методи інтегрування, які включають інтегрування суми і різниці, винесення постійної за знак інтеграла, заміну змінної, інтегрування частинами. Також розглянуто спеціальні методи та прийоми інтегрування дробів, коренів, тригонометричних та показових функцій.

Первісна і невизначений інтеграл

Первісна F(x) від функції f(x) - це така функція, похідна якої дорівнює f(x) :
F′(x) = f(x), x ∈ Δ,
де Δ - Проміжок, на якому виконується дане рівняння.

Сукупність всіх первісних називається невизначеним інтегралом:
,
де C - постійна, яка залежить від змінної x .

Основні формули та методи інтегрування

Таблиця інтегралів

Кінцева мета обчислення невизначених інтегралів – шляхом перетворень, привести заданий інтеграл до виразу, що містить найпростіші чи табличні інтеграли.
Див. Таблиця інтегралів >>>

Правило інтегрування суми (різниці)

Винесення постійної за знак інтегралу

Нехай c - постійна, що не залежить від x. Тоді її можна винести за знак інтегралу:

Заміна змінної

Нехай x - функція від змінної t x = φ(t) тоді
.
Або навпаки, t = φ(x) ,
.

За допомогою заміни змінної можна обчислити прості інтеграли, а й спростити обчислення складніших.

Правило інтегрування частинами

Інтегрування дробів (раціональних функцій)

Введемо позначення. Нехай P k (x), Q m (x), R n (x) позначають багаточлени ступенів k, m, n відповідно щодо змінної x .

Розглянемо інтеграл, що складається з дробу багаточленів (так звана раціональна функція):

Якщо k ≥ n, то спочатку потрібно виділити цілу частину дробу:
.
Інтеграл від многочлена S k-n(x) обчислюється за таблицею інтегралів.

Залишається інтеграл:
де m< n .
Для його обчислення, підінтегральний вираз слід розкласти на найпростіші дроби.

Для цього потрібно знайти коріння рівняння:
Q n (x) = 0.
Використовуючи отримане коріння, потрібно уявити знаменник у вигляді твору співмножників:
Q n (x) = s (x-a) n a (x-b) n b ... (x 2 +ex+f) n e (x 2 +gx+k) n g ....
Тут s-коефіцієнт при x n, x 2 + ex + f > 0, x 2 + gx + k > 0, ....

Після цього розкласти дріб на найпростіші:

Інтегруючи, отримуємо вираз, що складається з найпростіших інтегралів.
Інтеграли виду

приводяться до табличних підстановкою t = x - a.

Розглянемо інтеграл:

Перетворимо чисельник:
.
Підставляючи в підінтегральний вираз, отримуємо вираз, до якого входять два інтеграли:
,
.
Перший, підстановкою t = x 2 + ex + f наводиться до табличного.
Другий, за формулою приведення:

наводиться до інтегралу

Наведемо його знаменник до суми квадратів:
.
Тоді підстановкою, інтеграл

також наводиться до табличного.

Інтегрування ірраціональних функцій

Введемо позначення. Нехай R(u 1 , u 2 , ... , u n ) означає раціональну функцію від змінних u 1 , u 2 , ... , u n . Тобто
,
де P, Q - многочлен від змінних u 1 , u 2 , ... , u n .

Дробно-лінійна ірраціональність

Розглянемо інтеграли виду:
,
де - раціональні числа, m 1 , n 1 , ..., m s , ns - цілі числа.
Нехай n - загальний знаменник чисел r1, ..., rs.
Тоді інтеграл зводиться до інтегралу від раціональних функцій підстановкою:
.

Інтеграли від диференціальних біномів

Розглянемо інтеграл:
,
де m, n, p – раціональні числа, a, b – дійсні числа.
Такі інтеграли зводяться до інтегралів від раціональних функцій у трьох випадках.

1) Якщо p – ціле. Підстановка x = t N де N - загальний знаменник дробів m і n .
2) Якщо – ціле. Підстановка a x n + b = t M де M - знаменник числа p .
3) Якщо – ціле. Підстановка a + b x - n = t M де M - знаменник числа p .

Якщо жодне з трьох чисел не є цілим числом, то за теоремою Чебишева інтеграли цього виду не можуть бути виражені кінцевою комбінацією елементарних функцій.

У ряді випадків, спочатку буває корисним привести інтеграл до зручніших значень m і p. Це можна зробити за допомогою формул приведення:
;
.

Інтеграли, що містять квадратний корінь із квадратного тричлена

Тут ми розглядаємо інтеграли виду:
,

Підстановки Ейлера

Такі інтеграли можуть бути зведені до інтегралів від раціональних функцій однієї з трьох підстановок Ейлера:
, при a > 0;
при c > 0 ;
де x 1 - корінь рівняння a x 2 + b x + c = 0. Якщо це рівняння має дійсне коріння.

Тригонометричні та гіперболічні підстановки

Прямі методи

Найчастіше, підстановки Ейлера призводять до довшим обчислень, ніж прямі методи. За допомогою прямих методів інтеграл наводиться до одного з наведених нижче видів.

І тип

Інтеграл виду:
,
де P n (x) - багаточлен ступеня n .

Такі інтеграли є методом невизначених коефіцієнтів, використовуючи тотожність:

Диференціюючи це рівняння та прирівнюючи ліву та праву частини, знаходимо коефіцієнти A i .

II тип

Інтеграл виду:
,
де P m (x) - багаточлен ступеня m.

Підстановкою t = (x - α) -1цей інтеграл наводиться до попереднього типу. Якщо m ≥ n, то у дробу слід виділити цілу частину.

III тип

Третій і найскладніший тип:
.

Тут потрібно зробити підстановку:
.
Після чого інтеграл набуде вигляду:
.
Далі постійні α, β потрібно вибрати такими, щоб коефіцієнти при t звернулися в нуль:
B = 0, B 1 = 0.
Тоді інтеграл розпадається на суму інтегралів двох видів:
;
,
які інтегруються, відповідно до підстановок:
z 2 = A 1 t 2 + C 1;
y 2 = A 1 + C 1 t -2.

Загальний випадок

Інтегрування трансцендентних (тригонометричних та показових) функцій

Заздалегідь зазначимо, що ті методи, які застосовуються для тригонометричних функцій, також застосовуються і для гіперболічних функцій. З цієї причини ми не розглядатимемо інтегрування гіперболічних функцій окремо.

Інтегрування раціональних тригонометричних функцій від cos x та sin x

Розглянемо інтеграли від тригонометричних функцій виду:
,
де R – раціональна функція. Сюди також можуть входити тангенси та котангенси, які слід перетворити через синуси та косинуси.

При інтегруванні таких функцій корисно мати на увазі три правила:
1) якщо R( cos x, sin x)множиться на -1 від зміни знака перед однією з величин cos xабо sin x, то корисно іншу з них позначити через t.
2) якщо R( cos x, sin x)не змінюється від зміни знака одночасно перед cos xі sin x, то корисно покласти tg x = tабо ctg x = t.
3) підстановка у всіх випадках призводить до інтегралу від раціонального дробу. На жаль, ця підстановка призводить до більш довгих обчислень, ніж попередні, якщо вони застосовні.

Добуток статечних функцій від cos x і sin x

Розглянемо інтеграли виду:

Якщо m і n – раціональні числа, то однією з підстановок t = sin xабо t = cos xінтеграл зводиться до інтегралу диференціального бінома.

Якщо m і n - цілі числа, то інтеграли обчислюються інтегруванням частинами. При цьому виходять такі формули:

;
;
;
.

Інтегрування частинами

Застосування формули Ейлера

Якщо підінтегральний вираз лінійний щодо однієї з функцій
cos axабо sin ax, то зручно застосувати формулу Ейлера:
e iax = cos ax + isin ax(Де i 2 = - 1 ),
замінивши цю функцію на e iaxта виділивши дійсну (при заміні cos ax) або уявну частину (при заміні sin ax) з отриманого результату.

Використана література:
Н.М. Гюнтер, Р.О. Кузьмін, Збірник завдань з вищої математики, "Лань", 2003.

Рішення інтегралів – завдання легке, але тільки для обраних. Ця стаття для тих, хто хоче навчитися розуміти інтеграли, але не знає про них нічого чи майже нічого. Інтеграл... Навіщо він потрібний? Як його обчислювати? Що таке певний та невизначений інтеграли? Якщо єдине відоме вам застосування інтеграла – діставати гачком у формі значка інтеграла щось корисне з важкодоступних місць, тоді ласкаво просимо! Дізнайтеся, як вирішувати інтеграли і чому без цього не можна обійтися.

Вивчаємо поняття "інтеграл"

Інтегрування було відоме ще у Стародавньому Єгипті. Звичайно, не в сучасному вигляді, але все ж таки. З того часу математики написали дуже багато книг на цю тему. Особливо відзначилися Ньютон і Лейбніц але суть речей не змінилася. Як зрозуміти інтеграли з нуля? Ніяк! Для розуміння цієї теми все одно знадобляться базові знання основ математичного аналізу. Саме ці фундаментальні відомості про Ви знайдете у нас у блозі.

Невизначений інтеграл

Нехай у нас є якась функція f(x) .

Невизначеним інтегралом функції f(x) називається така функція F(x) , похідна якої дорівнює функції f(x) .

Тобто інтеграл - це похідна навпаки або первинна. До речі, про те, як читайте у нашій статті.

Первісна існує для всіх безперервних функцій. Також до первісної часто додають символ константи, оскільки похідні функцій, що різняться на константу, збігаються. Процес знаходження інтеграла називається інтегруванням.

Простий приклад:

Щоб постійно не вираховувати первісні елементарні функції, їх зручно звести в таблицю і користуватися вже готовими значеннями:

Визначений інтеграл

Маючи справу з поняттям інтеграла, ми маємо справу з нескінченно малими величинами. Інтеграл допоможе обчислити площу фігури, масу неоднорідного тіла, пройдений при нерівномірному русі шлях та багато іншого. Слід пам'ятати, що інтеграл - це сума нескінченно великої кількості нескінченно малих доданків.

Як приклад уявімо графік якоїсь функції. Як знайти площу фігури, обмеженої графіком функції?

За допомогою інтегралу! Розіб'ємо криволінійну трапецію, обмежену осями координат і графіком функції, на нескінченно малі відрізки. Таким чином фігура виявиться розділена на тонкі стовпчики. Сума площ стовпчиків і становитиме площу трапеції. Але пам'ятайте, що таке обчислення дасть зразковий результат. Однак що менше і вже будуть відрізки, то точніше буде обчислення. Якщо ми зменшимо їх настільки, що довжина буде прагнути до нуля, то сума площ відрізків буде прагнути до площі фігури. Це і є певний інтеграл, який записується так:

Точки а та b називаються межами інтегрування.

Барі Алібасов та гурт "Інтеграл"

До речі! Для наших читачів зараз діє знижка 10% на

Правила обчислення інтегралів для чайників

Властивості невизначеного інтегралу

Як вирішувати невизначений інтеграл? Тут ми розглянемо властивості невизначеного інтеграла, які стануть у нагоді при вирішенні прикладів.

• Похідна від інтеграла дорівнює підінтегральній функції:

• Константу можна виносити з-під знаку інтеграла:

• Інтеграл від суми дорівнює сумі інтегралів. Правильно також для різниці:

Властивості певного інтегралу

• Лінійність:

• Знак інтеграла змінюється, якщо поміняти місцями межі інтегрування:

• При будь-якихточках a, bі з:

Ми вже з'ясували, що певний інтеграл – це межа суми. Але як отримати конкретне значення під час вирішення прикладу? Для цього існує формула Ньютона-Лейбніца:

Приклади вирішення інтегралів

Нижче розглянемо кілька прикладів знаходження невизначених інтегралів. Пропонуємо Вам самостійно розібратися у тонкощах рішення, а якщо щось незрозуміло, ставте запитання у коментарях.

Для закріплення матеріалу перегляньте відео про те, як вирішуються інтеграли на практиці. Не впадаєте у відчай, якщо інтеграл не дається відразу. Запитайте, і вони розкажуть вам про обчислення інтегралів все, що знають самі. З нашою допомогою будь-який потрійний або криволінійний інтеграл замкнутої поверхні стане вам під силу.