Зворотна матриця 2 на формулу 2. Повторення: множення матриць
Матриця А -1 називається зворотною матрицею по відношенню до матриці А, якщо А * А -1 = Е де Е - одинична матриця n -го порядку. Зворотна матриця може існувати лише для квадратних матриць.
Призначення сервісу. За допомогою даного сервісу в онлайн режимі можна знайти додатки алгебри , транспоновану матрицю A T , союзну матрицю і зворотну матрицю. Рішення проводиться безпосередньо на сайті (в онлайн) і є безкоштовним. Результати обчислень оформляються у звіті формату Word та у форматі Excel (тобто є можливість перевірити рішення). див. приклад оформлення.
Інструкція. Для отримання рішення необхідно встановити розмірність матриці. Далі в новому діалоговому вікні заповніть матрицю A.
також Зворотня матриця методом Жордано-Гаусса
Алгоритм знаходження зворотної матриці
- Знаходження транспонованої матриці A T .
- Визначення додатків алгебри. Замінюють кожен елемент матриці його додатком алгебри.
- Складання зворотної матриці з додатків алгебри: кожен елемент отриманої матриці ділять на визначник вихідної матриці. Результуюча матриця є зворотною для вихідної матриці.
- Визначають, чи квадратна матриця. Якщо ні, то зворотної матриці не існує.
- Обчислення визначника матриці A. Якщо він не дорівнює нулю, продовжуємо рішення, інакше – зворотної матриці не існує.
- Визначення додатків алгебри.
- Заповнення союзної (взаємної, приєднаної) матриці C .
- Складання зворотної матриці з додатків алгебри: кожен елемент приєднаної матриці C ділять на визначник вихідної матриці. Результуюча матриця є зворотною для вихідної матриці.
- Роблять перевірку: перемножують вихідну та отриману матриці. В результаті повинна вийти поодинока матриця.
Приклад №1. Запишемо матрицю у вигляді:
Алгебраїчні доповнення.
| A 1,1 = (-1) 1+1 |
|
∆ 1,1 = (-1 4-5 (-2)) = 6
| A 1,2 = (-1) 1+2 |
|
∆ 1,2 = -(2 4-(-2 (-2))) = -4
| A 1,3 = (-1) 1+3 |
|
∆ 1,3 = (2 5-(-2 (-1))) = 8
| A 2,1 = (-1) 2+1 |
|
∆ 2,1 = -(2 4-5 3) = 7
| A 2,2 = (-1) 2+2 |
|
∆ 2,2 = (-1 4-(-2 3)) = 2
| A 2,3 = (-1) 2+3 |
|
∆ 2,3 = -(-1 5-(-2 2)) = 1
| A 3,1 = (-1) 3+1 |
|
∆ 3,1 = (2 (-2)-(-1 3)) = -1
| A 3,2 = (-1) 3+2 |
|
∆ 3,2 = -(-1 (-2)-2 3) = 4
| A 3,3 = (-1) 3+3 |
|
∆ 3,3 = (-1 (-1)-2 2) = -3
Тоді зворотну матрицюможна записати як:
| A -1 = 1/10 |
|
| A -1 = |
|
Інший алгоритм знаходження зворотної матриці
Наведемо іншу схему знаходження зворотної матриці.- Знаходимо визначник цієї квадратної матриці A .
- Знаходимо додатки алгебри до всіх елементів матриці A .
- Записуємо додатки алгебри елементів рядків в стовпці (транспонування).
- Ділимо кожен елемент отриманої матриці на визначник матриці A.
Особливий випадок: Зворотній, по відношенню до одиничної матриці E є одинична матриця E .
Матриця $A^(-1)$ називається зворотної по відношенню до квадратної матриці $A$, якщо виконано умову $A^(-1)\cdot A=A\cdot A^(-1)=E$, де $E $ - Поодинока матриця, порядок якої дорівнює порядку матриці $ A $.
Невироджена матриця - матриця, визначник якої не дорівнює нулю. Відповідно, вироджена матриця - та, у якої дорівнює нулю визначник.
Зворотна матриця $A^(-1)$ існує і тоді, коли матриця $A$ – невироджена. Якщо зворотна матриця $A^(-1)$ існує, вона єдина.
Є кілька способів знаходження зворотної матриці, і ми розглянемо два їх. На цій сторінці буде розглянуто метод приєднаної матриці, який належить стандартним у більшості курсів вищої математики. Другий спосіб знаходження зворотної матриці (метод елементарних перетворень), який передбачає використання методу Гаусса або Гаусса-Жордана, розглянутий у другій частині .
Метод приєднаної (союзної) матриці
Нехай задано матрицю $A_(n\times n)$. Для того щоб знайти зворотну матрицю $A^(-1)$, потрібно здійснити три кроки:
- Знайти визначник матриці $A$ і переконатися, що $Delta Aneq 0$, тобто. що матриця А – невироджена.
- Скласти алгебраїчні доповнення $A_(ij)$ кожного елемента матриці $A$ і записати матрицю $A_(n\times n)^(*)=\left(A_(ij) \right)$ зі знайдених додатків алгебри.
- Записати зворотну матрицю з урахуванням формули $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.
Матрицю $(A^(*))^T$ найчастіше називають приєднаної (взаємної, союзної) до матриці $A$.
Якщо рішення відбувається вручну, перший спосіб хороший лише для матриць порівняно невеликих порядків: другого (), третього (), четвертого (). Щоб знайти зворотну матрицю для матриці вищого ладу, використовуються інші методи. Наприклад, метод Гауса, який розглянуто у другій частині.
Приклад №1
Знайти матрицю, зворотну до матриці $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \ 1 & -9 & 0 \end(array) \right)$.
Так як всі елементи четвертого стовпця дорівнюють нулю, то $ Delta A = 0 $ (тобто матриця $ A $ є виродженою). Оскільки $\Delta A=0$, зворотної матриці до матриці $A$ немає.
Приклад №2
Знайти матрицю, зворотну до матриці $A=\left(\begin(array) (cc) -5 & 7 \ 9 & 8 \end(array)\right)$.
Використовуємо метод приєднаної матриці. Спочатку знайдемо визначник заданої матриці $A$:
$$ \Delta A=\left| \begin(array) (cc) -5 & 7\ 9 & 8 \end(array)\right|=-5\cdot 8-7\dot 9=-103. $$
Так як $ \ Delta A \ neq 0 $, то зворотна матриця існує, тому продовжимо рішення. Знаходимо додатки алгебри
\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\end(aligned)
Складаємо матрицю з додатків алгебри: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.
Транспонуємо отриману матрицю: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\ -9 & -5 \end(array)\right)$ (отримана матриця часто називається приєднаною чи союзною матрицею до матриці $A$). Використовуючи формулу $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, маємо:
$$ A^(-1)=\frac(1)(-103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right) =\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right) $$
Отже, зворотну матрицю знайдено: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\9/103 & 5/103 \end(array)\right) $. Щоб перевірити істинність результату, достатньо перевірити істинність однієї з рівностей: $A^(-1)\cdot A=E$ або $A\cdot A^(-1)=E$. Перевіримо виконання рівності $A^(-1)\cdot A=E$. Щоб поменше працювати з дробами, підставлятимемо матрицю $A^(-1)$ не у формі $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$, а у вигляді $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\ -9 & -5 \end(array )\right)$:
Відповідь: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array)\right)$.
Приклад №3
Знайти зворотну матрицю для матриці $A=\left(\begin(array) (ccc) 1 & 7 & 3 -4 & 9 & 4 \0 & 3 & 2\end(array) \right)$.
Почнемо з обчислення визначника матриці $A$. Отже, визначник матриці $A$ такий:
$$ \Delta A=\left| \begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right| = 18-36 +56-12 = 26. $$
Так як $ \ Delta A \ neq 0 $, то зворотна матриця існує, тому продовжимо рішення. Знаходимо додатки алгебри кожного елемента заданої матриці:

Складаємо матрицю з додатків алгебри і транспонуємо її:
$$ A^*=\left(\begin(array) (ccc) 6 & 8 & -12 \ -5 & 2 & -3 \\ 1 & -16 & 37\end(array) \right); \; (A^*)^T=\left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right) $$
Використовуючи формулу $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, отримаємо:
$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$
Отже, $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6/13 & -3/26 & 37/26 \end(array) \right)$. Щоб перевірити істинність результату, достатньо перевірити істинність однієї з рівностей: $A^(-1)\cdot A=E$ або $A\cdot A^(-1)=E$. Перевіримо виконання рівності $A\cdot A^(-1)=E$. Щоб поменше працювати з дробами, будемо підставляти матрицю $A^(-1)$ не у формі $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 \end(array) \right)$, а у вигляді $\frac(1)(26)\cdot \left( \begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)$:
Перевірку пройдено успішно, зворотна матриця $A^(-1)$ знайдена правильно.
Відповідь: $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.
Приклад №4
Знайти матрицю, зворотну матриці $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \7 & 5 & 3 & 7 \\ 8 & -8 & -3 \end(array) \right)$.
Для матриці четвертого порядку знаходження зворотної матриці за допомогою додатків алгебри дещо важко. Проте такі приклади у контрольних роботах зустрічаються.
Щоб знайти зворотну матрицю, спочатку потрібно обчислити визначник матриці $A$. Найкраще в цій ситуації це зробити за допомогою розкладання визначника по рядку (стовпцю). Вибираємо будь-який рядок або стовпець і знаходимо додатки алгебри кожного елемента обраного рядка або стовпця.
Подібні на зворотні за багатьма властивостями.
Енциклопедичний YouTube
1 / 5
✪ Як знаходити зворотну матрицю - bezbotvy
✪ Зворотна матриця (2 способи знаходження)
✪ Зворотня матриця #1
✪ 2015-01-28. Зворотня матриця 3x3
✪ 2015-01-27. Зворотня матриця 2х2
Субтитри
Властивості зворотної матриці
- det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), де det (\displaystyle \ \det )позначає визначник.
- (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1))для двох квадратних оборотних матриць A (\displaystyle A)і B (\displaystyle B).
- (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), де (. . .) T (\displaystyle (...)^(T))позначає транспоновану матрицю.
- (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1))для будь-якого коефіцієнта k ≠ 0 (\displaystyle k\not = 0).
- E − 1 = E (\displaystyle \ E^(-1)=E).
- Якщо необхідно вирішити систему лінійних рівнянь , (b - ненульовий вектор) де x (\displaystyle x)- Шуканий вектор, і якщо A − 1 (\displaystyle A^(-1))існує, то x = A − 1 b (\displaystyle x=A^(-1)b). В іншому випадку або розмірність простору рішень більша за нуль, або їх немає зовсім.
Способи знаходження зворотної матриці
Якщо матриця оборотна, то для знаходження зворотної матриці можна скористатися одним із наступних способів:
Точні (прямі) методи
Метод Гауса-Жордана
Візьмемо дві матриці: саму Aта одиничну E. Наведемо матрицю Aдо одиничної матриці методом Гаусса-Жордана застосовуючи перетворення по рядках (можна також застосовувати перетворення і по стовпцях, але не в перемішування). Після застосування кожної операції до першої матриці застосуємо ту саму операцію до другої. Коли приведення першої матриці до одиничного вигляду буде завершено, друга матриця виявиться рівною. A −1.
При використанні методу Гауса перша матриця збільшуватиметься зліва на одну з елементарних матриць Λ i (\displaystyle \Lambda _(i))(трансвекцію або діагональну матрицю з одиницями на головній діагоналі, крім однієї позиції):
Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \Rightarrow \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 – a m − 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 – a m + 1 m / a m m … 0 … 0 … 0 − a n m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\dots &0\\ &&&\dots &&&\\0&\dots &1&-a_(m-1m)/a_(mm)&0&\dots &0\\0&\dots &0&1/a_(mm)&0&\dots &0\\0&\dots &0&-a_( m+1m)/a_(mm)&1&\dots &0\\&&&\dots &&&\\0&\dots &0&-a_(nm)/a_(mm)&0&\dots &1\end(bmatrix))).Друга матриця після застосування всіх операцій дорівнюватиме Λ (\displaystyle \Lambda )тобто буде шуканою. Складність алгоритму - O (n 3) (\displaystyle O(n^(3))).
За допомогою матриці додатків алгебри
Матриця, обернена матриці A (\displaystyle A), представна у вигляді
A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))
де adj (A) (\displaystyle (\mbox(adj))(A))- приєднана матриця;
Складність алгоритму залежить від складності алгоритму розрахунку визначника O det і дорівнює O(n²) · O det.
Використання LU/LUP-розкладання
Матричне рівняння A X = I n (\displaystyle AX = I_(n))для зворотної матриці X (\displaystyle X)можна розглядати як сукупність n (\displaystyle n)систем виду A x = b (\displaystyle Ax = b). Позначимо i (\displaystyle i)-ий стовпець матриці X (\displaystyle X)через X i (\displaystyle X_(i)); тоді A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1, …, n (\displaystyle i = 1, \ ldots, n),оскільки i (\displaystyle i)-м стовпцем матриці I n (\displaystyle I_(n))є одиничний вектор e i (\displaystyle e_(i)). іншими словами, перебування зворотної матриці зводиться до розв'язання n рівнянь з однією матрицею та різними правими частинами. Після виконання LUP-розкладання (час O(n³)) на розв'язання кожного з n рівнянь потрібен час O(n²), так що і ця частина роботи потребує часу O(n³).
Якщо матриця A невироджена, то нею можна розрахувати LUP-разложение P A = L U (\displaystyle PA = LU). Нехай P A = B (\displaystyle PA = B), B − 1 = D (\displaystyle B^(-1)=D). Тоді із властивостей зворотної матриці можна записати: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Якщо помножити цю рівність на U і L можна отримати дві рівності виду U D = L − 1 (\displaystyle UD=L^(-1))і DL = U − 1 (\displaystyle DL=U^(-1)). Перша з цих рівностей є системою з n² лінійних рівнянь для n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2)))з яких відомі праві частини (з властивостей трикутних матриць). Друге представляє також систему з n² лінійних рівнянь для n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2)))з яких відомі праві частини (також із властивостей трикутних матриць). Разом вони є системою з n² рівностей. За допомогою цих рівностей можна реккурентно визначити всі n² елементів матриці D. Тоді з рівності (PA) −1 = A −1 P −1 = B −1 = D. отримуємо рівність A − 1 = DP (\displaystyle A^(-1)=DP).
У разі використання LU-розкладання не потрібно перестановки стовпців матриці D, але рішення може розійтися навіть якщо матриця A невироджена.
Складність алгоритму – O(n³).
Ітераційні методи
Методи Шульця
( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\sum _(i=0)^(n)\Psi _(k)^(i)\end(cases)))
Оцінка похибки
Вибір початкового наближення
Проблема вибору початкового наближення в аналізованих тут процесах ітераційного звернення матриць не дозволяє ставитися до них як до самостійних універсальних методів, що конкурують із прямими методами обігу, заснованими, наприклад, на LU-розкладанні матриць. Є деякі рекомендації щодо вибору U 0 (\displaystyle U_(0)), що забезпечують виконання умови ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (спектральний радіус матриці менше одиниці), що є необхідним та достатнім для збіжності процесу. Однак при цьому, по-перше, потрібно знати зверху оцінку спектра матриці, що звертається, A або матриці AT (\displaystyle AA^(T))(а саме, якщо A - симетрична позитивно визначена матриця та ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), то можна взяти U 0 = α E (\displaystyle U_(0)=(\alpha )E), де; якщо ж A - довільна невироджена матриця та ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), то вважають U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), де також α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); можна звичайно спростити ситуацію і, скориставшись тим, що ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), покласти U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). По-друге, за такого завдання початкової матриці немає гарантії, що ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|)буде малою (можливо, навіть виявиться ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), і високий порядок швидкості збіжності виявиться далеко ще не відразу.
Приклади
Матриця 2х2
A − 1 = [ a b c d ]− 1 = 1 det (A) [ d − b − c a ] = 1 a d − b c [ d − b − c a ] . (\displaystyle \mathbf (A) ^(-1)=(\begin(bmatrix)a&b\c&d\\end(bmatrix))^(-1)=(\frac (1)(\det(\mathbf (A))))(\begin(bmatrix)\,\,\,d&\!\!-b\-c&\,a\\end(bmatrix))=(\frac (1)(ad- bc))(\begin(bmatrix)\,\,\,d&\!\!-b\-c&\,a\\end(bmatrix)).)Звернення матриці 2х2 можливе лише за умови, що a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).
Знаходження зворотної матриці- завдання, яке найчастіше вирішується двома методами:
- методом додатків алгебри, при якому потрібно знаходити визначники і транспонувати матриці;
- методом виключення невідомих Гаусса, у якому потрібно проводити елементарні перетворення матриць (складати рядки, множити рядки одне й те число і т. буд.).
Для особливо допитливих існують інші методи, наприклад, метод лінійних перетворень. На цьому уроці розберемо три згадані методи та алгоритми знаходження зворотної матриці цими методами.
Зворотною матрицею А, називається така матриця
А
. (1)
Зворотною матрицею , яку потрібно знайти для цієї квадратної матриці А, називається така матриця
твір на яку матриці Аправоруч є одиничною матрицею, тобто,
. (1)
Одиничною матрицею називається діагональна матриця, яка має всі діагональні елементи рівні одиниці.
Теорема.Для кожної неособливої (невиродженої, несингулярної) квадратної матриці можна знайти зворотну матрицю, і до того ж лише одну. Для особливої (виродженої, сингулярної) квадратної матриці зворотна матриця немає.
Квадратна матриця називається неособливою(або невиродженою, несингулярною), якщо її визначник не дорівнює нулю, та особливою(або виродженою, сингулярною), якщо її визначник дорівнює нулю.
Зворотну матрицю можна знайти тільки для квадратної матриці. Звичайно, зворотна матриця також буде квадратною і того ж порядку, що і ця матриця. Матриця, на яку може бути знайдена зворотна матриця, називається оборотною матрицею.
Для зворотної матриці існує доречна аналогія зі зворотним числом. Для кожного числа a, не рівного нулю, існує таке число b, що твір aі bодно одиниці: ab= 1. Число bназивається зворотним для числа b. Наприклад, число 7 зворотним є число 1/7, оскільки 7*1/7=1.
Знаходження зворотної матриці методом додатків алгебри (союзної матриці)
Для неособливої квадратної матриці Азворотною є матриця
де - визначник матриці А, а - матриця, союзна з матрицею А.
Союзної з квадратною матрицею Aназивається матриця того ж порядку, елементами якої є доповнення алгебри відповідних елементів визначника матриці , транспонованої щодо матриці A. Таким чином, якщо

то 
і 
Алгоритм знаходження зворотної матриці методом додатків алгебри
1. Знайти визначник цієї матриці A. Якщо визначник дорівнює нулю, знаходження зворотної матриці припиняється, оскільки матриця вироджена і обернена не існує.
2. Знайти матрицю, транспоновану щодо A.
3. Обчислити елементи союзної матриці як доповнення алгебри мариці, знайденої на кроці 2.
4. Застосувати формулу (2): помножити число, обернене до визначника матриці Aна союзну матрицю, знайдену на кроці 4.
5. Перевірити отриманий на кроці 4 результат, помноживши цю матрицю Aна зворотну матрицю. Якщо добуток цих матриць дорівнює одиничній матриці, отже зворотна матриця була знайдена правильно. Інакше розпочати процес вирішення знову.
приклад 1.Для матриці
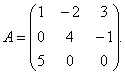
знайти зворотну матрицю.
Рішення. Для знаходження зворотної матриці необхідно знайти визначник матриці А. Знаходимо за правилом трикутників:

Отже, матриця А- Неособлива (невироджена, несингулярна) і для неї існує зворотна.
Знайдемо матрицю, союзну з цією матрицею А.
Знайдемо матрицю, транспоновану щодо матриці A:

Обчислюємо елементи союзної матриці як додатки алгебри матриці, транспонованої щодо матриці A:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Отже, матриця , союзна з матрицею A, має вигляд

Зауваження.Порядок обчислення елементів та транспонування матриці може бути іншим. Можна спочатку обчислити додатки алгебри матриці A, а потім транспонувати матрицю додатків алгебри. В результаті повинні вийти самі елементи союзної матриці.
Застосовуючи формулу (2), знаходимо матрицю, зворотну матриці А:

Знаходження зворотної матриці методом виключення невідомих Гаусса
Перший крок для знаходження зворотної матриці методом виключення невідомих Гаус - приписати до матриці Aодиничну матрицю того ж порядку, відокремивши їх вертикальною межею. Ми отримаємо здвоєну матрицю. Помножимо обидві частини цієї матриці на , тоді отримаємо
![]() ,
,
Алгоритм знаходження зворотної матриці методом виключення невідомих Гаусса
1. До матриці Aприписати одиничну матрицю того самого порядку.
2. Отриману здвоєну матрицю перетворити так, щоб у лівій її частині вийшла одинична матриця, тоді у правій частині на місці одиничної матриці автоматично вийде зворотна матриця. Матриця Aу лівій частині перетворюється на одиничну матрицю шляхом елементарних перетворень матриці.
2. Якщо у процесі перетворення матриці Aв одиничну матрицю в якомусь рядку або в якомусь стовпці виявляться тільки нулі, то визначник матриці дорівнює нулю, і, отже, матриця Aбуде виродженою, і вона не має зворотної матриці. І тут подальше перебування зворотної матриці припиняється.
приклад 2.Для матриці
знайти зворотну матрицю.

і будемо її перетворювати, так щоб у лівій частині вийшла поодинока матриця. Починаємо перетворення.
Помножимо перший рядок лівої та правої матриці на (-3) і складемо її з другим рядком, а потім помножимо перший рядок на (-4) і складемо її з третім рядком, тоді отримаємо
 .
.
Щоб по можливості не було дробових чисел при наступних перетвореннях, заздалегідь створимо одиницю в другому рядку в лівій частині здвоєної матриці. Для цього помножимо другий рядок на 2 і віднімемо з нього третій рядок, тоді отримаємо
 .
.
Складемо перший рядок з другим, а потім помножимо другий рядок на (-9) і складемо його з третім рядком. Тоді отримаємо
 .
.
Розділимо третій рядок на 8, тоді
 .
.
Помножимо третій рядок на 2 і складемо його з другим рядком. Виходить:
 .
.
Переставимо місцями другий та третій рядок, тоді остаточно отримаємо:
 .
.
Бачимо, що у лівій частині вийшла одинична матриця, отже, у правій частині вийшла зворотна матриця . Таким чином:
 .
.
Можна перевірити правильність обчислень, помножимо вихідну матрицю на знайдену матрицю зворотну:
В результаті повинна вийти зворотна матриця.
приклад 3.Для матриці
знайти зворотну матрицю.
Рішення. Складаємо здвоєну матрицю

і будемо її перетворювати.
Перший рядок множимо на 3, а другий на 2, і віднімаємо з другого, а потім перший рядок множимо на 5, а третій на 2 і віднімаємо з третього рядка, тоді отримаємо
 .
.
Перший рядок множимо на 2 і складаємо його з другого, а потім з третього рядка віднімаємо другий, тоді отримаємо
 .
.
В третьому рядку в лівій частині всі елементи вийшли рівними нулю. Отже, матриця вироджена та зворотної матриці не має. Подальше перебування зворотної мариці припиняємо.
Знаходження зворотної матриці.
У цій статті розберемося з поняттям зворотної матриці, її властивостями та способами знаходження. Детально зупинимося на рішенні прикладів, у яких потрібно побудувати зворотну матрицю для заданої.
Навігація на сторінці.
Зворотна матриця – визначення.
Знаходження зворотної матриці за допомогою матриці з додатків алгебри.
Властивості зворотної матриці.
Знаходження зворотної матриці методом Гаусса-Жордана.
Знаходження елементів зворотної матриці за допомогою розв'язання відповідних систем лінійних рівнянь алгебри.
Зворотна матриця – визначення.
Поняття зворотної матриці вводиться лише квадратних матриць, визначник яких відмінний від нуля, тобто для невироджених квадратних матриць.
Визначення.
Матрицяназивається зворотною для матриці, визначник якої відмінний від нуля , якщо справедливі рівність ![]() , де E- Поодинока матриця порядку nна n.
, де E- Поодинока матриця порядку nна n.
Знаходження зворотної матриці за допомогою матриці з додатків алгебри.
Як знайти зворотну матрицю для цієї?
По-перше, нам знадобляться поняття транспонованої матриці, мінору матриці та алгебраїчного доповнення елемента матриці.
Визначення.
Мінорk-ого порядкуматриці Aпорядку mна n- Це визначник матриці порядку kна kяка виходить з елементів матриці А, що знаходяться у вибраних kрядках та kстовпці. ( kне перевищує найменшого з чисел mабо n).
Мінор (n-1)-огопорядку, що складається з елементів усіх рядків, крім i-ий, і всіх стовпців, крім j-огоквадратної матриці Апорядку nна nпозначимо як .
Іншими словами, мінор виходить із квадратної матриці Апорядку nна nвикреслюванням елементів i-ийрядки та j-огостовпця.
Для прикладу запишемо, мінор Другогопорядку, що виходить з матриці  вибором елементів її другого, третього рядків та першого, третього стовпців
вибором елементів її другого, третього рядків та першого, третього стовпців  . Також покажемо мінор, який виходить із матриці
. Також покажемо мінор, який виходить із матриці  викресленням другого рядка та третього стовпця
викресленням другого рядка та третього стовпця  . Проілюструємо побудову цих мінорів: і .
. Проілюструємо побудову цих мінорів: і .
Визначення.
Алгебраїчним доповненнямелемента квадратної матриці називають мінор (n-1)-огопорядку, який виходить із матриці А, викресленням елементів її i-ийрядки та j-огостовпця, помножений на .
Алгебраїчне доповнення елемента позначається як . Таким чином, ![]() .
.
Наприклад, для матриці  Алгебраїчне доповнення елемента є.
Алгебраїчне доповнення елемента є.
По-друге, нам знадобляться дві властивості визначника, які ми розібрали у розділі обчислення визначника матриці:

На підставі цих властивостей визначника, визначення операції множення матриці на числоі поняття зворотної матриці справедлива рівність  , де - транспонована матриця, елементами якої є додатки алгебри .
, де - транспонована матриця, елементами якої є додатки алгебри .
Матриця  дійсно є зворотною для матриці А, оскільки виконуються рівності
дійсно є зворотною для матриці А, оскільки виконуються рівності ![]() . Покажемо це
. Покажемо це 

Складемо алгоритм знаходження зворотної матриціз використанням рівності  .
.
Розберемо алгоритм знаходження зворотної матриці з прикладу.
приклад.
Дано матрицю  . Знайдіть зворотну матрицю.
. Знайдіть зворотну матрицю.
Рішення.
Обчислимо визначник матриці А, Розклавши його за елементами третього стовпця: 
Визначник відмінний від нуля, тому матриця Аоборотна.
Знайдемо матрицю з додатків алгебри: 
Тому 
Виконаємо транспонування матриці з додатків алгебри: 
Тепер знаходимо зворотну матрицю як  :
:
Перевіряємо отриманий результат: 

Рівності ![]() виконуються, отже, зворотна матриця знайдена правильно.
виконуються, отже, зворотна матриця знайдена правильно.
Властивості зворотної матриці.
Поняття зворотної матриці, рівність  , визначення операцій над матрицями та властивості визначника матриці дозволяють обґрунтувати наступні властивості зворотної матриці:
, визначення операцій над матрицями та властивості визначника матриці дозволяють обґрунтувати наступні властивості зворотної матриці:
Знаходження елементів зворотної матриці за допомогою розв'язання відповідних систем лінійних рівнянь алгебри.
Розглянемо ще один спосіб знаходження зворотної матриці для квадратної матриці Апорядку nна n.
Цей метод заснований на вирішенні nсистем лінійних неоднорідних алгебраїчних рівнянь з nневідомими. Невідомими змінними цих системах рівнянь є елементи зворотної матриці.
Ідея дуже проста. Позначимо зворотну матрицю як X, тобто,  . Так як за визначенням зворотної матриці, то
. Так як за визначенням зворотної матриці, то 
Прирівнюючи відповідні елементи по стовпцям, отримаємо nсистем лінійних рівнянь 
Вирішуємо їх у будь-який спосіб і зі знайдених значень складаємо зворотну матрицю.
Розберемо цей спосіб з прикладу.
приклад.
Дано матрицю  . Знайдіть зворотну матрицю.
. Знайдіть зворотну матрицю.
Рішення.
Приймемо  . Рівність дає нам три системи лінійних неоднорідних рівнянь алгебри:
. Рівність дає нам три системи лінійних неоднорідних рівнянь алгебри: 
Не розписуватимемо рішення цих систем, при необхідності звертайтеся до розділу вирішення систем лінійних рівнянь алгебри.
З першої системи рівнянь маємо, з другої -, з третьої -. Отже, потрібна зворотна матриця має вигляд  . Рекомендуємо перевірити, щоб переконатися в правильності результату.
. Рекомендуємо перевірити, щоб переконатися в правильності результату.
Підведемо підсумок.
Ми розглянули поняття зворотної матриці, її властивості та три методи її знаходження.
Приклад рішень методом зворотної матриці
Завдання 1.Вирішити СЛАУ методом зворотної матриці. 2 x 1 + 3x 2 + 3x 3 + x 4 = 1 3 x 1 + 5x 2 + 3x 3 + 2x 4 = 2 5 x 1 + 7x 2 + 6x 3 + 2x 4 = 3 4 x 1 + 4x 2 + 3x 3 + х 4 = 4
Початок форми
Кінець форми
Рішення. Запишемо матрицю у вигляді: Вектор B: B T = (1,2,3,4) Головний визначник Мінор для (1,1): = 5 (6 1-3 2)-7 (3 1-3 2)+4 ( 3 2-6 2) = -3 Мінор для (2,1): = 3 (6 1-3 2)-7 (3 1-3 1)+4 (3 2-6 1) = 0 Мінор для (3 ,1): = 3 (3 1-3 2)-5 (3 1-3 1)+4 (3 2-3 1) = 3 Мінор для (4,1): = 3 (3 2-6 2) -5 (3 2-6 1)+7 (3 2-3 1) = 3 Визначник мінору ∆ = 2 (-3)-3 0+5 3-4 3 = -3
Транспонована матрицяАлгебраїчні доповнення ∆ 1,1 = 5 (6 1-2 3)-3 (7 1-2 4)+2 (7 3-6 4) = -3 ∆ 1,2 = -3 (6 1-2 3) -3 (7 1-2 4)+1 (7 3-6 4) = 0 ∆ 1,3 = 3 (3 1-2 3)-3 (5 1-2 4)+1 (5 3-3 4 ) = 3 ∆ 1,4 = -3 (3 2-2 6)-3 (5 2-2 7)+1 (5 6-3 7) = -3 ∆ 2,1 = -3 (6 1-2 3)-3 (5 1-2 4)+2 (5 3-6 4) = 9 ∆ 2,2 = 2 (6 1-2 3)-3 (5 1-2 4)+1 (5 3- 6 4) = 0 ∆ 2,3 = -2 (3 1-2 3)-3 (3 1-2 4)+1 (3 3-3 4) = -6 ∆ 2,4 = 2 (3 2- 2 6)-3 (3 2-2 5)+1 (3 6-3 5) = 3 ∆ 3,1 = 3 (7 1-2 4)-5 (5 1-2 4)+2 (5 4 -7 4) = -4 ∆ 3,2 = -2 (7 1-2 4)-3 (5 1-2 4)+1 (5 4-7 4) = 1 ∆ 3,3 = 2 (5 1 -2 4)-3 (3 1-2 4)+1 (3 4-5 4) = 1 ∆ 3,4 = -2 (5 2-2 7)-3 (3 2-2 5)+1 ( 3 7-5 5) = 0 ∆ 4,1 = -3 (7 3-6 4)-5 (5 3-6 4)+3 (5 4-7 4) = -12 ∆ 4,2 = 2 ( 7 3-6 4)-3 (5 3-6 4)+3 (5 4-7 4) = -3 ∆ 4,3 = -2 (5 3-3 4)-3 (3 3-3 4) +3 (3 4-5 4) = 9 ∆ 4,4 = 2 (5 6-3 7)-3 (3 6-3 5)+3 (3 7-5 5) = -3 Зворотна матриця Вектор результатів X X = A -1 ∙ B  X T = (2,-1,-0.33,1) x 1 = 2 x 2 = -1 x 3 = -0.33 x 4 = 1
X T = (2,-1,-0.33,1) x 1 = 2 x 2 = -1 x 3 = -0.33 x 4 = 1
Див. також рішень СЛАУ методом зворотної матриці online. Для цього введіть свої дані та отримайте рішення з докладними коментарями.
Завдання 2. Систему рівнянь записати у матричній формі та вирішити її за допомогою зворотної матриці. Зробити перевірку одержаного рішення. Рішення:xml:xls
Приклад 2. Записати систему рівнянь у матричній формі та вирішити за допомогою зворотної матриці. Рішення:xml:xls
приклад. Дано систему трьох лінійних рівнянь із трьома невідомими. Потрібно: 1) знайти її рішення за допомогою формул Крамера; 2) записати систему в матричній формі та вирішити її засобами матричного обчислення. Методичні рекомендації. Після рішення методом Крамера знайдіть кнопку "Рішення методом зворотної матриці для вихідних даних". Ви отримаєте відповідне рішення. Таким чином, дані знову заповнювати не доведеться. Рішення. Позначимо через А - матрицю коефіцієнтів за невідомих; X - матрицю-стовпець невідомих; B - матрицю-стовпець вільних членів:
|
|
Вектор B: B T =(4,-3,-3) З урахуванням цих позначень дана система рівнянь набуває наступної матричної форми: А*Х = B. Якщо матриця А - невироджена (її визначник відмінний від нуля, то вона має зворотну матрицю А -1 Помноживши обидві частини рівняння на А -1 отримаємо: А -1 * А * Х = А -1 * B, А -1 * А = Е. Ця рівність називається матричним записом розв'язання системи лінійних рівнянь. Для знаходження рішення системи рівнянь необхідно обчислити обернену матрицю А-1. Система матиме рішення, якщо визначник матриці A відмінний від нуля. Знайдемо головний визначник. ∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14 Отже, визначник 14 ≠ 0, тому продовжуємо Рішення. Для цього знайдемо зворотну матрицю через додатки алгебри. Нехай маємо невироджену матрицю А:
|
|
Обчислюємо додатки алгебри.
|
|
∆ 1,1 =(-2 (-1)-1 1)=1
|
|
∆ 1,2 =-(3 (-1)-0 1)=3
|
|
∆ 1,3 =(3 1-0 (-2))=3
|
|
∆ 2,1 =-(3 (-1)-1 2)=5
|
|
∆ 2,2 =(-1 (-1)-0 2)=1
|
|
∆ 2,3 =-(-1 1-0 3)=1
|
|
∆ 3,1 =(3 1-(-2 2))=7
|
|
∆ 3,2 =-(-1 1-3 2)=7
|
|
|
|
|
|
X T = (-1,1,2) x 1 = -14 / 14 = -1 x 2 = 14 / 14 = 1 x 3 = 28 / 14 = 2 Перевірка. -1 -1+3 1+0 2=4 3 -1+-2 1+1 2=-3 2 -1+1 1+-1 2=-3 doc:xml:xls Відповідь: -1,1,2.



