Зворотна матриця до матриці онлайн. Матрична алгебра – зворотна матриця

Знаходження зворотної матриці- завдання, яке найчастіше вирішується двома методами:

• методом додатків алгебри, при якому потрібно знаходити визначники і транспонувати матриці;
• методом виключення невідомих Гаусса, у якому потрібно проводити елементарні перетворення матриць (складати рядки, множити рядки одне й те число і т. буд.).

Для особливо допитливих існують інші методи, наприклад, метод лінійних перетворень. На цьому уроці розберемо три згадані методи та алгоритми знаходження зворотної матриці цими методами.

Зворотною матрицею А, називається така матриця

А
. (1)

Зворотною матрицею , яку потрібно знайти для цієї квадратної матриці А, називається така матриця

твір на яку матриці Аправоруч є одиничною матрицею, тобто,
. (1)

Одиничною матрицею називається діагональна матриця, яка має всі діагональні елементи рівні одиниці.

Теорема.Для кожної неособливої ​​(невиродженої, несингулярної) квадратної матриці можна знайти зворотну матрицю, і до того ж лише одну. Для особливої ​​(виродженої, сингулярної) квадратної матриці зворотна матриця немає.

Квадратна матриця називається неособливою(або невиродженою, несингулярною), якщо її визначник не дорівнює нулю, та особливою(або виродженою, сингулярною), якщо її визначник дорівнює нулю.

Зворотну матрицю можна знайти тільки для квадратної матриці. Звичайно, зворотна матриця також буде квадратною і того ж порядку, що і ця матриця. Матриця, на яку може бути знайдена зворотна матриця, називається оборотною матрицею.

Для зворотної матриці існує доречна аналогія зі зворотним числом. Для кожного числа a, не рівного нулю, існує таке число b, що твір aі bодно одиниці: ab= 1. Число bназивається зворотним для числа b. Наприклад, число 7 зворотним є число 1/7, оскільки 7*1/7=1.

Знаходження зворотної матриці методом додатків алгебри (союзної матриці)

Для неособливої ​​квадратної матриці Азворотною є матриця

де - визначник матриці А, а - матриця, союзна з матрицею А.

Союзної з квадратною матрицею Aназивається матриця того ж порядку, елементами якої є доповнення алгебри відповідних елементів визначника матриці , транспонованої щодо матриці A. Таким чином, якщо

то

і

Алгоритм знаходження зворотної матриці методом додатків алгебри

1. Знайти визначник цієї матриці A. Якщо визначник дорівнює нулю, знаходження зворотної матриці припиняється, оскільки матриця вироджена і обернена не існує.

2. Знайти матрицю, транспоновану щодо A.

3. Обчислити елементи союзної матриці як доповнення алгебри мариці, знайденої на кроці 2.

4. Застосувати формулу (2): помножити число, обернене до визначника матриці Aна союзну матрицю, знайдену на кроці 4.

5. Перевірити отриманий на кроці 4 результат, помноживши цю матрицю Aна зворотну матрицю. Якщо добуток цих матриць дорівнює одиничній матриці, отже зворотна матриця була знайдена правильно. Інакше розпочати процес вирішення знову.

приклад 1.Для матриці

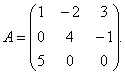
знайти зворотну матрицю.

Рішення. Для знаходження зворотної матриці необхідно знайти визначник матриці А. Знаходимо за правилом трикутників:

Отже, матриця А- Неособлива (невироджена, несингулярна) і для неї існує зворотна.

Знайдемо матрицю, союзну з цією матрицею А.

Знайдемо матрицю, транспоновану щодо матриці A:

Обчислюємо елементи союзної матриці як додатки алгебри матриці, транспонованої щодо матриці A:

Отже, матриця , союзна з матрицею A, має вигляд

Зауваження.Порядок обчислення елементів та транспонування матриці може бути іншим. Можна спочатку обчислити додатки алгебри матриці A, а потім транспонувати матрицю додатків алгебри. В результаті повинні вийти самі елементи союзної матриці.

Застосовуючи формулу (2), знаходимо матрицю, зворотну матриці А:

Знаходження зворотної матриці методом виключення невідомих Гаусса

Перший крок для знаходження зворотної матриці методом виключення невідомих Гаус - приписати до матриці Aодиничну матрицю того ж порядку, відокремивши їх вертикальною межею. Ми отримаємо здвоєну матрицю. Помножимо обидві частини цієї матриці на , тоді отримаємо

,

Алгоритм знаходження зворотної матриці методом виключення невідомих Гаусса

1. До матриці Aприписати одиничну матрицю того самого порядку.

2. Отриману здвоєну матрицю перетворити так, щоб у лівій її частині вийшла одинична матриця, тоді у правій частині на місці одиничної матриці автоматично вийде зворотна матриця. Матриця Aу лівій частині перетворюється на одиничну матрицю шляхом елементарних перетворень матриці.

2. Якщо у процесі перетворення матриці Aв одиничну матрицю в якомусь рядку або в якомусь стовпці виявляться тільки нулі, то визначник матриці дорівнює нулю, і, отже, матриця Aбуде виродженою, і вона не має зворотної матриці. І тут подальше перебування зворотної матриці припиняється.

приклад 2.Для матриці

знайти зворотну матрицю.

і будемо її перетворювати, так щоб у лівій частині вийшла поодинока матриця. Починаємо перетворення.

Помножимо перший рядок лівої та правої матриці на (-3) і складемо її з другим рядком, а потім помножимо перший рядок на (-4) і складемо її з третім рядком, тоді отримаємо

.

Щоб по можливості не було дробових чисел при наступних перетвореннях, заздалегідь створимо одиницю в другому рядку в лівій частині здвоєної матриці. Для цього помножимо другий рядок на 2 і віднімемо з нього третій рядок, тоді отримаємо

.

Складемо перший рядок з другим, а потім помножимо другий рядок на (-9) і складемо його з третім рядком. Тоді отримаємо

.

Розділимо третій рядок на 8, тоді

.

Помножимо третій рядок на 2 і складемо його з другим рядком. Виходить:

.

Переставимо місцями другий та третій рядок, тоді остаточно отримаємо:

.

Бачимо, що у лівій частині вийшла одинична матриця, отже, у правій частині вийшла зворотна матриця . Таким чином:

.

Можна перевірити правильність обчислень, помножимо вихідну матрицю на знайдену матрицю зворотну:

В результаті повинна вийти зворотна матриця.

приклад 3.Для матриці

знайти зворотну матрицю.

Рішення. Складаємо здвоєну матрицю

і будемо її перетворювати.

Перший рядок множимо на 3, а другий на 2, і віднімаємо з другого, а потім перший рядок множимо на 5, а третій на 2 і віднімаємо з третього рядка, тоді отримаємо

.

Перший рядок множимо на 2 і складаємо його з другого, а потім з третього рядка віднімаємо другий, тоді отримаємо

.

В третьому рядку в лівій частині всі елементи вийшли рівними нулю. Отже, матриця вироджена та зворотної матриці не має. Подальше перебування зворотної мариці припиняємо.

Ця тема є однією з найненависніших серед студентів. Гірше, мабуть, лише визначники.

Фішка в тому, що саме поняття зворотного елемента (і я зараз не лише про матриці) відсилає нас до операції множення. Навіть у шкільній програмі множення вважається складною операцією, а множення матриць — взагалі окрема тема, якій у мене присвячений цілий параграф і відеоурок.

Сьогодні ми не будемо вдаватися до подробиць матричних обчислень. Просто згадаємо: як позначаються матриці, як вони множаться і що з цього випливає.

Повторення: множення матриць

Насамперед домовимося про позначення. Матрицею $A$ розміру $\left[ m\times n \right]$ називається просто таблиця з чисел, в якій рівно $m$ рядків і $n$ стовпців:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

Щоб випадково не переплутати рядки та стовпці місцями (повірте, на іспиті можна і одиницю з двійкою переплутати — що вже казати про якісь там рядки), просто погляньте на картинку:

Що відбувається? Якщо розмістити стандартну систему координат $OXY$ у лівому верхньому кутку і направити осі так, щоб вони охоплювали всю матрицю, то кожній клітині цієї матриці можна однозначно зіставити координати $\left(x;y \right)$ - це і буде номер рядка і номер стовпця.

Чому система координат розміщена саме у лівому верхньому кутку? Бо саме звідти ми починаємо читати будь-які тексти. Це просто запам'ятати.

А чому вісь $x$ спрямована саме вниз, а не праворуч? Знову все просто: візьміть стандартну систему координат (вісь $x$ йде вправо, вісь $y$ вгору) і поверніть її так, щоб вона охоплювала матрицю. Це поворот на 90 градусів за годинниковою стрілкою – його результат ми й бачимо на картинці.

Загалом, як визначити індекси у елементів матриці, ми розібралися. Тепер розберемося з множенням.

Визначення. Матриці $A=\left[ m\times n \right]$ і $B=\left[ n\times k \right]$, коли кількість стовпців у першій збігається з кількістю рядків у другій, називаються узгодженими.

Саме у такому порядку. Можна сумніватися і сказати, мовляв, матриці $A$ і $B$ утворюють впорядковану пару $\left(A;B \right)$: якщо вони узгоджені в такому порядку, то необов'язково, що $B$ і $A$, тобто. пара $ \ left (B; A \ right) $ - теж узгоджена.

Помножувати можна лише узгоджені матриці.

Визначення. Твір узгоджених матриць $A=\left[m\times n\right]$ і $B=\left[n\times k \right]$ - це нова матриця $C=\left[m\times k \right]$ елементи якої $((c)_(ij))$ вважаються за формулою:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Іншими словами: щоб отримати елемент $((c)_(ij))$ матриці $C=A\cdot B$, потрібно взяти $i$-рядок першої матриці, $j$-й стовпець другої матриці, а потім попарно перемножити елементи з цього рядка та стовпця. Результати скласти.

Так, ось таке суворе визначення. З нього відразу випливає кілька фактів:

1. Множення матриць, взагалі кажучи, некомутативно: $ A \ cdot B \ ne B \ cdot A $;
2. Однак множення асоціативно: $ \ left (A cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ right) $;
3. І навіть дистрибутивно: $ \ left (A + B \ right) \ cdot C = A cdot C + B cdot C $;
4. І ще раз дистрибутивно: $ A \ cdot \ left (B + C \ right) = A \ cdot B + A \ cdot C $.

Дистрибутивність множення довелося окремо описувати для лівого та правого множника-суми якраз через некомутативність операції множення.

Якщо все ж таки виходить так, що $A cdot B = B cdot A $, такі матриці називаються перестановочними.

Серед усіх матриць, які там на щось множаться, є особливі ті, які при множенні на будь-яку матрицю $A$ знову дають $A$:

Визначення. Матриця $E$ називається одиничною, якщо $A\cdot E=A$ або $E\cdot A=A$. У випадку з квадратною матрицею $A$ можемо записати:

Поодинока матриця - частий гість під час вирішення матричних рівнянь. І взагалі найчастіший гість у світі матриць.:)

А ще через цю $E$ дехто вигадав всю ту дичину, яка буде написана далі.

Що таке зворотна матриця

Оскільки множення матриць - дуже трудомістка операція (доводиться перемножувати купу рядків і стовпців), то поняття зворотної матриці теж виявляється не найбільш очевидним. І потребує деяких пояснень.

Ключове визначення

Що ж, настав час пізнати істину.

Визначення. Матриця $B$ називається зворотною до матриці $A$ , якщо

Зворотна матриця позначається через $((A)^(-1))$ (не плутати зі ступенем!), тому визначення можна переписати так:

Здавалося б, все дуже просто і ясно. Але під час аналізу такого визначення відразу виникає кілька питань:

1. Чи завжди є зворотна матриця? І якщо не завжди, то як визначити: коли вона існує, а коли ні?
2. А хто сказав, що така матриця одно? Раптом для деякої вихідної матриці $A$ знайдеться ціла юрба зворотних?
3. Як виглядають усі ці «зворотні»? І як, власне, їх рахувати?

Щодо алгоритмів обчислення – про це ми поговоримо трохи згодом. Але на інші питання відповімо зараз. Оформимо їх у вигляді окремих тверджень-лем.

Основні властивості

Почнемо з того, як у принципі має виглядати матриця $A$, щоб для неї існувала $((A)^(-1))$. Зараз ми переконаємося в тому, що обидві ці матриці повинні бути квадратними, причому одного розміру: $ \ left [n \ times n \ right] $.

Лемма 1 . Дана матриця $A$ і обернена їй $((A)^(-1))$. Тоді обидві ці матриці квадратні, причому однакового порядку $ n $.

Доведення. Все просто. Нехай матриця $A=\left[m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Оскільки добуток $A\cdot ((A)^(-1))=E$ за визначенням існує, матриці $A$ і $((A)^(-1))$ узгоджені у вказаному порядку:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( align)\]

Це прямий наслідок алгоритму перемноження матриць: коефіцієнти $n$ і $a$ є «транзитними» і мають бути рівними.

Водночас визначено і зворотне множення: $((A)^(-1))\cdot A=E$, тому матриці $((A)^(-1))$ і $A$ також узгоджені у вказаному порядку:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( align)\]

Отже, без обмеження спільності можемо вважати, що $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Однак згідно з визначенням $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, тому розміри матриць суворо збігаються:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Ось і виходить, що всі три матриці - $ A $, $ ((A) ^ (-1)) $ і $ E $ - є квадратними розміром $ \ left [n \ times n \ right] $. Лемма доведена.

Що ж, уже непогано. Ми, що оборотними бувають лише квадратні матриці. Тепер переконаємося, що зворотна матриця завжди одна.

Лемма 2 . Дана матриця $A$ і обернена їй $((A)^(-1))$. Тоді ця зворотна матриця єдина.

Доведення. Підемо від протилежного: нехай матриця $A$ має хоча б два екземпляри зворотних —$B$ і $C$. Тоді, згідно з визначенням, вірні такі рівності:

\[\begin(align) & A\cdot B=B\cdot A=E; \ & A \ cdot C = C \ cdot A = E. \\ \end(align)\]

З леми 1 ми укладаємо, що всі чотири матриці - $ A $, $ B $, $ C $ і $ E $ - є квадратними однакового порядку: $ \ left [n \ times n \ right] $. Отже, визначено твір:

Оскільки множення матриць асоціативно (але не комутативно!), ми можемо записати:

\\\\\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \ \ & B \ cdot A \ cdot C = B \ cdot \ left (A \ cdot C \ right) = B \ cdot E = B; \ & B \ cdot A \ cdot C = C = B \ Rightarrow B = C. \\ \end(align)\]

Отримали єдино можливий варіант: два екземпляри зворотної матриці рівні. Лемма доведена.

Наведені міркування майже дослівно повторюють доказ єдиність зворотного елемента всім дійсних чисел $b\ne 0$. Єдине істотне доповнення - облік розмірності матриць.

Втім, ми досі нічого не знаємо про те, чи квадратна матриця є оборотною. Тут нам на допомогу приходить визначник це ключова характеристика для всіх квадратних матриць.

Лемма 3 . Дано матрицю $A$. Якщо зворотна до неї матриця $((A)^(-1))$ існує, то визначник вихідної матриці відмінний від нуля:

\[\left| A \right|\ne 0\]

Доведення. Ми вже знаємо, що $A$ і $((A)^(-1))$ — квадратні матриці розміру $\left[ n\times n \right]$. Отже, кожної з них можна обчислити визначник: $\left| A \right|$ і $\left| ((A)^(-1)) \right|$. Проте визначник твору дорівнює твору визначників:

\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

Але згідно з визначенням $A\cdot ((A)^(-1))=E$, а визначник $E$ завжди дорівнює 1, тому

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E \right|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \end(align)\]

Добуток двох чисел дорівнює одиниці тільки в тому випадку, коли кожне з цих чисел відмінно від нуля:

\[\left| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Ось і виходить, що $ \ left | A \right|\ne 0$. Лемма доведена.

Насправді ця вимога є цілком логічною. Зараз ми розберемо алгоритм знаходження зворотної матриці - і стане зрозуміло, чому за нульового визначника ніякої зворотної матриці в принципі не може існувати.

Але для початку сформулюємо «допоміжне» визначення:

Визначення. Вироджена матриця - це квадратна матриця розміру $ \ left [n \ times n \ right] $, чий визначник дорівнює нулю.

Таким чином, ми можемо стверджувати, що будь-яка оборотна матриця є невиродженою.

Як знайти зворотну матрицю

Зараз розглянемо універсальний алгоритм знаходження зворотних матриць. Взагалі, існує два загальноприйняті алгоритми, і другий ми також сьогодні розглянемо.

Той, який буде розглянутий зараз, дуже ефективний для матриць розміру $ \ left [2 \ times 2 \ right] $ і - частково - розміру $ \ left [3 \ times 3 \ right] $. А ось починаючи з розміру $ \ left [4 \ times 4 \ right] $ його краще не застосовувати. Чому зараз самі все зрозумієте.

Алгебраїчні доповнення

Готуйтеся. Нині буде біль. Ні, не хвилюйтеся: до вас не йде красива медсестра у спідниці, панчохах з мереживом і не зробить укол у сідницю. Все куди прозаїчніше: до вас йдуть алгебраїчні доповнення та її Величність «Союзна Матриця».

Почнемо з головного. Нехай є квадратна матриця розміру $ A = \ left [n \ times n \ right] $, елементи якої іменуються $ ((a)_ (ij)) $. Тоді для кожного такого елемента можна визначити додаток алгебри:

Визначення. Алгебраїчне доповнення $((A)_(ij))$ до елемента $((a)_(ij))$, що стоїть у $i$-му рядку і $j$-му стовпці матриці $A=\left[ n \times n \right]$ - це конструкція виду

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Де $M_(ij)^(*)$ — визначник матриці, отриманої з вихідної $A$ викреслюванням того самого $i$-го рядка і $j$-го стовпця.

Ще раз. Додаток алгебри до елемента матриці з координатами $\left(i;j \right)$ позначається як $((A)_(ij))$ і вважається за схемою:

1. Спочатку викреслюємо з вихідної матриці $i$-рядок і $j$-й стовпець. Отримаємо нову квадратну матрицю і її визначник ми позначаємо як $M_(ij)^(*)$.
2. Потім множимо цей визначник на $((\left(-1 \right))^(i+j))$ — спочатку цей вираз може здатися мозковиносним, але по суті ми просто з'ясовуємо знак перед $M_(ij)^(*) $.
3. Вважаємо - отримуємо конкретне число. Тобто. Додаток алгебри — це саме число, а не якась нова матриця і т.д.

Саму матрицю $M_(ij)^(*)$ називають додатковим мінором до елемента $((a)_(ij))$. І в цьому сенсі наведене вище визначення алгебраїчного доповнення є окремим випадком складнішого визначення того, що ми розглядали в уроці про визначник.

Важливе зауваження. Загалом у «дорослій» математиці алгебраїчні доповнення визначаються так:

1. Беремо у квадратній матриці $k$ рядків і $k$ стовпців. На їх перетині вийде матриця розміру $ \ left [k \ times k \ right] $ - її визначник називається мінором порядку $ k $ і позначається $ ((M)_ (k)) $.
2. Потім викреслюємо ці «вибрані» $k$ рядків і $k$ стовпців. Знову вийде квадратна матриця - її визначник називається додатковим мінором і позначається $ M_(k) ^ (*) $.
3. Помножуємо $M_(k)^(*)$ на $((\left(-1 \right))^(t))$, де $t$ — це (ось зараз увага!) сума номерів усіх вибраних рядків та стовпців . Це і буде додаток алгебри.

Погляньте на третій крок: там взагалі сума $2k$ доданків! Інша річ, що для $k=1$ ми отримаємо лише 2 доданків — це будуть ті самі $i+j$ — «координати» елемента $((a)_(ij))$, для якого ми шукаємо алгебраїчне доповнення.

Таким чином, сьогодні ми використовуємо злегка спрощене визначення. Але як ми побачимо надалі, його виявиться більш ніж достатньо. Куди важливіша наступна штука:

Визначення. Союзна матриця $S$ до квадратної матриці $A=\left[ n\times n \right]$ — це нова матриця розміру $\left[ n\times n \right]$, яка виходить із $A$ заміною $(( a)_(ij))$ алгебраїчними доповненнями $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

Перша думка, що виникає в момент усвідомлення цього визначення - це скільки ж доведеться всього вважати! Розслабтеся: вважати доведеться, але не так вже й багато.

Що ж, все це дуже мило, але навіщо це потрібне? А ось навіщо.

Основна теорема

Повернемося трохи тому. Пам'ятайте, в Лемме 3 стверджувалося, що оборотна матриця $A$ завжди не вироджена (тобто її визначник відмінний від нуля: $ \ left | A \ right | \ ne 0 $).

Так ось, вірно і зворотне: якщо матриця $ A $ не вироджена, вона завжди оборотна. І навіть існує схема пошуку $((A)^(-1))$. Зацініть:

Теорема про зворотну матрицю. Нехай дана квадратна матриця $ A = \ left [n \ times n \ right] $, причому її визначник відмінний від нуля: $ \ left | A \right|\ne 0$. Тоді зворотна матриця $((A)^(-1))$ існує і вважається за формулою:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

А тепер — все те саме, але розбірливим почерком. Щоб знайти зворотну матрицю, потрібно:

1. Порахувати визначник $ \ left | A \right|$ і переконатися, що він відмінний від нуля.
2. Скласти союзну матрицю $S$, тобто. порахувати 100500 додатків алгебри $((A)_(ij))$ і розставити їх на місці $((a)_(ij))$.
3. Транспонувати цю матрицю $S$, а потім помножити її на деяке число $q=(1)/(\left|A \right|)\;$.

І все! Зворотну матрицю $((A)^(-1))$ знайдено. Давайте подивимося на приклади:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

Рішення. Перевіримо оборотність. Порахуємо визначник:

\[\left| A \right|=\left| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Визначник відмінний від нуля. Значить, матриця оборотна. Складемо союзну матрицю:

Порахуємо додатки алгебри:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5 \right|=-5; \\ ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3 \right|=3. \\ \end(align)\]

Зверніть увагу: визначники | 2 |, | 5 |, | 1 | та |3| - це саме визначники матриць розміру $ \ left [1 \ times 1 \ right] $, а не модулі. Тобто. якщо в визначниках стояли негативні числа, прибирати мінус не треба.

Отже, наша союзна матриця виглядає так:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]\]

Ну от і все. Завдання вирішено.

Відповідь. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\end(array) \right] \]

Рішення. Знову вважаємо визначник:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Визначник відмінний від нуля - матриця оборотна. А ось зараз буде найжорсткіша: треба порахувати аж 9 (дев'ять, мати їх!) алгебраїчних доповнень. І кожне з них міститиме визначник $\left[2\times 2\right]$. Полетіли:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \end(matrix)\]

Коротше, союзна матриця виглядатиме так:

Отже, зворотна матриця буде такою:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(array) \right]\]

Ось і все. Ось і відповідь.

Відповідь. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\end(array) \right ]$

Як бачите, наприкінці кожного прикладу ми виконували перевірку. У зв'язку з цим важливе зауваження:

Не лінуйтеся виконувати перевірку. Помножте вихідну матрицю на знайдену зворотну - має вийти $E$.

Виконати цю перевірку набагато простіше та швидше, ніж шукати помилку у подальших обчисленнях, коли, наприклад, ви вирішуєте матричне рівняння.

Альтернативний спосіб

Як я і говорив, теорема про зворотну матрицю чудово працює для розмірів $ \ left [2 \ times 2 \ right] $ і $ \ left [3 \ times 3 \ right] $ (в останньому випадку - вже не так вже й "прекрасно" »), а ось для матриць великих розмірів починається прямий смуток.

Але не переживайте: є альтернативний алгоритм, за допомогою якого можна незворушно знайти зворотну хоч для матриці $ \ left [10 \ times 10 \ right] $. Але, як це часто буває, для розгляду цього алгоритму нам знадобиться невелика теоретична вступна.

Елементарні перетворення

Серед різноманітних перетворень матриці є кілька особливих їх називають елементарними. Таких перетворень рівно три:

1. множення. Можна взяти $i$-й рядок (стовпець) і помножити його на будь-яке число $k\ne 0$;
2. Додавання. Додати до $i$-го рядка (стовпця) будь-який інший $j$-й рядок (стовпець), помножений на будь-яке число $k\ne 0$ (можна, звичайно, і $k=0$, але який у цьому сенс ? Нічого не зміниться ж).
3. Перестановка. Взяти $i$-ю і $j$-ю рядки (стовпці) і поміняти місцями.

Чому ці перетворення називаються елементарними (для великих матриць вони виглядають не такими вже елементарними) і чому їх лише три ці питання виходять за рамки сьогоднішнього уроку. Тому не вдаватимемося в подробиці.

Важливо інше: всі ці збочення ми повинні виконувати над приєднаною матрицею. Так, так: ви не дочули. Зараз буде ще одне визначення – останнє у сьогоднішньому уроці.

Приєднана матриця

Напевно, у школі ви вирішували системи рівнянь методом складання. Ну, там, відняти з одного рядка інший, помножити якийсь рядок на число - ось це все.

Так ось: зараз буде все те саме, але вже «по-дорослому». Чи готові?

Визначення. Нехай дана матриця $ A = \ left [n \ times n \ right] $ і одинична матриця $ E $ такого ж розміру $ n $. Тоді приєднана матриця $ \ left [ A \ left | E \right. \right]$ — це нова матриця розміру $\left[ n\times 2n \right]$, яка виглядає так:

\[\left[ A\left| E \right. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Коротше кажучи, беремо матрицю $A$, праворуч приписуємо до неї одиничну матрицю $E$ потрібного розміру, розділяємо їх вертикальною рисою для краси - ось вам і приєднана.

У чому прикол? А ось у чому:

Теорема. Нехай матриця $A$ оборотна. Розглянемо приєднану матрицю $ \ left [ A \ left | E \right. \right]$. Якщо за допомогою елементарних перетворень рядківпривести її до вигляду $ \ left [ E \ left | B \right. \right]$, тобто. шляхом множення, віднімання та перестановки рядків отримати з $A$ матрицю $E$ праворуч, то отримана зліва матриця $B$ - це зворотна до $A$:

\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B=((A)^(-1))\]

Ось так просто! Коротше кажучи, алгоритм знаходження зворотної матриці виглядає так:

1. Записати приєднану матрицю $\left[ A\left| E \right. \right]$;
2. Виконувати елементарні перетворення рядків доти, доки права замість $A$ не з'явиться $E$;
3. Зрозуміло, ліворуч теж щось з'явиться якась матриця $B$. Це і буде обернена;
4. PROFIT!:)

Звісно, ​​сказати набагато простіше, ніж зробити. Тому давайте розглянемо кілька прикладів: для розмірів $\left[ 3\times 3 \right]$ і $\left[ 4\times 4 \right]$.

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Рішення. Складаємо приєднану матрицю:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Оскільки останній стовпець вихідної матриці заповнений одиницями, віднімемо перший рядок з інших:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \endend(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Більше одиниць немає, окрім першого рядка. Але її ми не чіпаємо, інакше в третьому стовпці почнуть «розмножуватися» щойно прибрані одиниці.

Зате можемо відняти другий рядок двічі з останнього — отримаємо одиницю в нижньому лівому кутку:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 &-7 & 0 & -1 & 0 & 1 \endend(array) \right]\begin(matrix) \\ \downarrow \\ -2 \\end(matrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Тепер можна відняти останній рядок з першого і двічі з другого — таким чином ми «занулимо» перший стовпець:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \end(array) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\end(matrix)\to \ \ \ to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\end(array) \right] \\ \end(align)\]

Помножимо другий рядок на −1, а потім віднімемо його 6 разів з першого і додамо 1 раз до останнього:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\end (matrix) \to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\end(array) \right] \\ \end(align)\]

Залишилося лише поміняти місцями рядки 1 та 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\end(array) \right]\]

Готово! Праворуч - шукана зворотна матриця.

Відповідь. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\end(array) \right ]$

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\end(matrix) \right]\]

Рішення. Знову складаємо приєднану:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Трохи позалимаємо, потурбуємося від того, скільки зараз доведеться рахувати... і почнемо рахувати. Для початку «обнулили» перший стовпець, віднімаючи рядок 1 з рядків 2 та 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Спостерігаємо дуже багато «мінусів» у рядках 2—4. Помножимо всі три рядки на −1, а потім випалимо третій стовпець, віднімаючи рядок 3 з інших:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end (array) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array) \right] \\ \end(align)\]

Тепер саме час «підсмажити» останній стовпець вихідної матриці: віднімаємо рядок 4 з інших:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Фінальний кидок: «випалюємо» другий стовпець, віднімаючи рядок 2 з рядка 1 та 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array) \right] \\ \end(align)\]

І знову зліва одинична матриця, значить праворуч - зворотна.:)

Відповідь. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrix) \right]$

Зворотна матриця для цієї це така матриця, множення вихідної на яку дає одиничну матрицю: Обов'язковою і достатньою умовою наявності зворотної матриці є нерівність нулю детермінанта вихідної (що в свою чергу має на увазі, що матриця повинна бути квадратна). Якщо ж визначник матриці дорівнює нулю, її називають виродженою і така матриця немає зворотної. У вищій математиці обернені матриці мають важливе значення і застосовуються для вирішення ряду завдань. Наприклад, на знаходження зворотної матриціпобудовано матричний метод розв'язання систем рівнянь. Наш сервіс сайт дозволяє обчислювати зворотну матрицю онлайндвома методами: методом Гауса-Жордана та за допомогою матриці алгебраїчних доповнень. Перервий має на увазі велику кількість елементарних перетворень усередині матриці, другий - обчислення детермінанта та додатків алгебри до всіх елементів. Для обчислення визначника матриці онлайн ви можете скористатися іншим сервісом - Обчислення детермінанта матриці онлайн

Знайти зворотну матрицю на сайт

сайтдозволяє знаходити зворотну матрицю онлайншвидко та безкоштовно. На сайті здійсняться обчислення нашим сервісом і видається результат із докладним рішенням щодо знаходження зворотної матриці. Сервер завжди видає лише точну та правильну відповідь. У завданнях визначення зворотної матриці онлайн, необхідно, щоб визначник матрицібув відмінним від нуля, інакше сайтповідомить про неможливість знайти зворотну матрицю через рівність нуля визначника вихідної матриці. Завдання щодо знаходження зворотної матрицізустрічається у багатьох розділах математики, будучи одним із самих базових понять алгебри та математичним інструментом у прикладних завданнях. Самостійне визначення зворотної матрицівимагає значних зусиль, багато часу, обчислень та великої уважності, щоб не допустити описки або дрібної помилки у обчисленнях. Тому наш сервіс з знаходження зворотної матриці онлайнзначно полегшить вам завдання та стане незамінним інструментом для вирішення математичних завдань. навіть якщо ви знаходите зворотну матрицюМи рекомендуємо перевірити ваше рішення на нашому сервері. Введіть вашу вихідну матрицю у нас на Обчислення зворотної матриці онлайн і звірте вашу відповідь. Наша система ніколи не помиляється і знаходить зворотну матрицюзаданої розмірності в режимі онлайнмиттєво! На сайті сайтдопускаються символьні записи в елементах матриць, в цьому випадку зворотна матриця онлайнбуде представлена ​​у загальному символьному вигляді.

Продовжуємо розмову про дії з матрицями. А саме – під час вивчення даної лекції ви навчитеся знаходити зворотну матрицю. Навчіться. Навіть якщо з математикою важко.

Що таке зворотна матриця? Тут можна провести аналогію зі зворотними числами: розглянемо, наприклад, оптимістичне число 5 та зворотне число . Добуток цих чисел дорівнює одиниці: . З матрицями все схоже! Добуток матриці на зворотну їй матрицю дорівнює - одиничної матриціяка є матричним аналогом числової одиниці. Однак про все по порядку - спочатку вирішимо важливе практичне питання, а саме, навчимося цю зворотну матрицю знаходити.

Що необхідно знати та вміти для знаходження зворотної матриці? Ви повинні вміти вирішувати визначники. Ви повинні розуміти, що таке матрицята вміти виконувати деякі дії з ними.

Існує два основні методи знаходження зворотної матриці:
за допомогою алгебраїчних доповненьі за допомогою елементарних перетворень.

Сьогодні ми вивчимо перший, простіший спосіб.

Почнемо з найжахливішого та незрозумілого. Розглянемо квадратнуматрицю. Зворотну матрицю можна знайти за такою формулою:

Де - визначник матриці - транспонована матриця алгебраїчних доповнень відповідних елементів матриці .

Поняття зворотної матриці існує лише для квадратних матриць, матриць "два на два", "три на три" і т.д.

Позначення: Як ви вже, напевно, помітили, зворотна матриця позначається надрядковим індексом

Почнемо з найпростішого випадку - матриці "два на два". Найчастіше, звичайно, потрібно «три на три», але, настійно рекомендую вивчити просте завдання, щоб засвоїти загальний принцип рішення.

Приклад:

Знайти зворотну матрицю для матриці

Вирішуємо. Послідовність дій зручно розкласти за пунктами.

1) Спочатку знаходимо визначник матриці.

Якщо з розумінням цього дійства погано, ознайомтеся з матеріалом Як визначити обчислювач?

Важливо!Якщо визначник матриці дорівнює НУЛЮ– зворотної матриці НЕ ІСНУЄ.

У аналізованому прикладі, як з'ясувалося, отже, все гаразд.

2) Знаходимо матрицю мінорів.

Для вирішення нашого завдання не обов'язково знати, що таке мінор, проте бажано ознайомитися зі статтею Як визначити обчислювач.

Матриця мінорів має такі самі розміри, як і матриця, тобто в даному випадку.
Справа за малим, залишилося знайти чотири числа і поставити їх замість зірочок.

Повертаємось до нашої матриці
Спочатку розглянемо лівий верхній елемент:

Як знайти його мінор?
А робиться це так: ДУМКОВО викреслюємо рядок і стовпець, в якому знаходиться даний елемент:

Що залишилося і є мінором цього елемента, яке записуємо в нашу матрицю мінорів:

Розглядаємо наступний елемент матриці:

Подумки викреслюємо рядок і стовпець, у якому стоїть цей елемент:

Те, що залишилося, є мінор даного елемента, який записуємо в нашу матрицю:

Аналогічно розглядаємо елементи другого рядка та знаходимо їх мінори:


Готово.

Це просто. У матриці мінорів потрібно ЗМІНИТИ ЗНАКИу двох чисел:

Саме ці цифри, які я обвів у гурток!

- матриця алгебраїчних доповнень відповідних елементів матриці.

І всього лише...

4) Знаходимо транспоновану матрицю додатків алгебри.

– транспонована матриця додатків алгебри відповідних елементів матриці .

5) Відповідь.

Згадуємо нашу формулу
Все знайдено!

Таким чином, зворотна матриця:

Відповідь краще залишити у такому вигляді. НЕ ПОТРІБНОділити кожен елемент матриці на 2, тому що вийдуть дробові числа. Докладніше цей нюанс розглянуто в тій же статті Дії з матрицями.

Як перевірити рішення?

Необхідно здійснити матричне множення або

Перевірка:

Отримано вже згадану одинична матриця- це матриця з одиницями на головної діагоналіта нулями в інших місцях.

Таким чином, зворотну матрицю знайдено правильно.

Якщо провести дію, то в результаті також вийде одинична матриця. Це один з небагатьох випадків, коли множення матриць перестановочно, більш детальну інформацію можна знайти у статті Властивості операцій над матрицями. Матричні вирази. Також зауважте, що під час перевірки константа (дроб) виноситься вперед і обробляється наприкінці – після матричного множення. Це стандартний прийом.

Переходимо до найпоширенішого на практиці випадку – матриці «три на три»:

Приклад:

Знайти зворотну матрицю для матриці

Алгоритм такий самий, як і для випадку «два на два».

Зворотну матрицю знайдемо за формулою: де - транспонована матриця алгебраїчних доповнень відповідних елементів матриці .

1) Знаходимо визначник матриці.

Тут визначник розкритий по першому рядку.

Також не забуваємо, що , отже, все нормально - зворотна матриця існує.

2) Знаходимо матрицю мінорів.

Матриця мінорів має розмірність «три на три» , і нам потрібно знайти дев'ять чисел.

Я докладно розгляну пару мінорів:

Розглянемо наступний елемент матриці:

ДУМКОВО викреслюємо рядок і стовпець, в якому знаходиться даний елемент:

Чотири числа, що залишилися, записуємо в визначник «два на два»

Цей визначник «два на два» та є мінором даного елемента. Його потрібно обчислити:


Все, мінор знайдено, записуємо його в нашу матрицю мінорів:

Як ви, напевно, здогадалися, необхідно вирахувати дев'ять визначників «два на два». Процес, звичайно, моторошний, але випадок не найважчий, буває гіршим.

Ну і для закріплення – знаходження ще одного мінору у картинках:

Інші мінори спробуйте вирахувати самостійно.

Остаточний результат:
- матриця мінорів відповідних елементів матриці.

Те, що всі мінори вийшли негативними – чиста випадковість.

3) Знаходимо матрицю алгебраїчних доповнень.

У матриці мінорів необхідно ЗМІНИТИ ЗНАКИсуворо у таких елементів:

В даному випадку:

Знаходження зворотної матриці для матриці «чотири на чотири» не розглядаємо, оскільки таке завдання може дати лише викладач-садист (щоб студент вирахував один визначник «чотири на чотири» та 16 визначників «три на три»). У моїй практиці зустрівся лише один такий випадок, і замовник контрольної роботи заплатив за мої муки досить дорого.

У ряді підручників, методик можна зустріти дещо інший підхід до знаходження зворотної матриці, проте я рекомендую користуватися саме вищевикладеним алгоритмом рішення. Чому? Тому що ймовірність заплутатися в обчисленнях і знаках набагато менше.

Визначення 1:матриця називається виродженою, якщо її визначник дорівнює нулю.

Визначення 2:матриця називається невиродженою, якщо її визначник не дорівнює нулю.

Матриця "A" називається зворотною матрицеюякщо виконується умова A*A-1 = A-1 *A = E (одиничної матриці).

Квадратна матриця оборотна тільки в тому випадку, коли вона невироджена.

Схема обчислення зворотної матриці:

1) Обчислити визначник матриці "A", якщо ∆ A = 0, то зворотної матриці немає.

2) Знайти всі додатки алгебри матриці "A".

3) Скласти матрицю з додатків алгебри (Aij )

4) Транспонувати матрицю з додатків алгебри (Aij )T

5) Помножити транспоновану матрицю на число, зворотне визначнику цієї матриці.

6) Виконати перевірку:

На перший погляд, може здатися, що це складно, але насправді все дуже просто. Усі рішення ґрунтуються на простих арифметичних діях, головне при вирішенні не плутатися зі знаками "-" та "+", і не втрачати їх.

А тепер давайте разом з Вами розв'яжемо практичне завдання, обчисливши зворотну матрицю.

Завдання: знайти зворотну матрицю "A", представлену на малюнку нижче:

1. Перше, що потрібно зробити, це знайти визначник матриці "A":

Пояснення:

Ми спростили наш визначник, скориставшись його основними функціями. По-перше, ми додали до 2 і 3 рядків елементи першого рядка, помножені на одне число.

По-друге, ми змінили 2 і 3 стовпець визначника, і за його властивостями змінили знак перед ним.

По-третє, ми винесли загальний множник (-1) другого рядка, тим самим знову змінивши знак, і він став позитивним. Також ми спростили 3 рядок так само, як на початку прикладу.

У нас вийшов трикутний визначник, у якого елементи нижче діагоналі дорівнюють нулю, і за 7 властивістю він дорівнює добутку елементів діагоналі. У результаті ми отримали ∆ A = 26, отже зворотна матриця існує.

А11 = 1 * (3 +1) = 4

А12 = -1 * (9 +2) = -11

А13 = 1 * 1 = 1

А21 = -1 * (-6) = 6

А22 = 1 * (3-0) = 3

А23 = -1 * (1 +4) = -5

А31 = 1 * 2 = 2

А32 = -1 * (-1) = -1

А33 = 1 + (1 +6) = 7

3. Наступний крок - складання матриці з додатків:

5. Помножуємо цю матрицю на число, зворотне визначнику, тобто на 1/26:

6. Ну а тепер нам просто потрібно виконати перевірку:

У ході перевірки ми отримали одиничну матрицю, отже, рішення було виконане абсолютно правильно.

2 спосіб обчислення зворотної матриці.

1. Елементарне перетворення матриць

2. Зворотна матриця через елементарний перетворювач.

Елементарне перетворення матриць включає:

1. Множення рядка на число, що не дорівнює нулю.

2. Додаток до будь-якого рядка іншого рядка, помноженого на число.

3. Зміна місцями рядків матриці.

4. Застосовуючи ланцюжок елементарних перетворень, отримуємо іншу матрицю.

А -1 = ?

1. (A|E) ~ (E|A -1 )

2. A -1 * A = E

Розглянемо це практичному прикладі з дійсними числами.

Завдання:Знайти обернену матрицю.

Рішення:

Виконаємо перевірку:

Невелике роз'яснення щодо рішення:

Спочатку ми переставили 1 і 2 рядок матриці, потім помножили перший рядок (-1).

Після цього помножили перший рядок (-2) і склали з другим рядком матриці. Після цього помножили 2 рядок на 1/4.

Заключним етапом перетворень стало множення другого рядка на 2 та додатком з першого. В результаті зліва у нас вийшла одинична матриця, отже зворотна матриця - це матриця справа.

Після перевірки ми переконалися у правильності рішення.

Як ви бачите, обчислення зворотної матриці – це дуже просто.

Наприкінці цієї лекції хотілося б також приділити трохи часу властивостям такої матриці.