Вирішення складних логарифмічних нерівностей з різними підставами. Складні логарифмічні нерівності

Визначення логарифмунайпростіше записати математично:

Визначення логарифму можна записати й іншим способом:

Зверніть увагу на обмеження, які накладаються на основу логарифму ( a) і на підлогарифмічний вираз ( x). Надалі ці умови перетворяться на важливі обмеження для ОДЗ, які потрібно буде враховувати під час вирішення будь-якого рівняння з логарифмами. Отже, тепер крім стандартних умов, що призводять до обмежень на ОДЗ (позитивність виразів під корінням парних ступенів, не рівність знаменника нулю тощо), потрібно враховувати ще й такі умови:

Підлогарифмічний вираз може бути лише позитивним.
Заснування логарифму може бути лише позитивним і не рівним одиниці.

Зверніть увагу, що ні основа логарифму, ні підлогарифмічний вираз не можуть бути рівними нулю. Зверніть також увагу і те, що саме значення логарифму може приймати всі можливі значення, тобто. логарифм може бути позитивним, негативним та рівним нулю. У логарифмів є дуже багато різних властивостей, які випливають із властивостей ступенів та визначення логарифму. Перелічимо їх. Отже, властивості логарифмів:

Логарифм твору:

Логарифм дробу:

Винесення ступеня за знак логарифму:

Зверніть особливу увагу на ті з останніх перерахованих властивостей, в яких з'являється знак модуля після винесення ступеня. Не забувайте, що при винесенні парного ступеня за знак логарифму, під логарифмом або основою потрібно залишити знак модуля.

Інші корисні властивості логарифмів:

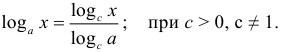
Остання властивість дуже часто застосовується у складних логарифмічних рівняннях та нерівностях. Його треба пам'ятати так само добре, як і решта, хоча про нього часто забувають.

Найпростіші логарифмічні рівняння мають вигляд:

А їхнє рішення задається формулою, яка безпосередньо випливає з визначення логарифму:

Інші найпростіші логарифмічні рівняння, це такі, які за допомогою алгебраїчних перетворень та наведених вище формул і властивостей логарифмів можна звести до вигляду:

Розв'язання таких рівнянь з урахуванням ОДЗ виглядає так:

Деякі інші логарифмічні рівняння зі змінною в основіможуть бути зведені до вигляду:

У таких логарифмічних рівняннях загальний вигляд рішення також безпосередньо випливає з визначення логарифму. Тільки в цьому випадку є додаткові обмеження для ОДЗ, які необхідно врахувати. У результаті, для вирішення логарифмічного рівняння зі змінною на підставі необхідно вирішувати таку систему:

При вирішенні складніших логарифмічних рівнянь, які не можна звести до одного з представлених вище рівнянь, також активно застосовується метод заміни змінних. Як завжди, застосовуючи цей метод слід пам'ятати, що після введення заміни рівняння має спроститися і більше не містити старої невідомої. Також потрібно не забувати виконувати зворотну заміну змінних.

Іноді при вирішенні логарифмічних рівнянь також доводиться використовувати графічний метод. Даний метод полягає в тому, щоб якомога точніше побудувати на одній координатній площині графіки функцій, які стоять у лівій та правій частинах рівняння, а потім знайти координати точок їх перетину по кресленню. Отримані у такий спосіб коріння обов'язково потрібно перевірити підстановкою в початкове рівняння.

При вирішенні логарифмічних рівнянь часто також корисний метод угруповання. При використанні цього методу головне пам'ятати, що: для того щоб добуток декількох множників дорівнював нулю, необхідно, щоб хоча б один з них дорівнював нулю, а решта існувала. Коли множниками є логарифми чи дужки з логарифмами, а чи не просто дужки зі змінними як і раціональних рівняннях, може виникнути багато помилок. Оскільки логарифми мають багато обмежень на ту область, де вони існують.

При вирішенні систем логарифмічних рівняньНайчастіше доводиться використовувати метод підстановки, або метод заміни змінних. Якщо є така можливість, то при вирішенні систем логарифмічних рівнянь потрібно прагнути до того, щоб кожне із рівнянь системи окремо призвести до такого виду, при якому можна буде здійснити перехід від логарифмічного рівняння до раціонального.

Найпростіші логарифмічні нерівності вирішуються приблизно як і аналогічні рівняння. Спочатку, за допомогою алгебраїчних перетворень і властивостей логарифмів, їх треба постаратися привести до такого виду, де у логарифмів у лівій та правій частині нерівності будуть однакові підстави, тобто. отримати нерівність виду:

Після чого потрібно перейти до раціональної нерівності, враховуючи, що цей перехід повинен бути виконаний наступним чином: якщо основа логарифму більша за одиницю, то знак нерівності змінювати не потрібно, а якщо основа логарифму менша за одиницю, то потрібно поміняти знак нерівності на протилежний (це означає змінити "менше" на "більше" або навпаки). При цьому знаки мінус на плюс, в обхід раніше вивчених правил, ніде міняти не потрібно. Запишемо математично те, що отримаємо внаслідок виконання такого переходу. Якщо основу більше одиниці отримаємо:

Якщо основа логарифму менше одиниці поміняємо знак нерівності і отримаємо таку систему:

Як бачимо при розв'язанні логарифмічних нерівностей, як зазвичай, враховується також і ОДЗ (це третя умова в системах вище). Причому в цьому випадку є можливість не вимагати позитивності обох підлогарифмічних виразів, а вимагати позитивності лише меншого з них.

При вирішенні логарифмічних нерівностей зі змінною на підставілогарифма необхідно самостійно розглядати обидва варіанти (коли основа менше одиниці, і більше одиниці) та об'єднувати рішення цих випадків у сукупність. У цьому слід пам'ятати і про ОДЗ, тобто. про те, що і основа, і всі підлогарифмічні вирази повинні бути позитивними. Таким чином, при розв'язанні нерівності виду:

Отримаємо таку сукупність систем:

Більш складні логарифмічні нерівності можуть вирішуватися за допомогою заміни змінних. Деякі інші логарифмічні нерівності (як і логарифмічні рівняння) для вирішення вимагають проведення процедури логарифмування обох частин нерівності або рівняння на однаковій підставі. Так ось при проведенні такої процедури з логарифмічними нерівностями є тонкість. Зверніть увагу, що при логарифмуванні на підставі більшій одиниці, знак нерівності не змінюється, а якщо основа менша за одиницю, то знак нерівності змінюється на протилежний.

Якщо логарифмічна нерівність не може бути зведена до раціонального або вирішена за допомогою заміни, то в цьому випадку слід застосовувати узагальнений метод інтервалів, Який полягає в наступному:

Визначте ОДЗ;
Перетворіть нерівність так, щоб у правій частині був нуль (у лівій частині, якщо це можливо, приведіть до спільного знаменника, розкладіть на множники тощо);
Знайдіть усі коріння чисельника і знаменника і нанесіть їх на числову вісь, причому, якщо нерівність не сувора, зафарбуйте коріння чисельника, ну а коріння знаменника у будь-якому випадку залиште виколотими точками;
Знайдіть знак всього виразу кожному з інтервалів, підставляючи в перетворене нерівність число з цього інтервалу. При цьому вже не можна ніяким чином чергувати знаки переходячи через точки на осі. Визначати знак виразу кожному інтервалі потрібно саме підстановкою значення з інтервалу у цей вираз, і так кожного інтервалу. Більше ніяк не можна (у цьому й полягає, за великим рахунком, відмінність узагальненого методу інтервалів від звичайного);
Знайдіть перетин ОДЗ і проміжків, що задовольняють нерівності, при цьому не втратите окремі точки, що задовольняють нерівності (корені чисельника в нестрогих нерівностях), і не забудьте виключити з відповіді всі корені знаменника у всіх нерівностях.

назад
Вперед

Як успішно підготуватися до ЦТ з фізики та математики?

Для того щоб успішно підготуватися до ЦТ з фізики та математики, серед іншого, необхідно виконати три найважливіші умови:

Вивчити всі теми та виконати всі тести та завдання наведені у навчальних матеріалах на цьому сайті. Для цього потрібно всього нічого, а саме: присвячувати підготовці до ЦТ з фізики та математики, вивченню теорії та вирішенню завдань по три-чотири години щодня. Справа в тому, що ЦТ це іспит де мало просто знати фізику чи математику, потрібно ще вміти швидко і без збоїв вирішувати велику кількість завдань з різних тем та різної складності. Останньому навчитися можна лише вирішивши тисячі завдань.
Вивчити всі формули та закони у фізиці, і формули та методи в математиці . Насправді, виконати це теж дуже просто, необхідних формул із фізики всього близько 200 штук, а з математики навіть трохи менше. У кожному з цих предметів є близько десятка стандартних методів вирішення завдань базового рівня складності, які теж цілком можна вивчити, і таким чином, абсолютно на автоматі і без труднощів вирішити в потрібний момент більшу частину ЦТ. Після цього Вам залишиться подумати лише над найскладнішими завданнями.
Відвідати всі три етапи репетиційного тестування з фізики та математики. Кожен РТ можна відвідувати по два рази, щоб вирішувати обидва варіанти. Знову ж таки на ЦТ, крім уміння швидко і якісно вирішувати завдання, і знання формул і методів необхідно також вміти правильно спланувати час, розподілити сили, а головне правильно заповнити бланк відповідей, не переплутавши ні номера відповідей і завдань, ні власне прізвище. Також у ході РТ важливо звикнути до стилю постановки питань у завданнях, що на ЦТ може здатися непідготовленій людині дуже незвичним.

Успішне, старанне та відповідальне виконання цих трьох пунктів дозволить Вам показати на ЦТ відмінний результат, максимальний з того, на що Ви здатні.

Знайшли помилку?

Якщо Ви, як Вам здається, знайшли помилку в навчальних матеріалах, напишіть, будь ласка, про неї на пошту. Написати про помилку можна також у соціальній мережі (). У листі вкажіть предмет (фізика чи математика), назву чи номер теми чи тесту, номер завдання, чи місце у тексті (сторінку) де на Вашу думку є помилка. Також опишіть у чому полягає ймовірна помилка. Ваш лист не залишиться непоміченим, помилка або буде виправлена, або Вам роз'яснять, чому це не помилка.

Нерівність називається логарифмічною, якщо в ній міститься логарифмічна функція.

Методи вирішення логарифмічних нерівностей не відрізняються від , крім двох речей.

По-перше, при переході від логарифмічної нерівності до нерівності підлогарифмічних функцій слід стежити за знаком нерівності, що виходить. Він підпорядковується такому правилу.

Якщо основа логарифмічної функції більша за $1$, то при переході від логарифмічної нерівності до нерівності підлогарифмічних функцій знак нерівності зберігається, а якщо менше $1$, то змінюється на протилежний.

По-друге, розв'язання будь-якої нерівності – проміжок, а, отже, наприкінці розв'язання нерівності підлогарифмічних функцій необхідно скласти систему з двох нерівностей: першою нерівністю цієї системи буде нерівність підлогарифмічних функцій, а другим – проміжок області визначення логарифмічних функцій, що входять до логарифмічної нерівності.

практика.

Вирішимо нерівності:

1. $\log_(2)((x+3)) \geq 3.$

$D(y): \ x+3>0.$

$x \in (-3;+\infty)$

Основа логарифму дорівнює $2>1$, тому знак не змінюється. Користуючись визначенням логарифму, отримаємо:

$x+3 \geq 2^(3),$

$x \in )