Збіжність і розбіжність невласних інтегралів. Приклади дослідження невласних інтегралів на збіжність

1. Невласні інтеграли з нескінченними межами

Згадаймо визначення інтеграла як межі інтегральних сум:

У визначенні передбачається, що інтервал інтегрування є кінцевим, а функція f (x) безперервна в ньому. Порушення цих припущень призводить до невласних інтегралів.

Визначення.Якщо інтеграл прагне кінцевої межі при необмеженому зростанні "b", то цю межу називають невласним інтегралом з нескінченним верхнім кордоном від функції f (x) і позначають символом

І тут кажуть, що невласний інтеграл існує чи сходиться.

Якщо вказана межа не існує або існує, але нескінченна, то кажуть, що інтеграл не існує або розходиться.

Аналогічно визначається невласний інтеграл із нескінченним нижнім кордоном:

Невласний інтеграл із двома нескінченними межами визначається формулою:

де с – будь-яка фіксована точка на осі Ох.

Отже, невласні інтеграли можуть бути з нескінченно нижнім кордоном, з нескінченно верхнім кордоном, а також з двома нескінченними кордонами.

Ознаки збіжності. Абсолютна та умовна збіжність

Інтеграл існує лише тоді, коли існує кожен із інтегралів: і .

приклад.Дослідити на збіжність інтеграл

Вважаючи з = 0, отримаємо:

тобто. інтеграл сходиться.

Іноді не потрібно обчислювати невласний інтеграл, а достатньо лише знати, сходиться він чи розходиться, порівнявши його з іншим інтегралом.

Теорема порівняння невласних інтегралів.

Нехай в інтервалі функція f (x) має декілька (кінцеве число) точок розриву першого роду, це "перешкода" легко усунути, розбивши відрізок точками розриву на кілька відрізків, обчислити певні інтеграли на кожній окремій ділянці та результати скласти.

Розглянемо певний інтеграл від функції, необмеженої при наближенні до одного з кінців відрізка, наприклад, .

(У таких випадках зазвичай кажуть: “Функція має нескінченний розрив на правому кінці відрізка інтегрування”.)

Зрозуміло, що звичайне визначення інтеграла тут втрачає сенс.

Визначення. Невласним інтегралом від функції f(x), безперервної при а?< b и неограниченной при x ® b - 0, называется предел:

Аналогічно визначається невласний інтеграл від функції, що має нескінченний розрив на лівому кінці відрізка:

Отже, дільниці [ -1, 0] інтеграл розходиться.

Отже, на ділянці інтеграл також розходиться.

Таким чином, даний інтеграл розходиться по всьому відрізку [-1, 1]. Зазначимо, що якби ми стали обчислювати цей інтеграл, не звертаючи уваги на розрив підінтегральної функції у точці x = 0, то отримали б неправильний результат. Справді,

, що неможливо.

Отже, на дослідження невласного інтеграла від розривної функції, необхідно " розбити " його кілька інтегралів і досліджувати їх.

Як відомо, знаходження інтеграла може бути досить складним завданням. Було б великим розчаруванням зайнятися обчисленням невласного інтеграла і виявити наприкінці шляху, що він розходиться. Тому цікаві методи, що дозволяють без серйозних обчислень по одному виду функцій зробити висновок про збіжність або розбіжність невласного інтеграла. Перша та друга теореми порівняння, які будуть розглянуті нижче, значною мірою допомагають досліджувати невласні інтеграли на збіжність.

Нехай f(x)?0. Тоді функції

є монотонно зростаючими від змінних t або-д (оскільки беремо д>0, -д прагне нуля зліва). Якщо при зростанні аргументів функції F1(t) і F2(-д) залишаються обмеженими зверху, це означає, що відповідні невласні інтеграли сходяться. На цьому ґрунтується перша теорема порівняння для інтегралів від невід'ємних функцій.

Нехай для функції f(x) та g(x) при x?a виконані умови:

• 1) 0?f(x)?g(x);
• 2) Функції f(x) та g(x) безперервні.

Тоді зі збіжності інтеграла випливає збіжність інтеграла, та якщо з розбіжності інтеграла слід розбіжність

Оскільки 0?f(x)?g(x) і функції безперервні, то

За умовою інтеграл сходиться, тобто. має кінцеву величину. Отже, інтеграл сходиться також.

Нехай тепер інтеграл розходиться. Припустимо, що інтеграл сходиться, але тоді має сходитися інтеграл, що суперечить умові. Наше припущення неправильне, інтеграл розходиться.

Теорема порівняння для невласних інтегралів 2-го роду.

Нехай для функцій f(x) і g(x) на проміжку необмежено зростає при x>+0. Для неї при x>+0 справедлива нерівність<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Теорема порівняння для невласних інтегралів 1-го роду.

Нехай функції f(x) і g(x) на проміжку , а відрізок інтегрування є кінцевим, тобто обмежений числами, а чи не нескінченністю. Деякі завдання призводять до необхідності відмовитися від цих обмежень. Так виникають невласні інтеграли.

Геометричний зміст невласного інтегралуз'ясовується досить легко. У разі, коли графік функції y = f(x) знаходиться вище осі Ox, певний інтеграл виражає площу криволінійної трапеції, обмеженою кривою y = f(x) , віссю абсцис та ординатами x = a , x = b. У свою чергу невласний інтеграл виражає площу необмеженої (нескінченної) криволінійної трапеції, укладеної між лініями y = f(x) (на малюнку нижче – червоного кольору), x = aі віссю абсцис.

Аналогічним чином визначаються невласні інтеграли й інших нескінченних інтервалів:

Площа нескінченної криволінійної трапеції може бути кінцевим числом і в цьому випадку невласний інтеграл називається схожим. Площа може бути і нескінченністю і в цьому випадку невласний інтеграл називається розбіжним.

Використання межі інтеграла замість найневласнішого інтеграла.Щоб обчислити невласний інтеграл, потрібно використовувати межу певного інтеграла. Якщо ця межа існує і кінцева (не дорівнює нескінченності), то невласний інтеграл називається схожим, а в іншому випадку - розбіжним. До чого прагне змінна під знаком межі, залежить від того, чи маємо ми справу з невласним інтегралом першого роду чи другого роду. Дізнаємося про це зараз.

Невласні інтеграли першого роду - з нескінченними межами та їхня схожість

Невласні інтеграли з нескінченною верхньою межею

Отже, запис невласного інтеграла відрізняється від звичайного певного інтеграла тим, що верхня межа інтегрування нескінченна.

Визначення. Невласним інтегралом з нескінченною верхньою межею інтегрування від безперервної функції f(x) на проміжку від a до ∞ називається межа інтеграла цієї функції з верхньою межею інтегрування b та нижньою межею інтегрування a за умови, що верхня межа інтегрування необмежено зростає, тобто.

.

Якщо ця межа існує і дорівнює деякому числу, а не нескінченності, то невласний інтеграл називається схожима число, якому дорівнює межа, приймається за його значення. В іншому випадку невласний інтеграл називається розбіжнимі йому не приписується жодного значення.

Приклад 1. Обчислити невласний інтеграл(якщо він сходиться).

Рішення. На підставі визначення невласного інтегралу знаходимо

Так як межа існує і дорівнює 1, то і даний невласний інтеграл сходитьсяі дорівнює 1.

У наступному прикладі підінтегральна функція майже як у прикладі 1, тільки ступінь ікса - не двійка, а літера альфа, а завдання полягає у дослідженні невласного інтеграла на збіжність. Тобто належить відповісти на запитання: за яких значень альфи цей невласний інтеграл сходиться, а за яких розходиться?

Приклад 2. Дослідити на збіжність невласний інтеграл(Нижня межа інтегрування більше нуля).

Рішення. Припустимо спочатку, що , тоді

В отриманому вираженні перейдемо до межі при:

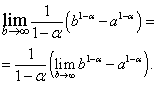
Неважко бачити, що межа у правій частині існує і дорівнює нулю, коли , тобто , і не існує, коли , тобто .

У першому випадку, тобто має місце . Якщо то і немає.

Висновок нашого дослідження наступний: даний невласний інтеграл сходитьсяпри і розходитьсяпри .

Застосовуючи до вивченого виду невласного інтеграла формулу Ньютона-Лейбніца , можна вивести наступну дуже схожу на неї формулу:

.

Це узагальнена формула Ньютона-Лейбніца.

Приклад 3. Обчислити невласний інтеграл(якщо він сходиться).

Межа цього інтегралу існує:

Другий інтеграл, що становить суму, що виражає вихідний інтеграл:

Межа цього інтеграла також існує:

.

Знаходимо суму двох інтегралів, що є значенням вихідного невласного інтеграла з двома нескінченними межами:

Невласні інтеграли другого роду - від необмежених функцій та їхня схожість

Нехай функція f(x) задана на відрізку від a до b і необмежена на ньому. Припустимо, що функція перетворюється на нескінченність у точці b , у той час як у всіх інших точках відрізка вона безперервна.

Визначення. Невласним інтегралом функції f(x) на відрізку від a до b називається межа інтеграла цієї функції з верхньою межею інтегрування c , якщо при прагненні c до b функція необмежено зростає, а точці x = b функція не визначена, тобто.

.

Якщо ця межа існує, то невласний інтеграл другого роду називається схожим, інакше - розбіжним.

Використовуючи формулу Ньютона-Лейбніца, виводимо.