Множення та розподіл раціональних чисел. Розмноження та розподіл алгебраїчних дробів

На цьому уроці будуть розглянуті правила множення та поділу алгебраїчних дробів, а також приклади застосування цих правил. Множення та розподіл алгебраїчних дробів не відрізняється від множення та поділу звичайних дробів. Разом з тим, наявність змінних призводить до більш складних способів спрощення отриманих виразів. Незважаючи на те, що множення та розподіл дробів виконується простіше, ніж їх складання та віднімання, до вивчення даної теми необхідно підійти вкрай відповідально, оскільки в ній існує багато «підводних каменів», на які зазвичай не звертають уваги. У рамках уроку ми не тільки вивчимо правила множення та розподілу дробів, але й розберемо нюанси, які можуть виникнути при їх застосуванні.

Тема:Алгебраїчні дроби. Арифметичні операції над алгебраїчними дробами

Урок:Розмноження та розподіл алгебраїчних дробів

Правила множення та розподілу алгебраїчних абсолютно аналогічні правилам множення та розподілу звичайних дробів. Нагадаємо їх:

Тобто для того, щоб помножити дроби, необхідно помножити їх чисельники (це буде чисельник твору), і помножити їх знаменники (це буде знаменник твору).

Поділ на дріб - це множення на перевернутий дріб, тобто, для того, щоб розділити два дроби, необхідно перший з них (ділене) помножити на перевернутий другий (ділитель).

Незважаючи на простоту даних правил, багато хто при вирішенні прикладів з цієї теми припускаються помилок у ряді окремих випадків. Розглянемо докладніше ці окремі випадки:

У всіх цих правилах ми скористалися наступним фактом: .

Вирішимо кілька прикладів на множення та розподіл звичайних дробів, щоб згадати, як користуватися вказаними правилами.

Приклад 1

Примітка:при скороченні дробів ми скористалися розкладанням числа на прості множники. Нагадаємо, що простими числами називаються такі натуральні числа, які поділяються тільки на і на себе. Інші числа називаються складовими . Число не відноситься ні до простих, ні до складових. Приклади простих чисел: .

Приклад 2

Розглянемо тепер один із окремих випадків із звичайними дробами.

Приклад 3

Як бачимо, множення та розподіл звичайних дробів, у разі правильного застосування правил, не є складним.

Розглянемо множення та розподіл алгебраїчних дробів.

Приклад 4

Приклад 5

Зазначимо, що скорочувати дроби після множення можна і навіть потрібно за тими самими правилами, які ми до цього розглядали на уроках, присвячених скороченню дробів алгебри. Розглянемо кілька простих прикладів на окремі випадки.

Приклад 6

Приклад 7

Розглянемо тепер кілька складніших прикладів на множення та розподіл дробів.

Приклад 8

Приклад 9

Приклад 10

Приклад 11

Приклад 12

Приклад 13

До цього розглядали дроби, у яких і чисельник, і знаменник були одночленами. Однак у ряді випадків необхідно перемножити або поділити дроби, чисельники та знаменники яких є багаточленами. У цьому випадку правила залишаються такими ж, а для скорочення необхідно використовувати формули скороченого множення та винесення за дужки.

Приклад 14

Приклад 15

Приклад 16

Приклад 17

Приклад 18

Насамперед, щоб навчитися працювати з раціональними дробами без помилок, необхідно вивчити формули скороченого множення. І не просто вивчити їх необхідно розпізнавати навіть тоді, коли в ролі доданків виступають синуси, логарифми і коріння.

Однак основним інструментом залишається розкладання чисельника та знаменника раціонального дробу на множники. Цього можна досягти трьома різними способами:

Власне, формула скороченого множення: вони дозволяють згорнути многочлен в один або кілька множників;
За допомогою розкладання квадратного тричлена на множники через дискримінант. Цей же спосіб дозволяє переконатися, що будь-який тричлен на множники взагалі не розкладається;
Метод угруповання — найскладніший інструмент, але це єдиний спосіб, який працює, якщо не спрацювали два попередні.

Як ви вже, напевно, здогадалися з назви цього відео, ми знову поговоримо про раціональні дроби. Буквально кілька хвилин тому у мене закінчилося заняття з одним десятикласником і там ми розбирали саме ці вирази. Тому цей урок буде призначений саме для старшокласників.

Напевно, у багатьох зараз виникне питання: «Навіщо учням 10-11 класів вивчати такі прості речі як раціональні дроби, адже це проходить у 8 класі?». Але в тому й біда, що більшість людей цю тему саме «проходять». Вони в 10-11 класі вже не пам'ятають, як робиться множення, розподіл, віднімання та складання раціональних дробів з 8-го класу, а саме на цих простих знаннях будуються подальші, складніші конструкції, як розв'язання логарифмічних, тригонометричних рівнянь та багатьох інших складних виразів, тому без раціональних дробів робити у старших класах практично нема чого.

Формули для вирішення завдань

Давайте перейдемо до справи. Насамперед нам знадобиться два факти — два комплекти формул. Насамперед, необхідно знати формули скороченого множення:

$((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right)$ - різниця квадратів;
$((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \right))^(2))$ — квадрат суми або різниці;
$((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b)^( 2)) \right)$ - сума кубів;
$((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+((b)^(2) ) \right)$ - Різниця кубів.

У чистому вигляді вони в жодних прикладах і реальних серйозних висловлюваннях не зустрічаються. Тому наше завдання полягає в тому, щоб навчитися бачити під літерами $a$ і $b$ набагато складніші конструкції, наприклад, логарифми, коріння, синуси тощо. Навчитися бачити це можна лише за допомогою постійної практики. Саме тому вирішувати раціональні дроби необхідно.

Друга, цілком очевидна формула - це розкладання квадратного тричлена на множники:

$((x)_(1))$; $((x)_(2))$ - коріння.

З теоретичною частиною ми розібралися. Але як вирішувати реальні раціональні дроби, що розглядаються у 8 класі? Зараз ми й потренуємось.

Завдання №1

\[\frac(27((a)^(3))-64((b)^(3)))(((b)^(3))-4):\frac(9((a)^ (2))+12ab+16((b)^(2)))(((b)^(2))+4b+4)\]

Спробуємо застосувати вищеописані формули до вирішення раціональних дробів. Насамперед, хочу пояснити, навіщо взагалі потрібне розкладання на множники. Справа в тому, що при першому погляді на першу частину завдання хочеться скоротити куб з квадратом, але робити цього категорично не можна, тому що вони складаються в чисельнику і в знаменнику, але в жодному разі не множниками.

Загалом, що таке скорочення? Скорочення — використання основного правила роботи з такими висловлюваннями. Основна властивість дробу полягає в тому, що ми можемо чисельник і знаменник можемо помножити на те саме число, відмінне від «нуля». В даному випадку, коли ми скорочуємо, то, навпаки, ділимо на те саме число, відмінне від «нуля». Однак ми повинні всі складові, що стоять у знаменнику, поділити на те саме число. Робити так не можна. І скорочувати чисельник із знаменником ми маємо право лише тоді, коли обидва вони розкладені на множники. Давайте це зробимо.

Тепер необхідно подивитися, скільки доданків знаходиться в тому чи іншому елементі, відповідно до цього дізнатися, яку формулу необхідно використати.

Перетворимо кожен вираз у точний куб:

Перепишемо чисельник:

\[((\left(3a \right))^(3))-((\left(4b \right))^(3))=\left(3a-4b \right)\left(((\left (3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2)) \right)\]

Погляньмо на знаменник. Розкладемо його за формулою різниці квадратів:

\[((b)^(2))-4=((b)^(2))-((2)^(2))=\left(b-2 \right)\left(b+2 \) right)\]

Тепер подивимося на другу частину виразу:

Чисельник:

Залишилося розібратися зі знаменником:

\[((b)^(2))+2\cdot 2b+((2)^(2))=((\left(b+2 \right))^(2))\]

Давайте перепишемо всю конструкцію з урахуванням перелічених вище фактів:

\[\frac(\left(3a-4b \right)\left(((\left(3a \right)))^(2))+3a\cdot 4b+((\left(4b \right))^(2) )) \right))(\left(b-2 \right)\left(b+2 \right))\cdot \frac(((\left(b+2 \right))^(2)))( ((\left(3a \right))^(2))+3a\cdot 4b+((\left(4b \right))^(2)))=\]

\[=\frac(\left(3a-4b \right)\left(b+2 \right))(\left(b-2 \right))\]

Нюанси множення раціональних дробів

Ключовий висновок із цих побудов наступний:

Не кожен многочлен розкладається на множники.
Навіть якщо він і розкладається, необхідно уважно дивитися, за якою формулою скороченого множення.

Для цього, по-перше, потрібно оцінити, скільки всього доданків (якщо їх два, то все, що ми можемо зробити, це розкласти їх або за сумою різниці квадратів, або за сумою або різницею кубів; а якщо їх три, то це , Однозначно, або квадрат суми, або квадрат різниці). Дуже часто буває так, що чисельник, чи знаменник взагалі вимагає розкладання на множники, може бути лінійним, чи дискримінант його буде негативним.

Завдання № 2

\[\frac(3-6x)(2((x)^(2))+4x+8)\cdot \frac(2x+1)(((x)^(2))+4-4x)\ cdot \frac(8-((x)^(3)))(4((x)^(2))-1)\]

Загалом схема вирішення цього завдання нічим не відрізняється від попередньої — просто дій буде більше, і вони стануть різноманітнішими.

Почнемо з першого дробу: подивимося на його чисельник і зробимо можливі перетворення:

Тепер подивимося на знаменник:

З другим дробом: у чисельнику взагалі нічого не можна зробити, тому що це лінійне вираження, і винести з нього якийсь множник не можна. Подивимося на знаменник:

\[((x)^(2))-4x+4=((x)^(2))-2\cdot 2x+((2)^(2))=((\left(x-2 \right) ))^(2))\]

Ідемо до третього дробу. Чисельник:

Розберемося зі знаменником останнього дробу:

Перепишемо вираз з урахуванням вищеописаних фактів:

\[\frac(3\left(1-2x \right))(2\left(((x)^(2))+2x+4 \right))\cdot \frac(2x+1)(((( \left(x-2 \right))^(2)))\cdot \frac(\left(2-x \right)\left(((2)^(2))+2x+((x)^( 2)) \right))(\left(2x-1 \right)\left(2x+1 \right))=\]

\[=\frac(-3)(2\left(2-x \right))=-\frac(3)(2\left(2-x \right))=\frac(3)(2\left (x-2 \right))\]

Нюанси рішення

Як бачите, далеко не все і не завжди впирається у формули скороченого множення — іноді просто достатньо винести за дужки константу чи змінну. Однак буває і зворотна ситуація, коли доданків настільки багато, або вони так побудовані, що формули скороченого множення до них взагалі неможливо. У цьому випадку до нас на допомогу приходить універсальний інструмент, а саме метод угруповання. Саме це ми зараз і застосуємо у наступному завданні.

Завдання №3

\[\frac(((a)^(2))+ab)(5a-((a)^(2))+((b)^(2))-5b)\cdot \frac(((a )^(2))-((b)^(2))+25-10a)(((a)^(2))-((b)^(2)))\]

Розберемо першу частину:

\[((a)^(2))+ab=a\left(a+b \right)\]

\[=5\left(a-b \right)-\left(a-b \right)\left(a+b \right)=\left(a-b \right)\left(5-1\left(a+b \right) ) \right)=\]

\[=\left(a-b \right)\left(5-a-b \right)\]

Давайте перепишемо вихідний вираз:

\[\frac(a\left(a+b \right))(\left(a-b \right)\left(5-a-b \right))\cdot \frac(((a)^(2))-( (b)^(2))+25-10a)(((a)^(2))-((b)^(2)))\]

Тепер розберемося з другою дужкою:

\[((a)^(2))-((b)^(2))+25-10a=((a)^(2))-10a+25-((b)^(2))= \left(((a)^(2))-2\cdot 5a+((5)^(2)) \right)-((b)^(2))=\]

\[=((\left(a-5 \right))^(2))-((b)^(2))=\left(a-5-b \right)\left(a-5+b \right)\]

Оскільки два елементи не вдалося згрупувати, ми згрупували три. Залишилося розібратися лише зі знаменником останнього дробу:

\[((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right)\]

Тепер перепишемо всю нашу конструкцію:

\[\frac(a\left(a+b \right))(\left(a-b \right)\left(5-a-b \right))\cdot \frac(\left(a-5-b \right) \left(a-5+b \right))(\left(a-b \right)\left(a+b \right))=\frac(a\left(b-a+5 \right))(((( \left(a-b \right))^(2)))\]

Завдання вирішене, і більше нічого спростити тут не можна.

Нюанси рішення

З угрупованням ми розібралися і отримали ще один дуже потужний інструмент, який розширює можливості розкладання на множники. Але проблема в тому, що в реальному житті нам ніхто не даватиме таких рафінованих прикладів, де є кілька дробів, у яких потрібно лише розкласти на множник чисельник і знаменник, а потім по можливості їх скоротити. Реальні висловлювання будуть набагато складнішими.

Швидше за все, крім множення і розподілу там будуть віднімання і додавання, всілякі дужки - взагалі, доведеться враховувати порядок дій. Але найстрашніше, що з відніманні й додаванні дробів із різними знаменниками їх доведеться приводити одного спільного. Для цього кожен із них потрібно буде розкладати на множники, а потім перетворювати ці дроби: наводити подібні та багато іншого. Як це зробити правильно, швидко, і при цьому отримати правильну відповідь? Саме про це ми поговоримо зараз на прикладі наступної конструкції.

Завдання № 4

\[\left(((x)^(2))+\frac(27)(x) \right)\cdot \left(\frac(1)(x+3)+\frac(1)(((( x)^(2))-3x+9) \right)\]

Давайте випишемо перший дріб і спробуємо розібратися з нею окремо:

\[((x)^(2))+\frac(27)(x)=\frac(((x)^(2)))(1)+\frac(27)(x)=\frac( ((x)^(3)))(x)+\frac(27)(x)=\frac(((x)^(3))+27)(x)=\frac(((x)^ (3))+((3)^(3)))(x)=\]

\[=\frac(\left(x+3 \right)\left(((x)^(2))-3x+9 \right))(x)\]

Переходимо до другої. Відразу порахуємо дискримінант знаменника:

Він на множники не розкладається, тому запишемо таке:

\[\frac(1)(x+3)+\frac(1)(((x)^(2))-3x+9)=\frac(((x)^(2))-3x+9 +x+3)(\left(x+3 \right)\left(((x)^(2))-3x+9 \right))=\]

\[=\frac(((x)^(2))-2x+12)(\left(x+3 \right)\left(((x)^(2))-3x+9 \right)) \]

Чисельник випишемо окремо:

\[((x)^(2))-2x+12=0\]

Отже, цей багаточлен на множники не розкладається.

Максимум, що ми могли зробити та розкласти, ми вже зробили.

Разом переписуємо нашу вихідну конструкцію та отримуємо:

\[\frac(\left(x+3 \right)\left(((x)^(2))-3x+9 \right))(x)\cdot \frac(((x)^(2) )-2x+12)(\left(x+3 \right)\left(((x)^(2))-3x+9 \right))=\frac(((x)^(2))- 2x+12)(x)\]

Все, завдання вирішено.

Якщо чесно, це було не таке вже й складне завдання: там все легко розкладалося на множники, швидко наводилися подібні доданки, і все гарно скорочувалося. Тому тепер давайте спробуємо вирішити завдання серйозніше.

Завдання № 5

\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \right)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \right)\]

Спочатку давайте розберемося з першою дужкою. З самого початку розкладемо на множники знаменник другого дробу окремо:

\[((x)^(3))-8=((x)^(3))-((2)^(3))=\left(x-2 \right)\left(((x) ^(2))+2x+4 \right)\]

\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3))-8 )-\frac(1)(((x)^(2)))=\]

\[=\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\left(x-2 \right)\ left(((x)^(2))+2x+4 \right))-\frac(1)(x-2)=\]

\[=\frac(x\left(x-2 \right)+((x)^(2))+8-\left(((x)^(2))+2x+4 \right))( \left(x-2 \right)\left(((x)^(2))+2x+4 \right))=\]

\[=\frac(((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))=\]

\[=\frac(((x)^(2))-4x+4)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right)) =\frac(((\left(x-2 \right))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right ))=\frac(x-2)(((x)^(2))+2x+4)\]

Тепер попрацюємо з другим дробом:

\[\frac(((x)^(2)))(((x)^(2))-4)-\frac(2)(2-x)=\frac(((x)^(2) )))(\left(x-2 \right)\left(x+2 \right))-\frac(2)(2-x)=\frac(((x)^(2))+2\ left(x-2 \right))(\left(x-2 \right)\left(x+2 \right))=\]

\[=\frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right))\]

Повертаємося до нашої вихідної конструкції та записуємо:

\[\frac(x-2)((((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2) \right)\left(x+2 \right))=\frac(1)(x+2)\]

Ключові моменти

Ще раз ключові факти сьогоднішнього відеоуроку:

Необхідно знати «назубок» формули скороченого множення — і не просто знати, а вміти бачити в тих виразах, які зустрічатимуться вам у реальних завданнях. Допомогти нам у цьому може чудове правило: якщо доданків два, то це або різниця квадратів, або різниця чи сума кубів; якщо три — це може бути лише квадрат суми чи різниці.
Якщо якась конструкція не розкладається за допомогою формул скороченого множення, то нам на допомогу приходить або стандартна формула розкладання тричленів на множники або метод угруповання.
Якщо щось не виходить, уважно подивіться на вихідний вираз — а чи взагалі потрібні якісь перетворення з ним. Можливо, досить просто винести множник за дужку, а це дуже часто буває просто константа.
У складних висловлюваннях, де потрібно виконати кілька дій поспіль, не забувайте приводити до спільного знаменника, і лише після цього, коли всі дроби приведені до нього, обов'язково наведіть подібне до нового чисельника, а потім новий чисельник ще раз розкладіть на множники — можливо, що скоротиться.

Ось і все, що я хотів вам розповісти сьогодні про раціональні дроби. Якщо щось незрозуміло, на сайті ще купа відеоуроків, а також купа завдань для самостійного вирішення. Тож залишайтеся з нами!

Будь-який дробовий вираз (п. 48) можна записати у вигляді , де Р і Q - раціональні вирази, причому Q обов'язково містить змінні. Такий дріб - називають раціональним дробом.

Приклади раціональних дробів:

Основна властивість дробу виражається тотожністю справедливою за умов тут - цілий раціональний вираз. Це означає, що чисельник і знаменник раціонального дробу можна помножити чи розділити одне й те відмінне від нуля число, одночлен чи многочлен.

Наприклад, властивість дробу може бути використана для зміни знаків членів дробу. Якщо чисельник та знаменник дробу - помножити на -1, отримаємо Таким чином, значення дробу не зміниться, якщо одночасно змінити знаки у чисельника та знаменника. Якщо ж змінити знак лише у чисельника чи тільки у знаменника, то й дріб змінить свої знак:

Наприклад,

60. Скорочення раціональних дробів.

Скоротити дріб - це означає розділити чисельник та знаменник дробу на загальний множник. Можливість такого скорочення обумовлена основною властивістю дробу.

Щоб скоротити раціональну дріб, потрібно чисельник і знаменник розкласти на множники. Якщо виявиться, що чисельник та знаменник мають спільні множники, то дріб можна скоротити. Якщо загальних множників немає, перетворення дробу у вигляді скорочення неможливо.

приклад. Скоротити дріб

Рішення. Маємо

Скорочення дробу виконано за умови.

61. Приведення раціональних дробів до спільного знаменника.

Спільним знаменником кількох раціональних дробів називається цілий раціональний вираз, який поділяється на знаменник кожного дробу (див. п. 54).

Наприклад, загальним знаменником дробів і служить многочлен оскільки він ділиться і на і багаточлен і многочлен і многочлен тощо. буд. Зазвичай беруть такий спільний знаменник, що будь-який інший спільний знаменник ділиться на Еібранний. Такий найпростіший знаменник називають іноді найменшим спільним знаменником.

У розглянутому вище прикладі загальний знаменник дорівнює Маємо

Приведення даних дробів до спільного знаменника досягнуто шляхом множення чисельника та знаменника першого дробу на 2. а чисельника та знаменника другого дробу на Багаточлени називаються додатковими множниками відповідно для першого та другого дробу. Додатковий множник для даного дробу дорівнює частці від поділу спільного знаменника на знаменник даного дробу.

Щоб кілька раціональних дробів привести до спільного знаменника, потрібно:

1) розкласти знаменник кожного дробу на множники;

2) скласти спільний знаменник, включивши в нього як співмножники всі множники отриманих у п. 1) розкладів; якщо деякий множник є у кількох розкладаннях, він береться з показником ступеня, рівним найбільшому з наявних;

3) знайде додаткові множники для кожного з дробів (для цього спільний знаменник ділять на знаменник дробу);

4) домноживши чисельник і знаменник кожного дробу на додатковий множник, привести дроб до загального знаменника.

приклад. Привести до спільного знаменника дробу

Рішення. Розкладемо знаменники на множники:

До загального знаменника треба включити такі множники: і найменше загальне кратне чисел 12, 18, 24, тобто . Отже, спільний знаменник має вигляд

Додаткові множники: для першого дробу для другого для третього Значить отримуємо:

62. Додавання та віднімання раціональних дробів.

Сума двох (і взагалі будь-якого кінцевого числа) раціональних дробів з однаковими знаменниками тотожно дорівнює дробу з тим же знаменником і з чисельником, рівним сумі чисельників дробів, що складаються:

Аналогічно справа у разі віднімання дробів з однаковими знаменниками:

Приклад 1. Спростити вираз

Рішення.

Для складання чи віднімання раціональних дробів з різними знаменниками потрібно передусім привести дроби до спільного знаменника, та був виконати операції над отриманими дробами з однаковими знаменниками.

Приклад 2. Спростити вираз

Рішення. Маємо

63. Множення та розподіл раціональних дробів.

Добуток двох (і взагалі будь-якого кінцевого числа) раціональних дробів тотожно дорівнює дробу, чисельник якого дорівнює добутку чисельників, а знаменник - добутку знаменників дробів, що перемножуються:

Приватне від поділу двох раціональних дробів тотожно дорівнює дробу, чисельник якого дорівнює добутку чисельника першого дробу на знаменник другого дробу, а знаменник - добутку внаменника першого дробу на чисельник другого дробу:

Сформульовані правила множення та поділу поширюються і на випадок множення або поділу на багаточлен: достатньо записати цей багаточлен у вигляді дробу зі знаменником 1.

Враховуючи можливість скорочення раціонального дробу, отриманого в результаті множення або поділу раціональних дробів, зазвичай прагнуть до виконання цих операцій розкласти на множники чисельники та знаменники вихідних дробів.

Приклад 1. Виконати множення

Рішення. Маємо

Використовуючи правило множення дробів, отримуємо:

Приклад 2. Виконати поділ

Рішення. Маємо

Використовуючи правило розподілу, отримуємо:

64. Зведення раціонального дробу на цілий ступінь.

Щоб звести раціональний дріб - в натуральний ступінь, потрібно звести в цей ступінь окремий чисельник і знаменник дробу; перший вираз – чисельник, а другий вираз – знаменник результату:

Приклад 1. Перетворити на дріб ступінь 3.

Рішення Рішення.

При зведенні дробу в цілий негативний ступінь використовується тотожність справедлива при всіх змінних значеннях, при яких .

Приклад 2. Перетворити на дріб вираз

65. Перетворення раціональних виразів.

Перетворення будь-якого раціонального виразу зводиться до додавання, віднімання, множення та поділу раціональних дробів, а також до зведення дробу в натуральний ступінь. Будь-який раціональний вираз можна перетворити на дріб, чисельник і знаменник якої - цілі раціональні вирази; у цьому, зазвичай, полягає мета тотожних перетворень раціональних виразів.

приклад. Спростити вираз

66. Найпростіші перетворення арифметичних коренів (радикалів).

При перетворенні арифметичних корій використовуються їх властивості (див. п. 35).

Розглянемо кілька прикладів застосування властивостей арифметичних коренів для найпростіших перетворень радикалів. При цьому всі змінні вважатимемо такими, що приймають тільки невід'ємні значення.

Приклад 1. Вийняти корінь із твору

Рішення. Застосувавши властивість 1°, отримаємо:

Приклад 2. Винести множник із-під знака кореня

Рішення.

Таке перетворення називається винесенням множника з-під знаку кореня. Мета перетворення - спростити підкорене вираз.

Приклад 3. Спростити.

Рішення. За якістю 3° маємо Зазвичай намагаються підкорене вираз спростити, навіщо виносять множники за знак корію. Маємо

Приклад 4. Спростити

Рішення. Перетворимо вираз, внісши множник під знак кореня: За властивістю 4° маємо

Приклад 5. Спростити

Рішення. За властивістю 5° ми маємо право показник кореня та показник ступеня підкореного виразу розділити на те саме натуральне число. Якщо в аналізованому прикладі розділити зазначені показники на 3, то отримаємо .

Приклад 6. Спростити вирази:

Рішення, а) За властивістю 1° отримуємо, що для перемноження коренів однієї й тієї ж ступеня достатньо перемножити підкорені вирази та з отриманого результату витягти корінь того ж ступеня. Значить,

б) Насамперед ми маємо привести радикали до одного показника. Відповідно до властивості 5° ми можемо показник кореня показник ступеня підкореного виразу помножити на те саме натуральне число. Тому Далі маємо тепер в отриманому результаті розділивши показники кореня і ступеня підкореного виразу На 3 отримаємо .

У цьому уроці розглядається множення та розподіл раціональних чисел.

Зміст уроку

Збільшення раціональних чисел

Правила множення цілих чисел справедливі й у раціональних чисел. Іншими словами, щоб множити раціональні числа, потрібно вміти

Також необхідно знати основні закони множення, такі як: переміщувальний закон множення, сполучний закон множення, розподільчий закон множення та множення на нуль.

приклад 1.Знайти значення виразу

Це множення раціональних чисел із різними знаками. Щоб перемножити раціональні числа з різними знаками, потрібно перемножити їх модулі і перед відповіддю поставити мінус.

Щоб добре побачити, що ми маємо справу з числами, у яких різні знаки, заключимо кожне раціональне число у дужки разом зі своїми знаками.

Модуль числа дорівнює, а модуль числа дорівнює. Перемноживши отримані модулі як позитивні дроби, ми отримали відповідь, але перед відповіддю поставили мінус, як від нас вимагало правило. Щоб забезпечити цей мінус перед відповіддю, множення модулів виконувалося в дужках, перед якими і поставлений мінус.

Коротке рішення виглядає так:

приклад 2.Знайти значення виразу

приклад 3.Знайти значення виразу

Це множення негативних раціональних чисел. Щоб перемножити негативні раціональні числа, потрібно перемножити їх модулі та перед отриманою відповіддю поставити плюс

Рішення для цього прикладу можна записати коротше:

приклад 4.Знайти значення виразу

Рішення для цього прикладу можна записати коротше:

Приклад 5.Знайти значення виразу

Це множення раціональних чисел із різними знаками. Перемножимо модулі цих чисел і перед отриманою відповіддю поставимо мінус

Коротке рішення виглядатиме значно простіше:

Приклад 6.Знайти значення виразу

Переведемо змішане число в неправильний дріб. Решту перепишемо, як є

Отримали множення раціональних чисел із різними знаками. Перемножити модулі цих чисел і перед отриманою відповіддю поставимо мінус. Запис із модулями можна пропустити, щоб не захаращувати вираз

Рішення для цього прикладу можна записати коротше

Приклад 7.Знайти значення виразу

Спочатку у відповіді вийшов неправильний дріб, але ми виділили в ньому цілу частину. Зверніть увагу, що цілу частину було виділено від модуля дробу . Змішане число, що вийшло, було укладено в дужки, перед якими поставлений мінус. Це зроблено у тому, щоб виконувалася вимога правила. А правило вимагало, щоб перед отриманим відповіддю стояв мінус.

Рішення для цього прикладу можна записати коротше:

Приклад 8.Знайти значення виразу

Спочатку перемножимо і отримане число перемножимо з числом 5, що залишилося. Запис з модулями пропустимо, щоб не захаращувати вираз.

Відповідь:значення виразу −2.

Приклад 9.Знайти значення виразу:

Перекладемо змішані числа в неправильні дроби:

Набули множення негативних раціональних чисел. Перемножити модулі цих чисел і перед отриманою відповіддю поставимо плюс. Запис із модулями можна пропустити, щоб не захаращувати вираз

приклад 10.Знайти значення виразу

Вираз складається з кількох співмножників. Відповідно до сполучного закону множення, якщо вираз складається з кількох співмножників, то твір не залежатиме від порядку дій. Це дозволяє нам обчислити цей вираз у будь-якому порядку.

Не будемо винаходити велосипед, а обчислимо цей вираз зліва направо в порядку прямування співмножників. Запис із модулями пропустимо, щоб не захаращувати вираз

Третя дія:

Четверта дія:

Відповідь:значення виразу дорівнює

Приклад 11.Знайти значення виразу

Згадуємо закон множення на нуль. Цей закон свідчить, що добуток дорівнює нулю, якщо хоча б один із співмножників дорівнює нулю.

У нашому прикладі один із співмножників дорівнює нулю, тому не втрачаючи часу відповідаємо, що значення виразу дорівнює нулю:

приклад 12.Знайти значення виразу

Добуток дорівнює нулю, якщо хоча б один із співмножників дорівнює нулю.

У нашому прикладі один із співмножників дорівнює нулю, тому не втрачаючи часу відповідаємо, що значення виразу одно нулю:

приклад 13.Знайти значення виразу

Можна скористатися порядком дій і спочатку обчислити вираз у дужках і отриману відповідь перемножити з дробом.

Ще можна скористатися розподільчим законом множення - помножити кожне доданок суми на дріб та отримані результати скласти. Цим способом і скористаємось.

Відповідно до порядку дій, якщо у виразі є додавання і множення, то в першу чергу потрібно виконувати множення. Тому в новому виразі візьмемо в дужки ті параметри, які повинні бути перемножені. Так ми добре побачимо, які дії виконати раніше, а які пізніше:

Третя дія:

Відповідь:значення виразу одно

Рішення для цього прикладу можна записати значно коротше. Виглядатиме воно наступним чином:

Видно, що цей приклад можна було вирішити навіть у думці. Тому слід розвивати у собі навичку аналізу висловлювання на початок його рішення. Цілком ймовірно, що його можна вирішити в умі і заощадити багато часу та нервів. А на контрольних та іспитах, як відомо, час дуже дорого коштує.

приклад 14.Знайти значення виразу -4,2 × 3,2

Зверніть увагу, як множилися модулі раціональних чисел. У разі, щоб перемножити модулі раціональних чисел, знадобилося .

приклад 15.Знайти значення виразу -0,15 × 4

Зверніть увагу, як множилися модулі раціональних чисел. У разі, щоб перемножити модулі раціональних чисел, знадобилося зуміти .

Приклад 16Знайти значення виразу -4,2 × (-7,5)

Це множення негативних раціональних чисел. Перемножимо модулі цих чисел і перед отриманою відповіддю поставимо плюс

Розподіл раціональних чисел

Правила поділу цілих чисел справедливі й у раціональних чисел. Іншими словами, щоб вміти поділяти раціональні числа, потрібно вміти

У іншому застосовуються самі методи поділу звичайних і десяткових дробів. Щоб розділити звичайний дріб на інший дріб, потрібно перший дріб помножити на дріб, зворотний другий.

А щоб розділити десятковий дріб на інший десятковий дріб, потрібно в діленому і в дільнику перенести кому вправо на стільки цифр, скільки їх після коми в дільнику, потім виконати поділ, як на звичайне число.

приклад 1.Знайти значення виразу:

Це розподіл раціональних чисел із різними знаками. Щоб обчислити такий вираз, потрібно перший дріб помножити на дріб, зворотний другий.

Отже, помножимо перший дріб на другий дріб.

Отримали множення раціональних чисел із різними знаками. А як обчислювати такі вирази, ми вже знаємо. Для цього потрібно перемножити модулі цих раціональних чисел та перед отриманою відповіддю поставити мінус.

Дорішаємо цей приклад до кінця. Запис із модулями можна пропустити, щоб не захаращувати вираз

Таким чином, значення виразу дорівнює

Докладне рішення виглядає так:

Коротке рішення виглядатиме так:

приклад 2.Знайти значення виразу

Це розподіл раціональних чисел із різними знаками. Щоб обчислити цей вираз, потрібно перший дріб помножити на дріб, зворотний другий.

Зворотний для другого дробу це дріб. На неї і помножимо перший дріб:

Коротке рішення виглядатиме так:

приклад 3.Знайти значення виразу

Це розподіл негативних раціональних чисел. Щоб обчислити цей вираз, знову ж таки потрібно перший дріб помножити на дріб зворотний другий.

Зворотний для другого дробу це дріб. На неї і помножимо перший дріб:

Набули множення негативних раціональних чисел. Як обчислюється такий вираз ми вже знаємо. Потрібно перемножити модулі раціональних чисел та перед отриманою відповіддю поставити плюс.

Дорішаємо цей приклад до кінця. Запис із модулями можна пропустити, щоб не захаращувати вираз:

приклад 4.Знайти значення виразу

Щоб обчислити цей вираз, потрібно перше число −3 помножити на дріб, зворотний до дробу .

Зворотний для дробу це дріб. На неї і помножимо перше число -3

Приклад 6.Знайти значення виразу

Щоб обчислити цей вираз, потрібно перший дріб помножити на число, протилежне числу 4.

Зворотне для числа 4 це дріб. На неї і помножимо перший дріб

Приклад 5.Знайти значення виразу

Щоб обчислити цей вираз, потрібно перший дроб помножити на число, обернене до −3

Зворотний для числа −3 це дріб. На неї і помножимо перший дріб:

Приклад 6.Знайти значення вираз −14,4: 1,8

Це розподіл раціональних чисел із різними знаками. Щоб обчислити цей вираз, потрібно модуль поділеного розділити на модуль дільника і перед отриманою відповіддю поставити мінус

Зверніть увагу, як модуль поділеного був поділений на модуль дільника. У цьому випадку, щоб зробити це правильно, знадобилося зуміти.

Якщо немає бажання возитися з десятковими дробами (а це буває часто), то ці, потім перевести ці змішані числа в неправильні дроби, а потім зайнятися безпосередньо розподілом.

Обчислимо попередній вираз -14,4: 1,8 цим способом. Переведемо десяткові дроби до змішаних цифр:

Тепер переведемо отримані змішані числа до неправильних дробів:

Тепер можна зайнятися безпосередньо розподілом, а саме розділити дріб на дріб. Для цього потрібно перший дріб помножити на дріб, зворотний другий:

Приклад 7.Знайти значення виразу

Переведемо десятковий дріб −2,06 у неправильний дріб, і помножимо цей дріб на дріб, зворотний другий:

Багатоповерхові дроби

Часто можна зустріти вираз, у якому розподіл дробів записано за допомогою дробової межі. Наприклад, вираз може бути записаний таким чином:

У чому різниця між висловлюваннями і ? Насправді різниці жодної. Ці два вирази несуть одне й те саме значення і між ними можна поставити знак рівності:

У першому випадку знак поділу є двокрапкою і вираз записано в один рядок. У другому випадку поділ дробів записано за допомогою дробової межі. В результаті виходить дріб, який у народі домовилися називати багатоповерховий.

При зустрічі з такими багатоповерховими виразами потрібно застосовувати ті ж правила поділу звичайних дробів. Перший дріб необхідно множити на дріб, зворотний другий.

Використовувати у рішенні подібні дроби вкрай незручно, тому можна записати їх у зрозумілому вигляді, використовуючи як знак розподілу не дробову межу, а двокрапку.

Наприклад, запишемо багатоповерховий дріб у зрозумілому вигляді. Для цього спочатку потрібно розібратися, де перший дріб і де другий, тому що зробити це правильно вдається не завжди. У багатоповерхових дробах є кілька дробових характеристик, які можуть заплутати. Головна дробова риса, яка відокремлює перший дріб від другого, зазвичай буває довшою за інші.

Після визначення головної дробової риси можна легко зрозуміти, де перший дріб і де другий:

приклад 2.

Знаходимо головну дробову межу (вона найдовша) і бачимо, що здійснюється розподіл цілого числа −3 на звичайний дріб

А якби ми помилково прийняли другу дробову межу за головну (ту, що коротше), то вийшло б, що ми ділимо дріб на ціле число 5. У цьому випадку, навіть якщо цей вираз обчислити правильно, завдання буде вирішено неправильно, оскільки ділимо в даному У разі є число −3, а дільником — дріб .

приклад 3.Запишемо у зрозумілому вигляді багатоповерховий дріб

Знаходимо головну дробову межу (вона найдовша) і бачимо, що здійснюється розподіл дробу на ціле число 2

А якби ми помилково прийняли першу дробову межу за головну (ту, що коротше), то вийшло б, що ми ділимо ціле число −5 на дріб. у разі є дріб , а дільником — ціле число 2.

Незважаючи на те, що багатоповерхові дроби незручні в роботі, ми стикаємося з ними дуже часто, особливо при вивченні вищої математики.

Природно, на переведення багатоповерхового дробу до зрозумілого вигляду йде додатковий час і місце. Тому можна скористатися швидшим методом. Даний метод зручний і на виході дозволяє отримати готовий вираз, в якому перший дріб вже помножений на дріб, зворотний другий.

Реалізується цей метод так:

Якщо дріб чотириповерховий, наприклад як , то цифру на першому поверсі піднімають на верхній поверх. А цифру, що знаходиться на другому поверсі, піднімають на третій поверх. Отримані цифри потрібно поєднати значками множення (×)

В результаті, минаючи проміжний запис ми отримуємо новий вираз, в якому перший дріб вже помножено на дріб, зворотний другий. Зручність та й годі!

Щоб не допускати помилок при використанні даного методу, можна керуватися таким правилом:

З першого на четвертий. З другого до третього.

У правилі йдеться про поверхи. Цифру з першого поверху слід піднімати на четвертий поверх. А цифру із другого поверху треба піднімати на третій поверх.

Спробуємо обчислити багатоповерховий дріб, користуючись вищенаведеним правилом.

Отже, цифру, що знаходиться на першому поверсі, піднімаємо на четвертий поверх, а цифру, що знаходиться на другому поверсі, піднімаємо на третій поверх.

В результаті, минаючи проміжний запис ми отримуємо новий вираз , в якому перший дріб вже помножено на дріб, зворотний другий. Далі можна скористатися наявними знаннями:

Спробуємо обчислити багатоповерховий дріб, користуючись новою схемою.

Тут є лише перший, другий та четвертий поверхи. Третій поверх відсутній. Але ми не відходимо від основної схеми: цифру з першого поверху піднімаємо на четвертий поверх. А оскільки третій поверх відсутній, то цифру, що знаходиться на другому поверсі, залишаємо, як є

В результаті, минаючи проміжний запис, ми отримали новий вираз , в якому перше число −3 вже помножено на дріб, зворотний другий. Далі можна скористатися наявними знаннями:

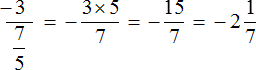
Спробуємо обчислити багатоповерховий дріб, користуючись новою схемою.

Тут є лише другий, третій та четвертий поверхи. Першого поверху немає. Оскільки перший поверх відсутній, підніматися на четвертий поверх нічому, але ми можемо підняти цифру з другого поверху на третій:

В результаті, минаючи проміжний запис ми отримали нове вираз, в якому перший дріб вже помножено на число, зворотне дільнику. Далі можна скористатися наявними знаннями:

Використання змінних

Якщо вираз складний і вам здається, що він заплутає вас у процесі розв'язання задачі, то частину виразу можна занести в змінну і далі працювати з цією змінною.

Математики часто так і роблять. Складне завдання розбивають більш легкі підзавдання і вирішують їх. Потім збирають вирішені підзавдання в єдине ціле. Це творчий процес і цього навчаються роками, наполегливо тренуючись.

Використання змінних виправдане при роботі з багатоповерховими дробами. Наприклад:

Знайти значення виразу

Отже, є дробовий вираз у чисельнику та в знаменнику якому дробові вирази. Іншими словами, перед нами знову багатоповерховий дріб, який ми так не любимо.

Вираз, що знаходиться в чисельнику, можна занести в змінну з будь-якою назвою, наприклад:

Але у математиці у разі змінним прийнято давати назву з великих латинських букв. Давайте не порушуватимемо цю традицію, і позначимо перший вираз через велику латинську букву A

А вираз, що знаходиться в знаменнику, можна позначити через велику латинську букву B

Тепер наш початковий вираз набуває вигляду. Тобто, ми зробили заміну числового виразу на буквене, попередньо внісши чисельник і знаменник змінні A і B.

Тепер ми можемо окремо обчислити значення змінної A і змінної B. Готові значення ми вставимо у вираз .

Знайдемо значення змінної A

Знайдемо значення змінної B

Тепер підставимо в головне вирази замість змінних A та B їх значення:

Ми отримали багатоповерховий дріб у якому можна скористатися схемою «з першого на четвертий, з другого на третій», тобто цифру, що знаходиться на першому поверсі, підняти на четвертий поверх, а цифру, що знаходиться на другому поверсі, підняти на третій поверх. Подальше обчислення не складе особливих труднощів:

Таким чином, значення виразу дорівнює -1.

Звичайно, ми розглянули найпростіший приклад, але нашою метою було дізнатися, як можна використовувати змінні для полегшення собі завдання, щоб звести до мінімуму помилки.

Зазначимо також, що рішення для цього прикладу можна записати не застосовуючи змінні. Виглядатиме воно як

Це рішення швидше і коротке і в даному випадку його доцільніше так і записати, але якщо вираз виявиться складним, що складається з декількох параметрів, дужок, коренів і ступенів, то бажано обчислювати його в кілька етапів, заносячи частину його виразів у змінні.

Сподобався урок?
Вступай у нашу нову групу Вконтакте та почні отримувати повідомлення про нові уроки