Рівняння нормалі до поверхні. Площина, що стосується поверхні

Рівняння нормальної площини

1.

4.

Дотична площина та нормаль до поверхні

Нехай дана деяка поверхня, A - фіксована точка поверхні і B - змінна точка поверхні,

Ненульовий вектор

Точка поверхні F (x, y, z) = 0 називається звичайною, якщо в цій точці

1. приватні похідні F"x, F"y, F"z безперервні;
2. (F"x)2+(F"y)2+(F"z)2≠0.

При порушенні хоча б однієї з цих умов точка поверхні називається особливою точкою поверхні .

Теорема 1.Якщо M (x 0 , y 0 , z 0 ) - Звичайна точка поверхні F (x , y , z) = 0 , то вектор

є нормальним до цієї поверхні в точці M (x 0, y 0, z 0).

Доведеннянаведено у книзі І.М. Петрушка, Л.А. Кузнєцова, В.І. Прохоренко, В.Ф. Сафонова `` Курс вищої математики: Інтегральне числення. Функції кількох змінних. Диференційне рівняння. М.: Вид-во МЕІ, 2002 (стор. 128).

Нормаллю до поверхнів деякій її точці називається пряма, напрямний вектор якої нормальний до поверхні в цій точці і яка проходить через цю точку.

Канонічні рівняння нормаліможна уявити у вигляді

Стосовною площиноюдо поверхні в деякій точці називається площина, яка проходить через цю точку перпендикулярно нормалі поверхні в цій точці.

З цього визначення випливає, що рівняння дотичної площинимає вигляд:

Якщо точка поверхні є особливою, то цій точці нормальний до поверхні вектор може не існувати, і, отже, поверхня може не мати нормалі і дотичної площини.

Геометричний зміст повного диференціалу функції двох змінних

Нехай функція z = f (x, y) диференційована в точці a (x0, y0). Її графіком є ​​поверхня

f (x, y) − z = 0.

Покладемо z 0 = f (x 0, y 0). Тоді точка A (x 0 y 0 z 0 ) належить поверхні.

Приватні похідні функції F (x, y, z) = f (x, y) − z суть

F " x = f " x , F " y = f " y , F " z = − 1

і в точці A (x 0, y 0, z 0)

1. вони безперервні;
2. F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0 .

Отже, A - звичайна точка поверхні F (x, y, z) і в цій точці існує дотична площина до поверхні. Відповідно до (3), рівняння дотичної площини має вигляд:

f " x ( x 0 , y 0 ) ( x - x 0 ) + f " y ( x 0 , y 0 ) ( y - y 0 ) - ( z - z 0 ) = 0 .

Вертикальне зміщення точки на дотичній площині під час переходу з точки a (x 0 , y 0 ) у довільну точку p (x , y) є B Q (рис. 2). Відповідне збільшення аплікати є

(z − z 0 ) = f " x (x 0 , y 0 ) (x − x 0 ) + f " y (x 0 , y 0 ) (y − y 0 )

Тут у правій частині стоїть диференціал d z функції z = f (x, y) у точці a (x0, x0). Отже,
d f (x 0, y 0). є збільшення аплікати точки площини дотичної до графіка функції f (x , y) в точці (x 0 , y 0 , z 0 = f (x 0 , y 0 )).

З визначення диференціала слід, що відстань між точкою P на графіку функції та точкою Q на дотичній площині є нескінченно мала більш високого порядку, ніж відстань від точки p до точки a .

1°. Рівняння дотичної площини та нормалі для випадку явного завдання поверхні.

Розглянемо один із геометричних додатків приватних похідних функції двох змінних. Нехай функція z = f (x;y)диференційована в точці (x 0; у 0)деякої області DÎ R 2. Розсічемо поверхню S ,зображуючу функцію z,площинами х = х 0і у = у 0(Рис. 11).

Площина х = x 0перетинає поверхню Sпо деякій лінії z 0 (y),рівняння якої виходить підстановкою у вираз вихідної функції z ==f (x;y)замість хчисла x0.Крапка M 0 (x 0;y 0,f (x 0;y 0))належить кривою z 0 (y).В силу функції, що диференціюється zу точці М 0функція z 0 (y)також є диференційованою в точці у = 0 .Отже, у цій точці в площині х = х 0до кривої z 0 (y)може бути проведена дотична l 1 .

Проводячи аналогічні міркування для перерізу у = у 0 ,побудуємо дотичну l 2до кривої z 0 (x)у точці х = x 0 -Прямі 1 1 і 1 2 визначають площину, яка називається дотичною площиноюдо поверхні Sу точці М0.

Складемо її рівняння. Так як площина проходить через точку Mo (x 0;y 0;z 0),то її рівняння може бути записано у вигляді

А (х - хо) + В (у - уо) + C (z - zo) = 0,

яке можна переписати так:

z -z 0 = A 1 (x - x 0) + B 1 (y - у 0) (1)

(розділивши рівняння на -С і позначивши ).

Знайдемо A 1та B 1 .

Рівняння дотичних 1 1 і 1 2 мають вигляд

відповідно.

Стосовна l 1лежить у площині a , отже, координати всіх точок l 1задовольняють рівняння (1). Цей факт можна записати у вигляді системи

Дозволяючи цю систему щодо B 1 отримаємо, що .Проводячи аналогічні міркування для дотичної l 3легко встановити, що .

Підставивши значення А 1і B 1 рівняння (1), отримуємо шукане рівняння дотичної площини:

Пряма, що проходить через точку М 0і перпендикулярна дотичній площині, побудованій у цій точці поверхні, називається її нормаллю.

Використовуючи умову перпендикулярності прямої та площини, легко отримати канонічні рівняння нормалі:

Зауваження.Формули дотичної площини та нормалі до поверхні отримані для звичайних, тобто не особливих точок поверхні. Крапка М 0поверхні називається особливою,якщо у цій точці всі приватні похідні дорівнюють нулю або хоча б одна з них не існує. Таких точок ми не розглядаємо.

приклад. Написати рівняння дотичної площини та нормалі до поверхні у її точці М(2; -1; 1).

Рішення. Знайдемо приватні похідні цієї функції та їх значення у точці М

Звідси, застосовуючи формули (2) і (3), матимемо: z-1=2(х-2)+2(у+1)або 2х+2у-z-1=0- рівняння дотичної площини та - Рівняння нормалі.

2 °. Рівняння дотичної площини та нормалі для випадку неявного завдання поверхні.

Якщо поверхня Sзадана рівнянням F (x; у;z)= 0, то рівняння (2) і (3), з огляду на те, що приватні похідні можуть бути знайдені як похідні неявної функції.

Дотичні площини відіграють велику роль у геометрії. Побудова дотичних площин у практичному відношенні має важливе значення, оскільки наявність їх дозволяє визначити напрямок нормалі до поверхні у точці дотику. Це завдання знаходить широке застосування інженерної практиці. До допомоги дотичних площин звертаються також побудови нарисів геометричних фігур, обмежених замкнутими поверхнями. У теоретичному плані площини, що стосуються поверхні, використовуються в диференціальній геометрії при вивченні властивостей поверхні в районі точки торкання.

Основні поняття та визначення

Площину, що стосується поверхні, слід розглядати як граничне положення сіючої площини (за аналогією з прямою, що стосується кривої, яка також визначається як граничне положення сіючої).

Площина, що стосується поверхні в заданій на поверхні точці, є безліч всіх прямих - дотичних, проведених до поверхні через задану точку.

У диференціальній геометрії доводиться, що психічні до поверхні, проведені у звичайній точці, компланарні (належать одній площині).

З'ясуємо, як проводиться пряма, що стосується поверхні. Дотична t до поверхні β в заданій на поверхні точці М (рис. 203) представляє граничне положення сіючої l j , що перетинає поверхню в двох точках (ММ 1 , ММ 2 , ..., ММ n), коли точки перетину збігаються (М ≡ М n , l n ≡ l M). Очевидно (M 1 , М 2 ..., М n ) ∈ g, так як g ⊂ β. Зі сказаного вище випливає таке визначення: дотичної до поверхні називається пряма, дотична до будь-якої кривої, що належить поверхні.

Так як площина визначається двома прямими, що перетинаються, то для завдання площини, дотичної до поверхні в заданій точці, достатньо провести через цю точку дві довільні лінії, що належать поверхні (бажано прості за формою), і до кожної з них побудувати дотичні в точці перетину цих ліній . Побудовані дотичні однозначно визначають дотичну площину. Наочне уявлення про проведення площини α, що стосується поверхні β в заданій точці М, дає рис. 204. На цьому малюнку показано також нормаль n до поверхні β.

Нормлю до поверхні в заданій точці називається пряма, перпендикулярна до дотичної площини і проходить через точку торкання.

Лінію перетину поверхні площиною, що проходить через нормаль, називають нормальним перерізом поверхні. Залежно від виду поверхні дотична площина може мати з поверхнею як одну, так і безліч точок (лінію). Лінія торкання може бути одночасно і лінією перетину поверхні з площиною.

Можливі також випадки, коли на поверхні є точки, на яких неможливо провести дотичну до поверхні; такі точки називають особливими. Як приклад особливих точок можна навести точки, що належать ребру повернення торсової поверхні, або точку перетину меридіана поверхні обертання з її віссю, якщо меридіан і вісь перетинаються не під прямим кутом.

Види торкання залежить від характеру кривизни поверхні.

Кривизна поверхні

Питання кривизни поверхні було досліджено французьким математиком Ф. Дюпеном (1784- 1873), який запропонував наочний спосіб зображення зміни кривизни нормальних перерізів поверхні.

Для цього в площині, що стосується до поверхні, що розглядається в точці М (рис. 205, 206), на дотичних до нормальних перерізів по обидва боки від даної точки відкладаються відрізки, рівні корінням квадратним з величин відповідних радіусів кривизни цих перерізів. Безліч точок - кінців відрізків задають криву, звану індикатриса Дюпена. Алгоритм побудови індикатриси Дюпена (рис. 205) можна записати:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(R l 1), = √(R l 2),..., = √(R l n)

де R – радіус кривизни.

(A 1 ∪ А 2 ∪ ... ∪ А n) - індикатриса Дюпена.

Якщо індикатриса Дюпена поверхні – еліпс, то точка М називається еліптичною, а поверхня – поверхнею з еліптичними точками(Рис. 206). У цьому випадку дотична площина має з поверхнею тільки одну загальну точку, а всі лінії, що належать поверхні і перетинаються в точці, розташовані по одну сторону від дотичної площини. Прикладом поверхонь з еліптичними точками можуть бути параболоїд обертання, еліпсоїд обертання, сфера (у цьому випадку індикатриса Дюпена - коло та ін.).

При проведенні дотичної площини до торсової поверхні площина буде торкатися цієї поверхні прямої утворює. Точки цієї прямої називаються параболічними, а поверхня - поверхнею з параболічними точками. Індикатриса Дюпена у разі - дві паралельні прямі (рис. 207*).

На рис. 208 показана поверхня, що складається з точок, в кото

* Крива другого порядку - парабола - за певних умов може розпадатися на дві дійсні паралельні прямі, дві уявні паралельні прямі, дві прямі, що збігаються. На рис. 207 ми маємо справу з двома дійсними паралельними прямими.

рих дотична площина перетинає поверхню. Така поверхня називається гіперболічної, А належні їй точки - гіперболічними точками. Індикатриса Дюпена в даному випадку – гіпербола.

Поверхня, всі точки якої є гіперболічними, має форму сідла (коса площина, однопорожнинний гіперболоїд, увігнуті поверхні обертання та ін.).

Одна поверхня може мати точки різних видів, наприклад, біля торсової поверхні (рис. 209) точка М еліптична; точка N – параболічна; точка К – гіперболічна.

У курсі диференціальної геометрії доводиться, що нормальні перерізи, у яких величини кривизни K j = 1/ R j (де R j радіус кривизни аналізованого перерізу) мають екстремальні значення, розташовані у двох взаємно перпендикулярних площинах.

Такі кривизни К1 = 1/R max. К 2 = 1/R min називаються головними, а значення Н = (К 1 + К 2)/2 і К = К 1 К 2 - відповідно середньої кривизною поверхні та повної (гаусової) кривизної поверхні в точці, що розглядається. Для еліптичних точок К > 0, гіперболічних К

Завдання площини дотичної до поверхні на епюрі Монжа

Нижче на конкретних прикладах покажемо побудова площини, що стосується поверхні з еліптичними (приклад 1), параболічними (приклад 2) і гіперболічними (приклад 3) точками.

ПРИКЛАД 1. Побудувати площину α, що стосується поверхні обертання β, з еліптичними точками. Розглянемо два варіанти розв'язання цього завдання, а) точка М ∈ β та б) точка М ∉ β

Варіант а (рис. 210).

Дотична площина визначається двома дотичними t 1 і t 2 проведеними в точці М до паралелі і меридіану поверхні β.

Проекції дотичної t 1 до паралелі поверхні h β будуть t" 1 ⊥ (S"M") і t" 1 || осі х. Горизонтальна проекція дотичної t" 2 до меридіана d поверхні β, що проходить через точку М, збігається з горизонтальною проекцією меридіана. Щоб знайти фронтальну проекцію дотичної t" 2 , меридіональну площину γ(γ ∋ М) шляхом обертання навколо осі поверхні β 1 , паралельне площині π 2 . У цьому випадку точка М → M 1 (М" 1 , М" 1). Проекція дотичної t" 2 rarr; t" 2 1 визначається (M" 1 S"). Якщо ми тепер повернемо площину 1 у початкове положення, то точка S" залишиться на місці (як належить осі обертання), а М" 1 → М" і фронтальна проекція дотичної t" 2 визначиться (M"S")

Дві перетинаються в точці М ∈ β дотичні t 1 і t 2 визначають площину α, що стосується поверхні β.

Варіант б (рис. 211)

Для побудови площини, що стосується поверхні, що проходить через точку, не належить поверхні, потрібно виходити з таких міркувань: через точку поза поверхнею, що складається з еліптичних точок, можна провести безліч площин, дотичних до поверхні. Огинає цих поверхонь буде деяка конічна поверхня. Тому, якщо немає додаткових вказівок, завдання має безліч рішень і в такому випадку зводиться до проведення конічної поверхні γ, що стосується до даної поверхні β.

На рис. 211 показано побудову конічної поверхні γ, що стосується сфери β. Будь-яка площина α, що стосується конічної поверхні γ, буде дотичною до поверхні β.

Для побудови проекцій поверхні з точок М" і М" проводимо дотичні до кіл h" і f" - проекціям сфери. Зазначаємо точки торкання 1 (1" та 1"), 2 (2" та 2"), 3 (3" і 3") та 4 (4" і 4"). Горизонтальна проекція кола - лінія торкання конічної поверхні та сфери спроектується в [ 1"2"] Для знаходження точок еліпса, в який це коло спроектується на фронтальну площину проекцій, скористаємося паралелями сфери.

На рис. 211 у такий спосіб визначено фронтальні проекції точок Е та F (Е" і F"). Маючи конічну поверхню γ, будуємо до неї дотичну площину. Характер і послідовність графіки

ких побудов, які необхідно для цього виконати, наведено в наступному прикладі.

ПРИКЛАД 2 Побудувати площину α, що стосується поверхні β з параболічними точками

Як у прикладі 1 розглянемо два варіанти розв'язання.а) точка N ∈ β; б) точка N ∉ β

Варіант а (рис 212).

Конічна поверхня відноситься до поверхонь з параболічними точками (див. рис. 207.) Площина, дотична до конічної поверхні, стосується її прямолінійної утворюючої. Для її побудови необхідно:

1) через дану точку N провести утворюючу SN (S"N" і S"N");

2) відзначити точку перетину утворюючої (SN) з напрямною d: (SN) ∩ d = А;

3) провіє і дотичну t до d в точці А.

Утворююча (SA) і перетинає її дотична t визначають площину α , що стосується конічної поверхні β в даній точці N *.

Для проведення площини α, що стосується конічної поверхні β і проходить через точку N, не належить

* Оскільки поверхня β складається з параболічних точок (крім вершини S), то дотична до неї площина буде мати спільну з нею не одну точку N, а пряму (SN).

спрагу заданої поверхні, необхідно:

1) через дану точку N і вершину S конічної поверхні β провести пряму а (а" і а");

2) визначити горизонтальний слід цієї прямої Н a ;

3) через Н a провести дотичні t" 1 і t" 2 кривої h 0β - горизонтальному сліду конічної поверхні;

4) точки дотику А (А" та А") і В (В" і В") з'єднати з вершиною конічної поверхні S (S" і S").

Прямі t 1 , (AS) і t 2 , (BS), що перетинаються, визначають шукані дотичні площини α 1 і α 2

ПРИКЛАД 3. Побудувати площину α, що стосується поверхні β з гіперболічними точками.

Крапка К (рис. 214) знаходиться на поверхні глобоїда (внутрішня поверхня кільця).

Для визначення положення щодо площини α необхідно:

1) провести через точку К паралель поверхні h(h", h");

2) через точку К" провести дотичну t" 1 (t" 1 ≡ h") ;

3) для визначення напрямків проекцій дотичної до меридіонального перерізу необхідно провести через точку К і вісь поверхні площину γ, горизонтальна проекція t" 2 збігається з h 0γ ; для побудови фронтальної проекції дотичної t" 2 попередньо переведемо площину γ шляхом обертання її навколо осі поверхні обертання у положення γ 1 || π 2 . У цьому випадку меридіональний переріз площиною γ поєднається з лівою нарисовою дугою фронтальної проекції - півколо g".

Точка До (К", К"), що належить кривій меридіонального перерізу, переміститься в положення K 1 (К" 1 , К" 1). Через К" 1 проводимо фронтальну проекцію дотичної t" 2 1 в суміщеному з площиною γ 1 || ? К" та S".

Дотичні t 1 і t 2 визначають потрібну дотичну площину α, яка перетинає поверхню β по кривій l .

ПРИКЛАД 4. Побудувати площину α, що стосується поверхні β у точці К. Точка К знаходиться на поверхні однопорожнинного гіперболоїду обертання (рис. 215).

Це завдання можна вирішити, дотримуючись алгоритму, використаного в попередньому прикладі, але враховуючи, що поверхня однопорожнинного гіперболоїда обертання є лінійчастою поверхнею, яка має два сімейства прямолінійних утворюючих, причому кожна з утворюють одного сімейства перетинає всі утворюють іншого сімейства (див. § 32, рис. 138). Через кожну точку цієї поверхні можна провести дві прямі - утворювальні, що перетинаються, які будуть одночасно дотичними до поверхні однопорожнинного гіперболоїда обертання.

Ці дотичні визначають дотичну площину, тобто площину, що стосується поверхні однопорожнинного гіперболоїда обертання, перетинає цю поверхню за двома прямими g 1 і g 2 . Для побудови проекцій цих прямих достатньо горизонтальної проекції точки До пронести дотичні t" 1 і t" 2 до горизон-

тальної проекції кола d" 2 - горла поверхні однопорожнинного гіперболоїда обертання; визначити точки 1" і 2 , в яких t" 1 і t" 2 перетинають одну іт напрямних поверхні d 1 . По 1" і 2" знаходимо 1" і 2", які спільно з К" визначають фронтальні проекції прямих шуканих.

Завантажити з Depositfiles

4. ТЕОРІЯ ПОВЕРХНІВ.

4.1 РІВНЯННЯ ПОВЕРХНОСТЕЙ.

Поверхня в тривимірному просторі може бути задана:

1) неявно: F ( x , y , z ) =0 (4.1)

2) явно: z = f ( x , y ) (4.2)

3) параметрично: (4.3)

або:
(4.3’)

де скалярні аргументи
іноді називають криволінійними координатами. Наприклад, сферу
зручно задавати у сферичних координатах:
.

4.2 ЩОДО ПЛОСКІСТЬ І НОРМАЛЬ ДО ПОВЕРХНІ.

Якщо лінія лежить на поверхні (4.1), то координати її точок задовольняють рівняння поверхні:

Диференціюючи це тотожність, отримаємо:

(4.4)

або
(4.4 ’ )

у кожній точці кривої на поверхні. Таким чином, вектор градієнта в неособливих точках поверхні (у яких функція (4.5) диференційована і
) перпендикулярний дотичних векторів до будь-яких ліній на поверхні, тобто може бути використаний як вектор нормалі для складання рівняння дотичної площини в точці М 0 (x 0 , y 0 , z 0 ) поверхні

(4.6)

і як напрямний вектор у рівнянні нормалі:

(4.7)

У разі явного (4.2) завдання поверхні рівняння дотичної площини та нормалі відповідно наберуть вигляду:

(4.8)

і
(4.9)

При параметричному поданні поверхні (4.3) вектори
лежать у дотичній площині та рівняння дотичної площини може бути записане у вигляді:

(4.10)

а як напрямний вектор нормалі може бути прийнято їх векторний твір:

і рівняння нормалі може бути записано у вигляді:

(4.11)

де
— значення параметрів відповідні точці М 0 .

Надалі ми обмежимося розглядом лише таких точок поверхні, де вектори

не рівні нулю та не паралельні.

Приклад 4.1 Скласти рівняння дотичної площини та нормалі у точці М 0 (1,1,2) до поверхні параболоїда обертання
.

Рішення: Так як рівняння параболоїда задано у явному вигляді, то згідно (4.8) та (4.9) потрібно знайти
у точці М 0 :

, А в точці М 0
. Тоді рівняння дотичної площини у точці М 0 набуде вигляду:

2(x -1)+2(y -1)-(z-2) = 0 або 2 x +2 y - z ‑ 2=0, а рівняння нормалі
.

Приклад 4.2 Скласти рівняння дотичної площини та нормалі у довільній точці гелікоїда
, .

Рішення. Тут ,

Рівняння дотичної площини:

або

Рівняння нормалі:

.

4.3 ПЕРША КВАДРАТИЧНА ФОРМА ПОВЕРХНІ.

Якщо поверхня задається рівнянням

то крива
на ній може бути задана рівнянням
(4.12)

Диференціал радіус-вектора
вздовж кривої, що відповідає зсуву з точки М 0 у прилеглу точку М, дорівнює

(4.13)

Так як
- Диференціал дуги кривої, що відповідає тому ж зсуву), то

(4.14)

де.

Вираз у правій частині (4.14) називається першою квадратичною формою поверхні і грає теоретично поверхонь величезну роль.

Інтегрую диференціалdsв межах від t 0 (відповідає точці М 0) до t (відповідає точці М), отримаємо довжину відповідного відрізка кривої

(4.15)

Знаючи першу квадратичну форму поверхні, можна знаходити не лише довжини, а й кути між кривими.

Якщо du , dv - Диференціали криволінійних координат, що відповідають нескінченно малому зміщенню по одній кривій, а
- Іншою, то з урахуванням (4.13):

(4.16)

За допомогою формули

(4.17)

перша квадратична форма дає можливість обчислити площу області
поверхні.

Приклад 4.3 На гелікоїді , знайти довжину гвинтової лінії
між двома точками.

Рішення. Оскільки на гвинтовій лінії
, то. Знайдемо в точці
першу квадратичну форму. Позначивши таv = t , отримаємо рівняння даної гвинтової лінії у вигляді. Квадратична форма:

= - Перша квадратична форма.

Тут. У формулі (4.15) у цьому випадку
та довжина дуги:

=

4.4 ДРУГА КВАДРАТИЧНА ФОРМА ПОВЕРХНІ.

Позначимо
‑ одиничний вектор нормалі до поверхні
:

(4.18) . (4.23)

Лінія лежить на поверхні називається лінією кривизни, якщо її напрям у кожній точці є головним напрямом.

4.6 ПОНЯТТЯ ПРО ГЕОДЕЗИЧНІ ЛІНІЇ НА ПОВЕРХНІ.

Визначення 4.1 . Крива на поверхні називається геодезичною, якщо її головна нормаль у кожній точці, де кривизна відмінна від нуля, збігається з нормаллю 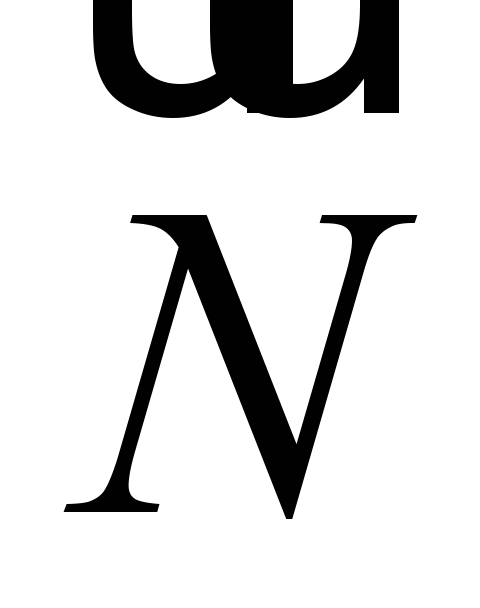до поверхні.

Через кожну точку поверхні в будь-якому напрямку проходить, і при цьому лише одна геодезична. На сфері, наприклад, геодезичними є великі кола.

Параметризація поверхні називається напівгеодезичною, якщо одне сімейство координатних ліній складається з геодезичних, а друге йому ортогонально. Наприклад, на сфері меридіани (геодезичні) та паралелі.

Геодезична на досить малому відрізку є найкоротшою серед усіх близьких до неї кривих, що з'єднують самі точки.

Нехай маємо поверхню, задану рівнянням виду

Введемо таке визначення.

Визначення 1. Пряма лінія називається дотичною до поверхні в деякій точці, якщо вона є

дотичної до будь-якої кривої, що лежить на поверхні і проходить через точку .

Так як через точку Р проходить нескінченна кількість різних кривих, що лежать на поверхні, то і дотичних до поверхні, що проходять через цю точку, буде, взагалі кажучи, безліч.

Введемо поняття про особливі та звичайні точки поверхні

Якщо у точці всі три похідні дорівнюють нулю або хоча б одна з цих похідних не існує, то точка М називається особливою точкою поверхні. Якщо в точці всі три похідні існують і безперервні, причому хоча одна з них відмінна від нуля, то точка М називається звичайною точкою поверхні.

Тепер ми можемо сформулювати таку теорему.

Теорема. Усі дотичні прямі до цієї поверхні (1) у її звичайній точці Р лежать у одній площині.

Доведення. Розглянемо на поверхні деяку лінію L (рис. 206), що проходить через цю точку Р поверхні. Нехай крива, що розглядається, задана параметричними рівняннями

Стосовна до кривої буде дотичною до поверхні. Рівняння цієї дотичної мають вигляд

Якщо вирази (2) підставити рівняння (1), це рівняння перетвориться на тотожність щодо t, оскільки крива (2) лежить на поверхні (1). Диференціюючи його по отримаємо

Проекції цього вектора залежать від координат точки Р; зауважимо, що оскільки точка Р звичайна, то ці проекції в точці Р одночасно не звертаються в нуль і тому

дотичний до кривої, що проходить через точку Р і лежить на поверхні. Проекції цього вектора обчислюються виходячи з рівнянь (2) при значенні параметра t, відповідному точці Р.

Обчислимо скалярний добуток векторів N і який дорівнює сумі творів однойменних проекцій:

На підставі рівності (3) вираз, що стоїть у правій частині, дорівнює нулю, отже,

З останньої рівності випливає, що вектор ЛГ та дотичний вектор до кривої (2) у точці Р перпендикулярні. Проведене міркування справедливо для будь-якої кривої (2), що проходить через точку Р і лежить на поверхні. Отже, кожна дотична до поверхні в точці Р перпендикулярна до одного й тому вектору N і тому всі ці дотичні лежать в одній площині, перпендикулярної до вектора ЛГ. Теорему доведено.

Визначення 2. Площина, в якій розташовані всі дотичні до ліній на поверхні, що проходять через дану її точку Р, називається дотичною площиною до поверхні в точці Р (рис. 207).

Зауважимо, що в спеціальних точках поверхні може не існувати дотичної поверхні. У таких точках дотичні прямі поверхні можуть не лежати в одній площині. Так, наприклад, вершина конічної поверхні є особливою точкою.

Щодо конічної поверхні в цій точці не лежать в одній площині (вони самі утворюють конічну поверхню).

Напишемо рівняння дотичної площини до поверхні (1) у звичайній точці. Так як ця площина перпендикулярна вектору (4), то, отже, її рівняння має вигляд

Якщо рівняння поверхні задано у формі або рівняння дотичної площини в цьому випадку набуде вигляду

Зауваження. Якщо у формулі (6) покладемо , то ця формула набуде вигляду

її права частина є повний диференціал функції. Отже, . Таким чином, повний диференціал функції двох змінних у точці, що відповідає прирощенням незалежних змінних х і у, дорівнює відповідному прирощенню аплікати дотичної площини до поверхні, яка є графіком даної функції.

Визначення 3. Пряма, проведена через точку поверхні (1) перпендикулярно до дотичної площини, називається нормаллю до поверхні (рис. 207).

Напишемо рівняння нормалі. Оскільки її напрямок збігається з напрямком вектора N, її рівняння матимуть вигляд