Практична робота: Перетворення графіків функцій. Похідна Геометричний зміст похідної
Похідної функції $y = f(x)$ в даній точці $х_0$ називають межу відношення збільшення функції до відповідного збільшення його аргументу за умови, що останнє прагне до нуля:
$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$
Диференціюванням називають операцію знаходження похідної.
Таблиця похідних деяких елементарних функцій
| Функція | Похідна |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^(n-1)$ |
| $(1)/(x)$ | $-(1)/(x^2)$ |
| $√x$ | $(1)/(2√x)$ |
| $e^x$ | $e^x$ |
| $lnx$ | $(1)/(x)$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $(1)/(cos^2x)$ |
| $ctgx$ | $-(1)/(sin^2x)$ |
Основні правила диференціювання
1. Похідна суми (різниці) дорівнює сумі (різниці) похідних
$(f(x) ± g(x))"= f"(x)±g"(x)$
Знайти похідну функції $f(x)=3x^5-cosx+(1)/(x)$
Похідна суми (різниці) дорівнює сумі (різниці) похідних.
$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$
2. Похідна твори
$(f(x) · g(x))"= f"(x) · g(x)+ f(x) · g(x)"$
Знайти похідну $f(x)=4x·cosx$
$f"(x)=(4x)"·cosx+4x·(cosx)”=4·cosx-4x·sinx$
3. Похідна приватного
$((f(x))/(g(x)))"=(f"(x)·g(x)-f(x)·g(x)")/(g^2(x)) $
Знайти похідну $f(x)=(5x^5)/(e^x)$
$f"(x)=((5x^5)"·e^x-5x^5·(e^x)")/((e^x)^2)=(25x^4·e^x- 5x^5·e^x)/((e^x)^2)$
4. Похідна складної функції дорівнює добутку похідної зовнішньої функції на похідну внутрішньої функції
$f(g(x))"=f"(g(x))·g"(x)$
$f"(x)=cos"(5x)·(5x)"=-sin(5x)·5= -5sin(5x)$
Фізичний зміст похідної
Якщо матеріальна точка рухається прямолінійно та її координата змінюється залежно від часу за законом $x(t)$, то миттєва швидкість цієї точки дорівнює похідної функції.
Крапка рухається по координатній прямій згідно із законом $x(t)= 1,5t^2-3t + 7$, де $x(t)$ - координата в момент часу $t$. У який момент часу швидкість точки дорівнюватиме $12$?
1. Швидкість – це похідна від $x(t)$, тому знайдемо похідну заданої функції
$v(t) = x"(t) = 1,5 · 2t -3 = 3t -3$
2. Щоб знайти, в який момент часу $t$ швидкість дорівнювала $12$, складемо і вирішимо рівняння:
Геометричний зміст похідної
Нагадаємо, що рівняння прямої, не паралельної до осей координат, можна записати у вигляді $y = kx + b$, де $k$ – кутовий коефіцієнт прямий. Коефіцієнт $k$ дорівнює тангенсу кута нахилу між прямим і позитивним напрямом осі $Ох$.
Похідна функції $f(x)$ у точці $х_0$ дорівнює кутовому коефіцієнту $k$ щодо графіка в даній точці:
Отже, можемо скласти загальну рівність:
$f"(x_0) = k = tgα$
На малюнку щодо функції $f(x)$ зростає, отже, коефіцієнт $k > 0$. Оскільки $k > 0$, то $f"(x_0) = tgα > 0$. Кут $α$ між дотичною і позитивним напрямком $Ох$ гострий.
На малюнку щодо функції $f(x)$ зменшується, отже, коефіцієнт $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На малюнку, що стосується функції $f(x)$ паралельна осі $Ох$, отже, коефіцієнт $k = 0$, отже, $f"(x_0) = tg α = 0$. Точка $x_0$, в якій $f "(x_0) = 0$, називається екстремумом.
На малюнку зображено графік функції $y=f(x)$ і дотичну до цього графіку, проведену в точці з абсцисою $x_0$. Знайдіть значення похідної функції $f(x)$ у точці $x_0$.
Щодо графіка зростає, отже, $f"(x_0) = tg α > 0$
Для того, щоб знайти $f"(x_0)$, знайдемо тангенс кута нахилу між дотичною та позитивним напрямком осі $Ох$. Для цього добудуємо дотичну до трикутника $АВС$.
Знайдемо тангенс кута $ВАС$. (Тангенсом гострого кута у прямокутному трикутнику називається відношення протилежного катета до прилеглого катета.)
$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$
$f"(x_0) = tg ВАС = 0,25 $
Відповідь: $0,25$
Похідна так само застосовується для знаходження проміжків зростання та зменшення функції:
Якщо $f"(x) > 0$ на проміжку, то функція $f(x)$ зростає у цьому проміжку.
Якщо $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На малюнку зображено графік функції $ y = f (x) $. Знайдіть серед точок $х_1,х_2,х_3…х_7$ ті точки, у яких похідна функції негативна.
У відповідь запишіть кількість даних.
У завданні №13 ЄДІ з математики базового рівня доведеться продемонструвати вміння та знання одного з понять поведінки функції: похідних у точці або швидкостей зростання чи спадання. Теорія до цього завдання буде додано трохи згодом, але це завадить нам докладно розібрати кілька типових варіантів.
Розбір типових варіантів завдань №14 ЄДІ з математики базового рівня
Варіант 14МБ1
На графіці зображено залежність температури від часу у процесі розігріву двигуна легкового автомобіля. На горизонтальній осі відзначено час у хвилинах, що минув з моменту запуску двигуна; на вертикальній осі – температура двигуна у градусах Цельсія.

Користуючись графіком, поставте у відповідність до кожного інтервалу часу характеристику процесу розігріву двигуна на цьому інтервалі.
У таблиці під кожною літерою вкажіть відповідний номер.
Алгоритм виконання:
- Вибрати інтервал часу, коли температура падала.
- Прикласти лінійку до 30°З визначити інтервал часу, у якому температура була нижче 30°С.
Рішення:
Виберемо інтервал часу, у якому температура падала. Ця ділянка видно не озброєним оком, вона починається о 8 хв від моменту запуску двигуна.
Докладемо лінійку до 30°З визначення інтервал часу, у якому температура була нижче 30°С.

Нижче за лінійку виявиться ділянка, що відповідає інтервалу часу 0 – 1 хв.
За допомогою олівця та лінійки знайдемо на якому інтервалі часу температура перебувала в межах від 40°С до 80°С.
Опустимо з точок, відповідних 40°З 80°З перпендикуляри на графік, та якщо з отриманих точок опустимо перпендикуляри на вісь часу.

Бачимо, що температурному інтервалу відповідає інтервал часу 3 – 6,5 хв. Тобто із наведених за умови 3 – 6 хв.
Методом виключення виберемо недостатній варіант відповіді.
Варіант 14МБ2
Рішення:
Проаналізуємо графік функції А. Якщо функція зростає, то похідна позитивна і навпаки. Похідна функції дорівнює нулю в точках екстремуму.
Спочатку функція А збільшується, тобто. похідна позитивна. Цьому відповідають графіки похідних 2 і 3. У точці максимуму функції x=-2, тобто в цій точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 3.
Спочатку функція Б зменшується, тобто. похідна негативна. Цьому відповідають графіки похідних 1 і 4. Точка максимуму функції x=-2, тобто в даній точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 4.
Спочатку функція зростає, тобто. похідна позитивна. Цьому відповідають графіки похідних 2 і 3. Точка максимуму функції x = 1, тобто в даній точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 2.
Методом виключення можемо визначити, що графік функції Г відповідає графік похідної під номером 1.
Відповідь: 3421.
Варіант 14МБ3
Алгоритм виконання для кожної з функцій:
- Визначити проміжки зростання та зменшення функцій.
- Визначити точки максимуму та точки мінімуму функцій.
- Зробити висновки, поставити у відповідність запропоновані графіки.
Рішення:
Проаналізуємо графік функції А.
Якщо функція зростає, то похідна позитивна і навпаки. Похідна функції дорівнює нулю в точках екстремуму.
Точка екстремуму – це точка, у якій досягається максимальне чи мінімальне значення функції.
Спочатку функція А збільшується, тобто. похідна позитивна. Цьому відповідають графіки похідних 3 і 4. У точці максимуму функції x=0, тобто в цій точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 4.
Проаналізуємо графік функції Б.
Спочатку функція Б зменшується, тобто. похідна негативна. Цьому відповідають графіки похідних 1 і 2. Точка мінімуму функції x=-1, тобто в даній точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 2.
Проаналізуємо графік функції.
Спочатку функція В зменшується, тобто. похідна негативна. Цьому відповідають графіки похідних 1 і 2. Точка мінімуму функції x = 0, тобто в даній точці похідна повинна дорівнювати нулю. Цій умові відповідає графік під номером 1.
Методом виключення можемо визначити, що графік функції Г відповідає графік похідної під номером 3.
Відповідь: 4213.
Варіант 14МБ4
На малюнку зображено графік функції та дотичні, проведені до нього у точках з абсцисами А, В, С та D.У правому стовпці вказані значення похідної в точках А, В, С та D. Користуючись графіком, поставте у відповідність кожній точці значення похідної функції в ній.

ТОЧКИ
А
У
З
D
ЗНАЧЕННЯ ВИРОБНИЧОЇ
1) –4
2) 3
3) 2/3
4) -1/2
Згадаймо, що означає похідна, а саме її значення в точці значення функції похідної у точці дорівнює тангенсу кута нахилу (коефіцієнту) дотичної.
У відповідях у нас є два позитивні, і два негативні варіанти. Як ми пам'ятаємо, якщо коефіцієнт прямої (графіка y = kx+b) Позитивний - то пряма зростає, якщо ж він негативний - то пряма зменшується.
Зростаючих прямих у нас дві — у точці A і D. Тепер пригадаємо, що означає значення коефіцієнта k?
Коефіцієнт k показує, наскільки швидко зростає чи зменшується функція (насправді коефіцієнт k сам є похідною функції y = kx+ b).
Тому k = 2/3 відповідає більш пологій прямий - D, а k = 3 - A.
Аналогічно і у випадку з від'ємними значеннями: точці B відповідає більш крута пряма з k = - 4, а точці С - -1/2.
Варіант 14МБ5
На малюнку крапками показані обсяги місячних продажів обігрівачів у магазині побутової техніки. По горизонталі вказуються місяці, по вертикалі – кількість проданих обігрівачів. Для наочності точки з'єднані лінією.

Користуючись малюнком, поставте у відповідність кожному із зазначених періодів часу характеристику продажів обігрівачів.

Алгоритм виконання
Аналізуємо частини графіка, що відповідають різним пір року. Формулюємо ситуації, що відображаються на графіку. Знаходимо їм найбільш підходящі варіанти відповідей.
Рішення:
Взимку кількість продажів перевищила 120 шт./міс., причому вона постійно збільшувалася. Ця ситуація відповідає варіанту відповіді №3. Тобто. отримуємо: А-3.
Навесні продажі поступово впали зі 120 обігрівачів за місяць до 50. Найбільш наближеним до цього формулювання є варіант №2. Маємо: Б-2.
Влітку кількість продажів не змінювалася і була мінімальною. 2-а частина цього формулювання не відбито у відповідях, а першої підходить лише №4. Звідси маємо: В 4.
Восени продажі зростали, проте їх кількість в жодному з місяців не перевищила 100 штук. Ця ситуація описана у варіанті №1. Отримуємо: Г-1.
Варіант 14МБ6
На графіку зображено залежність швидкості руху рейсового автобуса від часу. На вертикальній осі відзначено швидкість автобуса в км/год, на горизонтальній - час у хвилинах, що минув з початку руху автобуса.

Користуючись графіком, поставте у відповідність до кожного інтервалу часу характеристику руху автобуса на цьому інтервалі.

Алгоритм виконання
- Визначаємо ціну поділу на горизонтальній та на вертикальній шкалі.
- Аналізуємо по черзі запропоновані твердження 1–4 із правої колонки («Характеристики»). Зіставляємо їх з часовими інтервалами з лівої колонки таблиці, знаходимо пари «літера-число» для відповіді.
Рішення:
Ціна поділу горизонтальної шкали становить 1 с, вертикальної – 20 км/год.
- Коли автобус робить зупинку, його швидкість дорівнює 0. Нульову швидкість протягом 2 хвилин поспіль автобус мав лише з 9-ї по 11-у хвилину. Цей час потрапляє до інтервалу 8–12 хв. Отже, маємо пару для відповіді: Б-1.
- Швидкість 20 км/год і більше автобуса мала протягом декількох тимчасових проміжків. Причому варіант А тут не підходить, тому що, наприклад, на 7-й хвилині швидкість становила 60 км/год, варіант Б – тому що він уже застосований, варіант Г – тому що на початку та наприкінці проміжку автобус мав нульову швидкість . В даному випадку підходить варіант (12-16 хв); на цьому проміжку автобус починає рух зі швидкістю 40 км/год, далі прискорюється до 100 км/м і потім поступово знижує швидкість до 20 км/год. Отже, маємо: В 2.
- Тут встановлено обмеження швидкості. При цьому варіанти Б та В ми не розглядаємо. Інші інтервали А і Г, що залишилися, підходять обидва. Тому правильно буде розглянути спочатку 4-й варіант, а потім знову повернутися до 3-го.
- З двох інтервалів, що залишилися, для характеристики №4 підходить лише 4–8 хв, оскільки на цьому проміжку зупинка була (на 6-й хвилині). На проміжку 18–22 хв зупинок не було. Отримуємо: А-4. Звідси випливає, що з характеристики №3 необхідно взяти інтервал Р, тобто. виходить пара Г-3.
Варіант 14МБ7
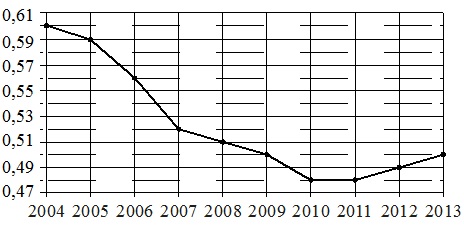
На малюнку крапками показано приріст населення Китаю в період з 2004 по 2013 рік. По горизонталі вказується рік, по вертикалі – приріст населення у відсотках (збільшення чисельності населення щодо минулого року). Для наочності точки з'єднані лінією.
Користуючись малюнком, поставте у відповідність кожному із зазначених періодів часу характеристику приросту населення Китаю в цей період.

Алгоритм виконання
- Визначаємо ціну поділу вертикальної шкали малюнка. Знаходиться вона як різниця пари сусідніх значень шкали, поділена на 2 (бо між двома сусідніми значеннями є 2 поділки).
- Аналізуємо послідовно наведені за умови характеристики 1–4 (ліва таблична колонка). Зіставляємо кожну з них із конкретним періодом часу (права таблична колонка).
Рішення:
Ціна поділу вертикальної шкали становить 0,01%.
- Падіння приросту безперервно тривало з 2004 до 2010 року. У 2010–2011 роках приріст був стабільно мінімальним, і з 2012 року він почав збільшуватися. Тобто. зупинка приросту сталася у 2010 році. Цей рік перебуває у періоді 2009–2011 років. Відповідно, маємо: В 1.
- Найбільшим падінням приросту слід вважати «круто» падаючу лінію графіка на малюнку. Вона припадає на період 2006-2007 років. і становить 0,04%, за рік (0,59–0,56=0,04% у 2006 р. та 0,56–0,52=0,04% у 2007 р.). Звідси отримуємо: А-2.
- Зазначений у характеристиці №3 приріст розпочався з 2007 року, продовжився у 2008 р. та завершився у 2009 році. Це відповідає періоду часу Б, тобто. маємо: Б-3.
- Приріст населення почав зростати після 2011 р., тобто. у 2012–2013 роках. Тому отримуємо: Г-4.
Варіант 14МБ8
На малюнку зображено графік функції та дотичні, проведені до нього в точках з абсцис А,В,С і D.

У правому стовпці вказані значення похідної функції у точках А, В, С і D. Користуючись графіком, поставте у відповідність кожній точці значення похідної функції у ній.

Алгоритм виконання
- Розглядаємо пару дотичних, що мають гострий кут з покладеним напрямом осі абсцис. Порівнюємо їх, знаходимо відповідність серед кількох відповідних значень похідних.
- Розглядаємо пару дотичних, що утворюють з покладеним напрямом осі абсцис тупий кут. Порівнюємо їх за модулем, визначаємо відповідність їх значенням похідних серед двох, що залишилися у правій колонці.
Рішення:
Гострий кут з положит.напрямком осі абсцис утворюють похідні в т.в і т.с. Ці похідні мають поклад.значення. Тому вибирати тут слід між значеннями №№1 і 3. Застосовуючи правило про те, що якщо кут менше 45 0 то похідна менше 1, а якщо більше, то більше 1, робимо висновок: в т.В похідна по модулю більше 1, в т.з – менше 1. Це означає, що можна скласти пари для відповіді: У 3і З 1.
Похідні в т.А і т.D утворюють з положит.напрямком осі абсцис тупий кут. І тут застосовуємо те саме правило, трохи перефразувавши його: чим більша дотична в точці «притиснута» до лінії осі абсцис (до запереч. її напрямку), тим більше вона за модулем. Тоді отримуємо: похідна т.а. по модулю менше, ніж похідна т.d. Звідси маємо пари для відповіді: А-2і D-4.
Варіант 14МБ9
На малюнку крапками показано середньодобову температуру повітря в Москві в січні 2011 року. По горизонталі вказуються числа місяця, по вертикалі – температура градусів Цельсія. Для наочності точки з'єднані лінією.

Користуючись малюнком, поставте у відповідність кожному із зазначених періодів часу характеристику зміни температури.

Алгоритм виконання
Аналізуємо послідовно характеристики 1-4 (права колонка), використовуючи графік малюнку. Ставимо кожній з них у відповідність конкретний часовий період (ліва колонка).
Рішення:
- Зростання температури спостерігалося лише наприкінці періоду 22–28 січня. Тут 27 та 28 числа вона підвищувалася відповідно на 1 та на 2 градуси. Наприкінці періоду 1–7 січня температура була стабільною (–10 градусів), наприкінці 8–14 та 15–21 січня знижувалася (з –1 до –2 та з –11 до –12 градусів відповідно). Тому отримуємо: Г-1.
- Оскільки кожен тимчасовий період охоплює 7 днів, то потрібно аналізувати температуру, починаючи з 4-го дня кожного періоду. Незмінною протягом 3–4 днів температура була лише з 4 до 7 січня. Тому отримуємо відповідь: А-2.
- Місячний мінімум температури спостерігався 17 січня. Це число входить у період 15–21 січня. Звідси маємо пару: У 3.
- Температурний максимум припав 10 січня і становив +1 градус. Ця дата потрапляє у період 8–14 січня. Отже, маємо: Б-4.
Варіант 14МБ10
Алгоритм виконання
- Значення функції в точці позитивне, якщо ця точка розташована вище за осю Ох.
- Похідна в точці більша за нуль, якщо дотична до цієї точки утворює гострий кут з позитивним напрямом осі Ох.
Рішення:
Точка А. Вона перебуває нижче осі Ох, отже значення функції у ній негативно. Якщо провести у ній дотичну, то кут між нею і положит.направлением Ох становитиме близько 90 0 , тобто. утворює гострий кут. Отже, у разі підходить характеристика №3. Тобто. маємо: А-3.
Крапка Б. Вона перебуває над віссю Ох, тобто. точка має покласти значення функції. Стосовно цієї точки буде досить близько «прилягати» до осі абсцис, утворюючи тупий кут (трохи менше 180 0) з позитивним її напрямом. Відповідно, похідна у цій точці негативна. Т.ч., тут підходить характеристика 1. Отримуємо відповідь: В 1.
Точка С. Точка розташована нижче осі Ох, дотична в ній утворює великий тупий кут з покладеним напрямом осі абсцис. Тобто. в т.з значення і функції, і похідної негативно, що відповідає характеристиці №2. Відповідь: С-2.
Точка D. Точка знаходиться вище осі Ох, а дотична в ній утворює з покладеним напрямом осі гострий кут. Це свідчить, що значення функції, і значення похідної тут більше нуля. Відповідь: D-4.
Варіант 14МБ11
На малюнку крапками показано обсяги місячних продажів холодильників у магазині побутової техніки. По горизонталі вказуються місяці, по вертикалі кількість проданих холодильників. Для наочності точки з'єднані лінією.

Користуючись малюнком, поставте у відповідність кожному із зазначених періодів часу характеристику продажу холодильників.
Пряма y=3x+2 є дотичною до графіка функції y=-12x^2+bx-10. Знайдіть b , враховуючи, що абсцис точки дотику менший за нуль.
Показати рішенняРішення
Нехай x_0 - абсцис точки на графіку функції y = -12x ^ 2 + bx-10, через яку проходить дотична до цього графіка.
Значення похідної у точці x_0 дорівнює кутовому коефіцієнту дотичної, тобто y"(x_0)=-24x_0+b=3. З іншого боку, точка дотику належить одночасно і графіку функції і дотичної, тобто -12x_0^2+bx_0-10= 3x_0 + 2. Отримуємо систему рівнянь \begin(cases) -24x_0+b=3,\-12x_0^2+bx_0-10=3x_0+2. \end(cases)
Вирішуючи цю систему, отримаємо x_0^2=1, отже або x_0=-1, або x_0=1. Згідно з умовою абсцис точки торкання менше нуля, тому x_0=-1, тоді b=3+24x_0=-21.
Відповідь
Умова
На малюнку зображено графік функції y=f(x) (що є ламаною лінією, що складається з трьох прямолінійних відрізків). Користуючись малюнком, обчисліть F(9)-F(5), де F(x) — одна з першорядних функцій f(x).
Показати рішенняРішення
За формулою Ньютона-Лейбніца різниця F(9)-F(5), де F(x) — одна з первісних функцій f(x), дорівнює площі криволінійної трапеції, обмеженої графіком функції y=f(x), прямими y=0 , x=9 та x=5. За графіком визначаємо, що зазначена криволінійна трапеція є трапецією з основами, рівними 4 і 3 та висотою 3 .
Її площа дорівнює \frac(4+3)(2)\cdot 3=10,5.
Відповідь
Джерело: «Математика. Підготовка до ЄДІ-2017. Профільний рівень». За ред. Ф. Ф. Лисенка, С. Ю. Кулабухова.
Умова
На малюнку зображено графік y=f"(x) — похідної функції f(x), визначеної на інтервалі (-4; 10). Знайдіть проміжки зменшення функції f(x). У відповіді вкажіть довжину найбільшого з них.

Рішення
Як відомо, функція f(x) зменшується на тих проміжках, у кожній точці яких похідна f"(x) менша за нуль. Враховуючи, що треба знаходити довжину найбільшого з них природно по малюнку виділяються три такі проміжки: (-4; -2) (0; 3);(5; 9).
Довжина найбільшого з них (5; 9) дорівнює 4.
Відповідь
Джерело: «Математика. Підготовка до ЄДІ-2017. Профільний рівень». За ред. Ф. Ф. Лисенка, С. Ю. Кулабухова.
Умова
На малюнку зображено графік y=f"(x) — похідну функцію f(x), визначену на інтервалі (-8; 7). Знайдіть кількість точок максимуму функції f(x), що належать проміжку [-6; -2].
.png)
Рішення
З графіка видно, що похідна f"(x) функції f(x) змінює знак з плюсу на мінус (саме в таких точках буде максимум) рівно в одній точці (між -5 і -4) з проміжку [-6; -2 ] Тому на проміжку [-6;-2] рівно одна точка максимуму.
Відповідь
Джерело: «Математика. Підготовка до ЄДІ-2017. Профільний рівень». За ред. Ф. Ф. Лисенка, С. Ю. Кулабухова.
Умова
На малюнку зображено графік функції y=f(x), визначеної на інтервалі (-2; 8). Визначте кількість точок, у яких похідна функції f(x) дорівнює 0 .

Рішення
Рівність похідної нулю в точці означає, що дотична до графіка функції, проведена в цій точці, паралельна осі Ox. Тому знаходимо такі точки, у яких дотична до графіка функції паралельна осі Ox. На цьому графіку такими точками є точки екстремуму (точки максимуму чи мінімуму). Як бачимо, точок екстремуму 5 .
Відповідь
Джерело: «Математика. Підготовка до ЄДІ-2017. Профільний рівень». За ред. Ф. Ф. Лисенка, С. Ю. Кулабухова.
Умова
Пряма y=-3x+4 паралельна до графіки функції y=-x^2+5x-7. Знайдіть абсцис точки торкання.
Показати рішенняРішення
Кутовий коефіцієнт прямий до графіка функції y=-x^2+5x-7 у довільній точці x_0 дорівнює y"(x_0). Але y"=-2x+5, отже, y"(x_0)=-2x_0+5. Кутовий коефіцієнт прямої y=-3x+4, вказаної в умові, дорівнює -3.Паралельні прямі мають однакові кутові коефіцієнти, тому знаходимо таке значення x_0, що =-2x_0 +5=-3.
Отримуємо: x_0 = 4.
Відповідь
Джерело: «Математика. Підготовка до ЄДІ-2017. Профільний рівень». За ред. Ф. Ф. Лисенка, С. Ю. Кулабухова.
Умова
На малюнку зображено графік функції y = f (x) і відзначені точки -6, -1, 1, 4 на осі абсцис. У якій із цих точок значення похідної найменше? У відповіді вкажіть цю точку.






















































 Назад вперед
Назад вперед
Увага! Попередній перегляд слайдів використовується виключно для ознайомлення та може не давати уявлення про всі можливості презентації. Якщо вас зацікавила ця робота, будь ласка, завантажте повну версію.
Тип уроку:повторення та узагальнення.
Форма уроку:урок-консультація.
Цілі уроку:
- навчальна: повторити та узагальнити теоретичні знання за темами: "Геометричний зміст похідної" та "Застосування похідної до дослідження функцій"; розглянути всі типи завдань В8, що зустрічаються на ЄДІ з математики; надати учням можливість перевірити свої знання за самостійного вирішення завдань; навчити заповнювати екзаменаційний бланк відповідей;
- розвиваюча: сприяти розвитку спілкування як методу наукового пізнання, смислової пам'яті та довільної уваги; формування таких ключових компетенцій, як порівняння, зіставлення, класифікація об'єктів, визначення адекватних способів вирішення навчальної задачі на основі заданих алгоритмів, здатність самостійно діяти в ситуації невизначеності, контролювати та оцінювати свою діяльність, знаходити та усувати причини труднощів, що виникли;
- виховна: розвивати в учнів комунікативні компетенції (культуру спілкування, вміння працювати у групах); сприяти розвитку потреби до самоосвіти.
Технології: навчання, ІКТ.
Методи навчання:словесний, наочний, практичний, проблемний.
Форми роботи:індивідуальна, фронтальна, групова.
Навчально-методичне забезпечення:
1. Алгебра та початку математичного аналізу.11 клас: навч. Для загальноосвіт. Установ: базовий та профіль. рівні / (Ю. М. Колягін, М. В. Ткачова, Н. Є. Федорова, М. І. Шабунін); за редакцією А. Б. Жижченко. - 4-те вид. - М.: Просвітництво, 2011.
2. ЄДІ: 3000 завдань із відповідями з математики. Усі завдання групи В/О.Л. Семенов, І.В. Ященко та ін.; за редакцією А.Л. Семенова, І.В. Ященко. - М.: Видавництво "Іспит", 2011.
3. Відкритий банк завдань.
Обладнання та матеріали для уроку:проектор, екран, ПК для кожного учня із встановленою на нього презентацією, для всіх, хто навчається, роздруківка пам'ятки (Додаток 1)та оціночний лист ( Додаток 2) .
Попередня підготовка до уроку:як домашнього завдання учням пропонується повторити за підручником теоретичний матеріал на теми: “Геометричний сенс похідної”, “Застосування похідної до вивчення функцій”; клас розбивається на групи (по 4 особи), у кожній з яких навчаються різних рівнів.
Пояснення до уроку:Цей урок проводиться в 11 класі на етапі повторення та підготовки до ЄДІ. Урок націлений на повторення та узагальнення теоретичного матеріалу, застосування його при вирішенні екзаменаційних завдань. Тривалість уроку – 1,5 години .
Цей урок не прикріплений до підручника, тому може проводитися під час роботи з будь-якого УМК. Також цей урок можна розбити на два окремих і провести їх як підсумкові уроки з тем, що розглядаються.
Хід уроку
I. Організаційний момент.
ІІ. Постановка цілей уроку.
ІІІ. Повторення на тему “Геометричний сенс похідної”.
Усна фронтальна робота із використанням проектора (слайди №3-7)
Робота у групах: розв'язання завдань з підказками, відповідями, з консультацією вчителя (слайди №8-17)
IV. Самостійна робота 1.
Учні працюють індивідуально на ПК (слайди № 18-26), свої відповіді заносять до оцінного листа. Якщо необхідно, можна взяти консультацію вчителя, але у разі учень втратить 0,5 бала. Якщо учень впорається з роботою раніше, він може вибрати на вирішення додаткові завдання зі збірки , стр.242, 306-324 (додаткові завдання оцінюються окремо).
V. Взаємоперевірка.
Учні обмінюються оціночними листами, перевіряють роботу товариша, виставляють бали (слайд №27)
VI. Корекція знань.
VII. Повторення на тему “Застосування похідної дослідження функцій”
Усна фронтальна робота із використанням проектора (слайди №28-30)
Робота в групах: розв'язання задач з підказками, відповідями, з консультацією вчителя (слайди №31-33)
VIII. Самостійна робота 2.
Учні працюють індивідуально на ПК (слайди №34-46), свої відповіді заносять до бланку відповідей. Якщо необхідно, можна взяти консультацію вчителя, але у разі учень втратить 0,5 бала. Якщо учень впорається з роботою раніше, він може вибрати для вирішення додаткові завдання зі збірки , стор.243-305 (додаткові завдання оцінюються окремо).
IX. Взаємоперевірка.
Учні обмінюються оціночними листами, перевіряють роботу товариша, виставляють бали (слайд № 47).
X. Корекція знань.
Учні знову працюють у своїх групах, обговорюють рішення, виправляють помилки.
XI. Підведення підсумків.
Кожен учень підраховує свої бали та виставляє в оціночний лист оцінку.
Учні здають вчителю оціночний лист і вирішення додаткових завдань.
Кожен учень отримує пам'ятку (слайд №53-54).
XII. Рефлексія.
Учням пропонується оцінити свої знання, вибравши одну з фраз:
- У мене все вийшло!!!
- Треба вирішити ще кілька прикладів.
- Ну, хто придумав цю математику!
XIII. Домашнє завдання.
Для домашньої роботи учням пропонується вибрати на вирішення завдання зі збірки , стор. 242-334, і навіть з відкритого банку завдань.
Для початку спробуй знайти область визначення функції:
Впорався? Порівняємо відповіді:
Все вірно? Молодець!
Тепер спробуємо знайти область значень функції:

Знайшов? Порівнюємо:
Зійшлося? Молодець!
Ще раз попрацюємо з графіками, тільки тепер трохи складніше - знайти і область визначення функції, і область значень функції.
Як знайти область визначення і область значень функції (просунутий варіант)

Ось що вийшло:
З графіками, я гадаю, ти розібрався. Тепер спробуємо відповідно до формул знайти область визначення функції (якщо ти не знаєш як це зробити, прочитай розділ про ):
Впорався? Звіримо відповіді:
- , так як підкорене вираз має бути більше або дорівнює нулю.
- , Так як на нуль ділити не можна і підкорене вираз не може бути негативним.
- , оскільки відповідно при всіх.
- , Так як на нуль ділити не можна.
Однак у нас залишився ще один нерозібраний момент.
Ще раз повторю визначення і зроблю на ньому акцент:
Помітив? Слово «єдиний» - це дуже важливий елемент нашого визначення. Постараюся пояснити тобі на пальцях.
Допустимо, у нас є функція, задана прямою. . При, ми підставляємо це значення в наше «правило» і отримуємо, що. Одному значенню відповідає одне значення. Ми навіть можемо скласти таблицю різних значень і побудувати графік цієї функції, щоб у цьому.
«Дивися! - скажеш ти, - «» зустрічається двічі!» Так можливо парабола не є функцією? Ні, є!
Те, що «» зустрічається двічі далеко не привід звинувачувати параболу у неоднозначності!
Справа в тому, що, при розрахунку для, ми отримали один гравець. І при розрахунку ми отримали один гравець. Так що все правильно, парабола є функцією. Подивися на графік:

Розібрався? Якщо ні, ось тобі життєвий приклад зовсім далекий від математики!
Припустимо, у нас є група абітурієнтів, які познайомилися під час подачі документів, кожен із яких у розмові розповів, де він живе.

Погодься, цілком реально, що кілька хлопців живуть в одному місті, але неможливо, щоб одна людина жила в кількох містах одночасно. Це ніби логічне уявлення нашої «параболи» - декільком різним ікс відповідає один і той же гравець.
Тепер вигадаємо приклад, коли залежність не буде функцією. Припустимо, ці ж хлопці розповідали, на які спеціальності вони подали документи:

Тут у нас зовсім інша ситуація: одна людина може спокійно подати документи як на один, так і на кілька напрямків. Тобто одному елементубезлічі ставиться у відповідність кілька елементівмножини. Відповідно, це функція.
Перевіримо твої знання практично.
Визнач за малюнками, що є функцією, а що ні:

Розібрався? А ось і відповіді:
- Функцією є - В,Є.
- Функцією не є – А, Б, Г, Д.
Ти спитаєш чому? Та ось чому:

На всіх малюнках крім в)і Е)на один доводиться кілька!
Впевнена, тепер, ти з легкістю відрізниш функцію від функції, скажеш, що таке аргумент і що таке залежна змінна, а так само визначиш область допустимих значень аргументу і область визначення функції. Приступаємо до наступного розділу – як задати функцію?
Способи завдання функції
Як ти вважаєш, що означають слова "задати функцію"? Правильно, це означає пояснити всім охочим, про яку функцію в даному випадку йдеться. Причому пояснити так, щоб кожен зрозумів тебе правильно і намальовані людьми на твоє пояснення графіки функцій були однакові.
Як це можна зробити? Як встановити функцію?Найпростіший спосіб, який вже не раз застосовувався у цій статті за допомогою формули.Ми пишемо формулу, і, підставляючи у ній значення, обчислюємо значення. А як ти пам'ятаєш, формула - це закон, правило, за яким нам та іншій людині стає ясно, як ікс перетворюється на ігрек.
Зазвичай, саме так і роблять - у завданнях ми бачимо вже готові функції, задані формулами, однак, існують інші способи задати функцію, про які всі забувають, у зв'язку з чим питання «як ще можна задати функцію?» ставить у глухий кут. Розберемося у всьому порядку, а почнемо з аналітичного способу.
Аналітичний спосіб завдання функції
Аналітичний спосіб і є завдання функції з допомогою формули. Це універсальний і вичерпний і однозначний спосіб. Якщо у тебе є формула, то ти знаєш про функцію абсолютно все – ти можеш скласти по ній табличку значень, можеш побудувати графік, визначити, де функція зростає, а де зменшується, загалом, дослідити її за повною програмою.
Розглянемо функцію. Чому одно?
"Що це означає?" - Запитаєш ти. Зараз поясню.
Нагадаю, що у записі вираз у дужках називається аргументом. І цей аргумент може бути будь-яким виразом, не обов'язково простим. Відповідно, яким би не був аргумент (вираз у дужках), ми його запишемо натомість у виразі.
У нашому прикладі вийде так:
Розглянемо ще завдання, пов'язане з аналітичним способом завдання функції, яке буде на іспиті.
Знайдіть значення виразу, при.
Впевнена, що спочатку, ти злякався, побачивши такий вираз, але в ньому немає нічого страшного!
Все як і в минулому прикладі: яким би не був аргумент (вираз у дужках), ми його запишемо натомість у виразі. Наприклад, для функції.
Що ж потрібно зробити у нашому прикладі? Замість треба написати, а замість - :
скоротити вираз, що вийшов:
От і все!
Самостійна робота
Тепер спробуй самостійно знайти значення наступних виразів:
- , якщо
- , якщо
Впорався? Порівняємо наші відповіді: Ми звикли, що функція має вигляд
Навіть у наших прикладах ми задаємо функцію саме таким чином, проте аналітично можна задати функцію у неявному вигляді, наприклад.
Спробуй збудувати цю функцію самостійно.
Впорався?
Ось як будувала її я.
Яке рівняння ми вивели?
Правильно! Лінійне, а це означає, що графіком буде пряма лінія. Зробимо табличку, щоб визначити, які точки належать нашій прямій:
Ось саме те, про що ми говорили... Одному відповідає кілька.
Спробуємо намалювати те, що вийшло:

Чи є те, що ми отримали функцією?
Правильно, ні! Чому? Спробуй відповісти на це запитання малюнком. Що в тебе вийшло?

«Оскільки одному значенню відповідає кілька значень!»
Який висновок ми можемо зробити з цього?
Правильно, функція не завжди може бути виражена явно, і не завжди те, що замасковано під функцію є функцією!
Табличний спосіб завдання функції
Як випливає з назви, цей спосіб є простою табличкою. Так Так. На кшталт тієї, якою ми з тобою вже становили. Наприклад:
Тут ти одразу помітив закономірність – ігорок утричі більший за ікс. А тепер завдання на «дуже добре подумати»: як ти вважаєш, чи функція, задана у вигляді таблиці, функції?
Не будемо довго міркувати, а малюватимемо!
Отже. Малюємо функцію, задану шпалерами способами:

Бачиш різницю? Справа зовсім не у зазначених точках! Придивись уважніше:

Тепер побачив? Коли ми задаємо функцію табличним способом, ми на графіку відображаємо лише ті точки, які є у нас у таблиці, і лінія (як у нашому випадку) проходить лише через них. Коли ми задаємо функцію аналітичним способом, ми можемо взяти будь-які точки і наша функція ними не обмежується. Ось така особливість. Запам'ятай!
Графічний спосіб побудови функції
Графічний спосіб побудови функції не менш зручний. Ми малюємо нашу функцію, а інша зацікавлена людина може знайти чому дорівнює ігорок при певному ікс і так далі. Графічний та аналітичний методи одні з найпоширеніших.
Однак тут потрібно пам'ятати про що ми з тобою говорили на самому початку - не кожна «загогулина» намальована в системі координат є функцією! Згадав? Про всяк випадок скопіюю тобі сюди визначення, що функцією є:
Як правило, люди зазвичай називають саме ті три способи завдання функції, які ми розібрали – аналітичний (за допомогою формули), табличний та графічний, геть-чисто забуваючи про те, що функцію можна словесно описати. Як це? Так, дуже просто!
Словесний опис функції
Як описати функцію словесно? Візьмемо наш недавній приклад. Цю функцію можна описати «кожного дійсного значення ікс відповідає його потрійне значення». От і все. Нічого складного. Ти, звичайно, заперечиш - «є настільки складні функції, які словесно поставити просто неможливо!» Так, є такі, але є функції, які описати словесно легше, ніж задати формулою. Наприклад: "кожному натуральному значенню ікс відповідає різниця між цифрами, з яких він складається, при цьому за зменшуване береться найбільша цифра, що міститься в записі числа". Тепер розглянемо, як наш словесний опис функції реалізується практично:
Найбільша цифра в даному числі - відповідно - зменшуване, тоді:
Основні види функцій
Тепер перейдемо до найцікавішого - розглянемо основні види функцій, з якими ти працював/працюєш і працюватимеш в курсі шкільної та інститутської математики, тобто познайомимося з ними, так би мовити, і дамо їм коротку характеристику. Докладніше про кожну функцію читай у відповідному розділі.
Лінійна функція
Функція виду, де - дійсні числа.
Графіком цієї функції служить пряма, тому побудова лінійної функції зводиться до знаходження координат двох точок.
Положення прямої на координатній площині залежить від кутового коефіцієнта.

Область визначення функції (як область допустимих значень аргументу) - .
Область значень - .
Квадратична функція
Функція виду, де
Графіком функції є парабола, при гілки параболи спрямовані вниз, при вгору.
Багато властивостей квадратичної функції залежить від значення дискримінанта. Дискримінант обчислюється за формулою
Положення параболи на координатній площині щодо значення та коефіцієнта показано на малюнку:

Область визначення
Область значень залежить від екстремуму цієї функції (точки вершини параболи) та коефіцієнта (напрямки гілок параболи)
Зворотня пропорційність
Функція, що задається формулою, де
Число називається коефіцієнтом зворотної пропорційності. Залежно від того, яке значення, гілки гіперболи знаходяться у різних квадратах:

Область визначення - .
Область значень - .
КОРОТКИЙ ВИКЛАД І ОСНОВНІ ФОРМУЛИ
1. Функцією називається правило, за яким кожному елементу множини ставиться у відповідність єдиний елемент множини.
- - це формула, що означає функцію, тобто залежність однієї змінної від іншої;
- - змінна величина, або аргумент;
- - Залежна величина - змінюється при зміні аргументу, тобто згідно з якоюсь певною формулою, що відображає залежність однієї величини від іншої.
2. Допустимі значення аргументу, чи область визначення функції - те, що пов'язані з можливими, у яких функція має сенс.
3. Область значень функції- це те, які значення набуває, при допустимих значеннях.
4. Існує 4 способи завдання функції:
- аналітичний (за допомогою формул);
- табличний;
- графічний
- словесний опис.
5. Основні види функцій:
- : , де, - дійсні числа;
- : , де;
- : , де.



