Перетворення графіків. Перетворення графіків елементарних функцій

Основні елементарні функції у чистому вигляді без перетворення зустрічаються рідко, тому найчастіше доводиться працювати з елементарними функціями, які отримали з основних за допомогою додавання констант та коефіцієнтів. Такі графіки будуються з допомогою геометричних перетворень заданих елементарних функций.

Розглянемо на прикладі квадратичної функції виду y = - 1 3 x + 2 3 2 + 2 , графіком якої є парабола y = x 2 , яка стиснута втричі щодо О у і симетрична щодо О х, причому зсунуту на 2 3 по О х вправо, на 2 одиниці по О у вгору. На координатній прямій це виглядає так:

Yandex.RTB R-A-339285-1

Геометричні перетворення графіка функції

Застосовуючи геометричні перетворення заданого графіка, отримуємо, що графік зображується функцією виду ± k 1 · f (± k 2 · (x + a)) + b , коли k 1 > 0 , k 2 > 0 є коефіцієнтами стиснення при 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 вздовж О у і О х. Знак перед коефіцієнтами k 1 і k 2 говорить про симетричне відображення графіка щодо осей, a і b зрушують її по О х і О у.

Визначення 1

Існує 3 види геометричних перетворень графіка:

• Масштабуваннявздовж Ох і О у. На це впливають коефіцієнти k 1 і k 2 за умови не рівності 1 коли 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1 , k 2 > 1 то графік розтягується по О у і стискається по О х.
• Симетричне відображення щодо координатних осей.За наявності знака «-» перед k 1 симетрія йде щодо Ох, перед k 2 йде щодо О у. Якщо «-» відсутня, то пункт при рішенні пропускається;
• Паралельне перенесення (зсув)вздовж Ох і О у. Перетворення проводиться за наявності коефіцієнтів a та b нерівних 0 . Якщо значення a позитивне, до графіка зсувається вліво на | а | одиниць, якщо негативне a , тоді право на таку ж відстань. Значення b визначає рух по осі О, що означає при позитивному b функція рухається вгору, при негативному - вниз.

Розглянемо рішення на прикладах, починаючи зі статечної функції.

Приклад 1

Перетворити y = x 2 3 та побудувати графік функції y = - 1 2 · 8 x - 4 2 3 + 3 .

Рішення

Представимо функції таким чином:

y = - 1 2 · 8 x - 4 2 3 + 3 = - 1 2 · 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Де k 1 = 2 варто звернути увагу на наявність « - » , а = - 1 2 , b = 3 . Звідси отримуємо, що геометричні перетворення виробляються з розтягування вздовж О у вдвічі, відображається симетрично щодо Ох, зрушується вправо на 12 і вгору на 3 одиниці.

Якщо зобразити початкову статечну функцію, отримаємо, що

при розтягуванні вдвічі вздовж О маємо, що

Відображення, симетричне щодо Ох, має вигляд

а рух праворуч на 1 2

рух на 3 одиниці вгору має вигляд

Перетворення показової функції розглянемо з прикладів.

Приклад 2

Зробити побудову графіка показової функції y = - 1 2 1 2 (2 - x) + 8 .

Рішення.

Перетворимо функцію, виходячи з властивостей статечної функції. Тоді отримаємо, що

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 · 1 2 - 1 2 x + 8

Звідси видно, що отримаємо ланцюжок перетворень y = 1 2 x:

y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = - 1 2 · 1 2 1 2 x → y = - 1 2 · 1 2 - 1 2 x → → y = - 1 2 · 1 2 - 1 2 x + 8

Виходить, що вихідна показова функція має вигляд

Стискання вдвічі вздовж О у дає

Розтягування вздовж Ох

Симетричне відображення щодо Ох

Відображення симетрично щодо О у

Зрушення на 8 одиниць нагору

Розглянемо рішення з прикладу логарифмічної функції y = ln (x) .

Приклад 3

Побудувати функцію y = ln e 2 · - 1 2 x 3 за допомогою перетворення y = ln (x).

Рішення

Для вирішення необхідно використовувати властивості логарифму, тоді отримуємо:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Перетворення логарифмічної функції мають такий вигляд:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Зобразимо графік вихідної логарифмічної функції

Виробляємо стискання ладу по О у

Виробляємо розтягування вздовж Ох

Виробляємо відображення щодо О у

Виконуємо зрушення вгору на 2 одиниці, отримуємо

Для перетворення графіків тригонометричної функції необхідно підганяти під схему розв'язання виду ± k 1 · f (± k 2 · (x + a)) + b . Необхідно, щоб k 2 дорівнював T k 2 . Звідси отримуємо, що 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Розглянемо приклади розв'язання завдань із перетвореннями y = sin x .

Приклад 4

Побудувати графік y = - 3 sin 1 2 x - 3 2 - 2 за допомогою перетворень функції y = sinx.

Рішення

Необхідно привести функцію до виду ± k 1 · f ± k 2 · x + a + b. Для цього:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Видно, що k 1 = 3 k 2 = 1 2 a = - 3 b = - 2 . Оскільки перед k 1 є « - » , а перед k 2 - немає, тоді отримаємо ланцюжок перетворень виду:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Детальне перетворення синусоїди. При побудові графіка вихідної синусоїди y = sin (x) отримуємо, що найменшим позитивним періодом вважається T = 2 π. Знаходження максимуму в точках π 2 + 2 π · k; 1, а мінімуму - - π 2 + 2 π · k; - 1, k ∈ Z.

Проводиться розтяг по О у втричі, значить зростання амплітуди коливань зросте в 3 рази. T = 2 π – це найменший позитивний період. Максимуми переходять у π 2 ​​+ 2 π · k; 3 , k ∈ Z , мінімуми - π 2 + 2 π · k ; - 3, k ∈ Z.

При розтягуванні Ох вдвічі отримуємо, що найменший позитивний період збільшується в 2 рази і дорівнює T = 2 π k 2 = 4 π . Максимуми переходять у π + 4 π · k; 3 , k ∈ Z , мінімуми – в - π + 4 π · k; - 3, k ∈ Z.

Зображення проводиться симетрично щодо х. Найменший позитивний період у разі не змінюється і дорівнює T = 2 π k 2 = 4 π . Перехід максимуму виглядає як - π + 4 π · k; 3 , k ∈ Z , а мінімуму – π + 4 π · k; - 3, k ∈ Z.

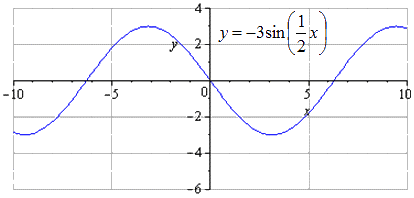
Здійснюється зміщення графіка вниз на 2 одиниці. Зміни найменшого загального періоду не відбувається. Знаходження максимумів з переходженням у точки - π + 3 + 4 π · k; 1, k ∈ Z, мінімумів - π + 3 + 4 π · k; - 5, k ∈ Z.

На цьому етапі графік тригонометричної функції вважається перетвореним.

Розглянемо докладне перетворення функції y = cos x.

Приклад 5

Побудувати графік функції y = 3 2 cos 2 - 2 x + 1 за допомогою перетворення функції виду y = cos x.

Рішення

За алгоритмом необхідно задану функцію привести до вигляду ± k 1 · f ± k 2 · x + a + b. Тоді отримуємо, що

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (-2 (x - 1)) + 1

З умови видно, що k 1 = 3 2 k 2 = 2 a = - 1 b = 1 де k 2 має «-», а перед k 1 він відсутній.

Звідси отримуємо, що вийде графік тригонометричної функції виду:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (-2 x) → → y = 3 2 cos (-2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1

Покрокове перетворення косінусоїди з графічною ілюстрацією.

При заданій графіці y = cos(x) видно, що найменший загальний період дорівнює T = 2 π. Знаходження максимумів у 2 π · k; 1, k ∈ Z, а мінімумів π + 2 π · k; - 1, k ∈ Z.

При розтягуванні вздовж О у 3 2 рази відбувається зростання амплітуди коливань у 3 2 рази. T = 2 π є найменшим позитивним періодом. Знаходження максимумів у 2 π · k; 3 2 , k ∈ Z , мінімумів π + 2 π · k ; - 3 2, k ∈ Z.

При стисканні вздовж Ох вдвічі отримуємо, що найменшим позитивним періодом є число T = 2 π k 2 = π. Проводиться перехід максимумів в π · k; 3 2, k ∈ Z, мінімум - π 2 + π · k; - 3 2, k ∈ Z.

Симетричне відображення щодо Про у. Оскільки графік непарний, він не змінюватиметься.

При зрушенні графіка на 1 . Відсутні зміни найменшого позитивного періоду T = π. Знаходження максимумів в π · k + 1; 3 2 , k ∈ Z , мінімумів - π 2 + 1 + π · k; - 3 2, k ∈ Z.

При зрушенні на 1 найменший позитивний період дорівнює T = і не змінений. Знаходження максимумів в π · k + 1; 5 2 , k ∈ Z , мінімумів π 2 + 1 + π · k ; - 1 2, k ∈ Z.

Перетворення функції косинуса завершено.

Розглянемо перетворення з прикладу y = t g x .

Приклад 6

Побудувати графік функції y = - 1 2 t g π 3 - 2 3 x + π 3 за допомогою перетворень функції y = t g (x) .

Рішення

Для початку необхідно привести задану функцію до виду ± k 1 · f ± k 2 · x + a + b , після чого отримуємо, що

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Виразно видно, що k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, а перед коефіцієнтами k 1 і k 2 є «-». Отже, після перетворення тангенсоїди отримуємо

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Поетапне перетворення тангенсоіди із графічним зображенням.

Маємо, що вихідний графік - y = t g (x) . Зміна позитивного періоду дорівнює T = π. Областю визначення вважається - π 2 + π · k; π 2 + π · k, k ∈ Z.

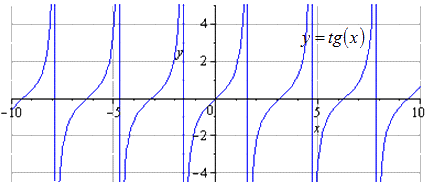
Стискаємо в 2 рази вздовж О у. T = π вважається найменшим позитивним періодом, де область визначення має вигляд - π 2 + π · k; π 2 + π · k, k ∈ Z.

Розтягуємо вздовж Ох у 3 2 рази. Обчислимо найменший позитивний період, причому дорівнював T = π k 2 = 3 2 π. А область визначення функції з координатами - 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k , k ∈ Z змінюється тільки область визначення.

Симетрія йде на бік Ох. Період не зміниться у цей момент.

Необхідно симетрично відображати осі координат. Область визначення у разі незмінна. Графік збігається із попереднім. Це свідчить, що функція тангенса непарна. Якщо до непарної функції встановити симетричне відображення О х і О у, тоді перетворимо до вихідної функції.

Гіпотеза: Якщо вивчити рух графіка при освіті рівняння функцій, то можна помітити, що всі графіки підпорядковуються загальним закономірностям, тому можна сформулювати загальні закони незалежно від функцій, що дозволить не тільки полегшити побудову графіків різних функцій, але й використовувати їх при вирішенні завдань.

Мета: Вивчити рух графіків функцій:

1) Завдання вивчення літератури

2) Навчиться будувати графіки різних функцій

3) Навчиться перетворювати графіки лінійних функцій

4) Розглянути питання застосування графіків під час вирішення завдань

Об'єкт дослідження: Графіки функцій

Предмет дослідження: Руху графіків функцій

Актуальність: Побудова графіків функцій, як правило, займає дуже багато часу і вимагає уважності з боку учня, але знаючи правила перетворення графіків функцій і графіки основних функцій можна досить швидко і легко побудувати графіки функцій, що дозволить не тільки виконувати завдання на побудови графіків функцій, але і вирішувати пов'язані з ним завдання (на знаходження максимально (мінімально висоти часу та точки зустрічі))

Цей проект корисний усім учням школи.

Огляд літератури:

У літературі розглядаються способи побудови графіка різних функцій, а також наведені приклади перетворення графіків цих функцій. Графіки практично всіх основних функцій використовуються в різних технічних процесах, що дозволяє наочно уявити перебіг процесу і спрограмувати результат

Постійна функція. Ця функція задана формулою у = b де b – деяке число. Графіком постійної функції є пряма, паралельна осі абсцис і проходить через точку (0; b) осі ординат. Графіком функції у = 0 є вісь абсцис.

Види функції 1 Пряма пропорційність. Ця функція задана формулою у = kx де коефіцієнт пропорційності k ≠ 0. Графіком прямої пропорційності є пряма, що проходить через початок координат.

Лінійна функція. Така функція задана формулою у = kx + b, де k та b – дійсні числа. Графік лінійної функції є пряма.

Графіки лінійних функцій можуть перетинатися чи бути паралельними.

Так, прямі графіки лінійних функцій у = k 1 x + b 1 і у = k 2 x + b 2 перетинаються, якщо k 1 ≠ k 2 ; якщо ж k 1 = k 2 то прямі паралельні.

2Зворотна пропорційність – це функція, задана формулою у = k/x, де k ≠ 0. K називається коефіцієнтом зворотної пропорційності. Графіком зворотної пропорційності є гіпербола.

Функція у = х 2 представлена ​​графіком, який отримав назву парабола: на проміжку [-~; 0] функція зменшується, на проміжку функція зростає.

Функція у = х 3 зростає на всій числовій прямій та графічно представлена ​​кубічною параболою.

Ступінна функція з натуральним показником. Ця функція задана формулою у = х n, де n - натуральне число. Графіки статечної функції з натуральним показником залежить від n. Наприклад, якщо n = 1, графіком буде пряма (у = х), якщо n = 2, то графіком буде парабола і т.д.

Ступенева функція з негативним показником представлена ​​формулою у = х -n , де n – натуральне число. Ця функція визначена за всіх х ≠ 0. Графік функції також залежить від показника ступеня n.

Ступінна функція з позитивним дрібним показником. Ця функція представлена ​​формулою у = х r , де r - Позитивний нескоротний дріб. Ця функція також не є ні парною, ні непарною.

Графік-лінія яка відображає взаємозв'язок залежної та незалежної змінних на координатній площині. Графік служить для наочного відображення цих елементів

Незалежна змінна це змінна яка може приймати будь-які значення в області визначення функцій (де ця функція має сенс (не можна ділити на нуль))

Щоб побудувати графік функцій, необхідно

1) Знайти ОДЗ (область допустимих значень)

2) взяти кілька довільних значень для незалежної змінної

3) Знайти значення залежної змінної

4) Побудувати координатну площину відзначити на ній дані точки

5) З'єднати їх лінії за потреби дослідити отриманий графік Перетворення графіків елементарних функцій.

Перетворення графіків

У чистому вигляді основні елементарні функції трапляються, на жаль, не так часто. Набагато частіше доводиться мати справу з елементарними функціями, отриманими з основних елементарних за допомогою додавання констант та коефіцієнтів. Графіки таких функцій можна будувати, застосовуючи геометричні перетворення графіків відповідних основних елементарних функцій (чи переходити до нової системи координат). Наприклад, квадратична функція формула є квадратичну параболу формула, стиснуту втричі щодо осі ординат, симетрично відображену щодо осі абсцис, зсунуту проти напрямку цієї осі на 2/3 одиниці і зсунуту в напрямку осі ординат на 2 одиниці.

Давайте розберемося у цих геометричних перетвореннях графіка функції покроково на конкретних прикладах.

За допомогою геометричних перетворень графіка функції f(x) може бути побудований графік будь-якої функції виду формула, де формула - коефіцієнти стиснення або розтягування вздовж осей oy та ox відповідно, знаки «мінус» перед коефіцієнтами формула та формула вказують на симетричне відображення графіка щодо координатних осей , а і b визначають зсув щодо осей абсцис та ординат відповідно.

Таким чином, розрізняють три види геометричних перетворень графіка функції:

Перший вид - масштабування (стиснення або розтягнення) вздовж осей абсцис та ординат.

На необхідність масштабування вказують коефіцієнти формули відмінні від одиниці, якщо число менше 1, то відбувається стиснення графіка щодо oy і розтягнення щодо ox, якщо число більше 1, то робимо розтягнення вздовж осі ординат і стиск уздовж осі абсцис.

Другий вид – симетричне (дзеркальне) відображення щодо координатних осей.

На необхідність цього перетворення вказують знаки мінус перед коефіцієнтами формули (у цьому випадку симетрично відображаємо графік щодо осі ox) і формула (у цьому випадку симетрично відображаємо графік щодо осі oy). Якщо знаків «мінус» немає, цей крок пропускається.

Паралельне перенесення.

ПЕРЕНОС ВДОЛІ ОСІ ОРДИНАТ

f(x) => f(x) - b
Нехай потрібно збудувати графік функції у = f(х) - b. Неважко помітити, що ординати цього графіка всім значень x на |b| одиниць менше відповідних ординат графіка функцій у = f(х) при b>0 і |b| одиниць більше - при b 0 або нагору при b Для побудови графіка функції y + b = f(x) слід побудувати графік функції y = f(x) і перенести вісь абсцис на | b | одиниць вгору при b>0 чи |b| одиниць вниз у b

ПЕРЕНОС ВДОЛІ ОСІ АБСЦІСС

f(x) => f(x + a)
Нехай потрібно збудувати графік функції у = f(x + a). Розглянемо функцію y = f(x), яка у певній точці x = x1 набуває значення у1 = f(x1). Вочевидь, функція у = f(x + a) прийме таке значення в точці x2, координата якої визначається рівності x2 + a = x1, тобто. x2 = x1 - a, причому розглянута рівність справедливо для сукупності всіх значень з області визначення функції. Отже, графік функції у = f(x + a) може бути отриманий паралельним переміщенням графіка функції y = f(x) вздовж осі абсцис вліво |a| одиниць при a > 0 чи праворуч |a| одиниць при a Для побудови графіка функції y = f(x + a) слід побудувати графік функції y = f(x) і перенести вісь ординат на | одиниць вправо при a>0 чи |a| одиниць ліворуч у a

Приклади:

1.y=f(x+a)

2.y=f(x)+b

Відображення.

ПОБУДУВАННЯ ГРАФІКА ФУНКЦІЇ ВИДУ Y = F(-X)

f(x) => f(-x)
Очевидно, що функції y = f(-x) та y = f(x) приймають рівні значення в точках, абсциси яких рівні за абсолютною величиною, але протилежні за знаком. Інакше висловлюючись, ординати графіка функції y = f(-x) у сфері позитивних (негативних) значень х дорівнюватимуть ординатам графіка функції y = f(x) при відповідних за абсолютною величиною негативних (позитивних) значеннях х. Отже, отримуємо таке правило.
Для побудови графіка функції y = f(-x) слід побудувати графік функції y = f(x) та відобразити його щодо осі ординат. Отриманий графік є графіком функції y = f(-x)

ПОБУДУВАННЯ ГРАФІКА ФУНКЦІЇ ВИДУ Y = - F(X)

f(x) => - f(x)
Ординати графіка функції y = - f(x) при всіх значеннях аргументу дорівнюють абсолютної величини, але протилежні за знаком ординатам графіка функції y = f(x) при тих же значеннях аргументу. Отже, отримуємо таке правило.
Для побудови графіка функції y = f (x) слід побудувати графік функції y = f (x) і відобразити його щодо осі абсцис.

Приклади:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Деформація.

ДЕФОРМАЦІЯ ГРАФІКА ВДОЛІ ОСІ ОРДИНАТ

f(x) => k f(x)
Розглянемо функцію виду y = k f(x), де k > 0. Неважко помітити, що при рівних значеннях аргументу ординати графіка цієї функції будуть у k разів більшими за ординат графіка функції у = f(x) при k > 1 або 1/k разів менше ординат графіка функції y = f(x) при k Для побудови графіка функції y = k f(x) слід побудувати графік функції y = f(x) і збільшити його ординати в k разів при k > 1(виконати розтягнення графіка вздовж осі ординат ) або зменшити його ординати в 1/k разів при k
k > 1- Розтяг від осі Ох
0 - стиск до осі OX

ДЕФОРМАЦІЯ ГРАФІКА ВДОЛІ ОСІ АБСЦІСС

f(x) => f(k x)
Нехай потрібно побудувати графік функції y = f(kx), де k>0. Розглянемо функцію y = f(x), яка у довільній точці x = x1 набуває значення y1 = f(x1). Очевидно, що функція y = f(kx) приймає таке ж значення в точці x = x2, координата якої визначається рівністю x1 = kx2, причому ця рівність справедлива для сукупності всіх значень х з області визначення функції. Отже, графік функції y = f(kx) виявляється стислим (при k 1) вздовж осі абсцис щодо графіка функції y = f(x). Отже, отримуємо правило.
Для побудови графіка функції y = f(kx) слід побудувати графік функції y = f(x) і зменшити його абсциси в k раз при k>1 (виконати стиснення графіка вздовж осі абсцис) або збільшити його абсциси в 1/k раз при k
k > 1- Стиснення до осі Оу
0 - розтяг від осі OY