Просто про складне: комплексні числа. Звідки є пішло комплексне число

• Будемо ґрунтуватися на зв'язках, а не на механічних формулах.
• Розглянемо комплексні числа як доповнення до нашої системи числення, так само, як нуль, дробові чи негативні числа.
• Візуалізуємо ідеї у графіках, щоб краще зрозуміти суть, а не просто викладемо сухим текстом.

І наша таємна зброя: вивчення за аналогією. Ми дістанемося до комплексних чисел, почавши з їхніх предків, негативних чисел. Ось вам невеликий посібник:

Поки що сенсу в цій таблиці мало, але нехай вона буде поряд. До кінця статті все стане на свої місця.

Давайте справді зрозуміємо, що таке негативні числа

Негативні числа негаразд прості. Уявіть, що ви – європейський математик у XVIII столітті. У вас є 3 та 4, і ви можете написати 4 – 3 = 1. Все просто.

Але скільки буде 3-4? Що, власне, це означає? Як можна відібрати 4 корови від 3? Як можна мати менше ніж нічого?

Негативні числа розглядалися як повна нісенітниця, щось, що «кидало тінь на всю теорію рівнянь» (Френсіс Масерес, 1759). Сьогодні було б повною нісенітницею думати про негативні числа, як про щось нелогічне і некорисне. Запитайте вашого вчителя, чи порушують негативні числа основ математики.

Що сталося? Ми винайшли теоретичне число, яке мало корисні властивості. Негативні числа не можна торкнутися чи відчути, але вони добре описують певні зв'язки (як заборгованість, наприклад). Це дуже корисна вигадка.

Замість того, щоб сказати "Я повинен вам 30", і читати слова, щоб зрозуміти в плюсі ​​я або в мінусі, я можу просто записати "-30" і знати, що це означає. Якщо я зароблю гроші і сплачую свої борги (-30 + 100 = 70), я зможу легко записати цю транзакцію кількома символами. В мене залишиться +70.

Знаки плюсу та мінуса автоматично фіксують напрямок - вам не потрібна ціла пропозиція, щоб описати зміни після кожної транзакції. Математика стала простішою, елегантнішою. Стало не важливо, чи є негативні числа «відчутними» - у них є корисні властивості, і ми користувалися ними, поки вони міцно не увійшли до нашого побуту. Якщо хтось із ваших знайомих ще не зрозумів суть негативних чисел, тепер ви йому допоможете.

Але не принижуватимемо людські страждання: негативні числа були справжнім зрушенням у свідомості. Навіть Ейлер, геній, який відкрив число е і багато чого, не розумів негативні числа так само добре, як ми сьогодні. Вони розглядалися як «безглузді» результати обчислень.

Дивно вимагати від дітей, щоб вони спокійно розуміли ідеї, які колись бентежили навіть найкращих математиків.

Введення уявних чисел

З уявними числами та сама історія. Ми можемо вирішувати рівняння на кшталт цього цілими днями:

Відповідями будуть 3 та -3. Але припустимо, що якийсь розумник приписав сюди мінус:

Ну і ну. Таке питання змушує людей скуштувати, вперше бачачи його. Ви хочете обчислити квадратний корінь із числа, меншого, ніж нуль? Це немислимо! (Історично реально існували подібні питання, але мені зручніше представляти якогось безликого розумника, щоб не вганяти у фарбу вчених минулого).

Виглядає шалено, як свого часу виглядали і негативні числа, нуль та ірраціональні числа (неповторювані числа). У цьому питанні немає «реального» сенсу, правда?

Ні, правда. Так звані «уявні числа» нормальні так само, як і всі інші (або настільки ж ненормальні): вони є інструментом для опису світу. У тому ж дусі, як ми уявляємо, що -1, 0.3 і 0 «існують», припустимо, що існує деяке число i, де:

Іншими словами, ви множите i на себе ж, щоб одержати -1. Що зараз відбувається?

Ну, спочатку у нас, звичайно, болить голова. Але, граючи в гру «Давайте уявимо, що i існує», ми справді робимо математику простішою та елегантнішою. З'являються нові зв'язки, які ми легко можемо описати.

Ви не повірите в i, як і ті старі математики-бурчуни не вірили у існування -1. Все нові, повертають мозок у трубочку поняття складні сприйняття, та його сенс вимальовується відразу, навіть геніального Эйлера. Але, як показали нам негативні числа, нові дивні ідеї можуть бути надзвичайно корисними.

Я не люблю сам термін "уявні числа" - таке почуття, що він був обраний спеціально, щоб образити почуття i. Число і таке ж нормальне, як і інші, але за ним закріпилася прізвисько «уявне», тож ми теж будемо їй користуватися.

Візуальне розуміння негативних та комплексних чисел

Рівняння x^2 = 9 насправді означає таке:

Яке перетворення x, що застосовується двічі, перетворює 1 на 9?

Є дві відповіді: "x = 3" і "x = -3". Тобто, ви можете "масштабувати в" 3 рази або "масштабувати в 3 рази і перевернути" (перевертання або взяття зворотного результату - все це інтерпретація множення на негативну одиницю).

А тепер подумаємо про рівняння x^2 = -1, яке можна записати так:

Яке перетворення x, що застосовується двічі, перетворює 1 на -1? Хм.

• Ми не можемо помножити двічі позитивне число, тому що результат буде позитивним.
• Ми не можемо помножити двічі від'ємне число, тому що результат знову буде позитивним.

А як щодо… обертання! Звучить, звичайно, незвичайно, але якщо представити х як «поворот 90 градусів», тоді застосувавши х двічі, ми зробимо поворот на 180 градусів на координатній осі, і 1 обернеться в -1!

Ось це так! І якщо ми ще трохи над цим поміркуємо, то ми можемо зробити два обороти в протилежному напрямку, а також перейти з 1 на -1. Це "негативне" обертання або множення на -i:

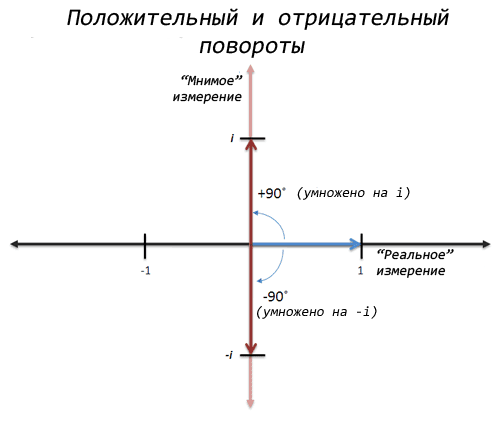
Якщо ми двічі помножимо на i, то при першому множенні отримаємо -i з 1, а при другому -1 з -i. Так що насправді існує два квадратні корені -1: i та -i.

Це досить круто! У нас є щось подібне до рішення, але що воно означає?

• i - це "нова уявна розмірність" для вимірювання числа
• i (або -i) - це те, чим «стають» числа при обертанні
• Помноження на i - це обертання на 90 градусів проти годинникової стрілки
• Множення на -i - це обертання на 90 градусів за годинниковою стрілкою.
• Подвійне обертання у кожному напрямі дає -1: воно знову повертає нас до «звичайної» розмірності позитивних і негативних чисел (вісь x).

Усі числа 2-мірні. Так, це важко прийняти, але древнім римлянам було б також важко прийняти десяткові дроби чи розподіл у стовпчик. (Як це так, між 1 та 2 є ще числа?). Виглядає дивно, як будь-який новий спосіб мислити в математиці.

Ми запитали «Як перетворити 1 на -1 на дві дії?» та знайшли відповідь: повернути 1 на 90 градусів двічі. Досить дивний новий спосіб мислити в математиці. Але дуже корисний. (Між іншим, ця геометрична інтерпретація комплексних чисел з'явилася тільки через десятиліття після відкриття самого числа i).

Також, не забувайте, що прийняття обороту проти годинникової стрілки за позитивний результат - це суто людська умовність і все могло б бути зовсім по-іншому.

Пошук множин

Давайте трохи заглибимося в деталі. При множенні негативних чисел (як -1) ви отримуєте безліч:

• 1, -1, 1, -1, 1, -1, 1, -1

Оскільки -1 не змінює розмір числа, а лише знак, ви отримуєте одне й те число то зі знаком «+», то зі знаком «-». Для числа х у вас вийде:

• x, -x, x, -x, x, -x…

Це дуже корисна думка. Число «х» може представляти хороші та погані тижні. Уявімо, що гарний тиждень змінює поганий; це гарний тиждень; а який буде 47-й тиждень?

X означає, що тиждень видасться поганим. Бачите, як негативні числа «стежать за знаком» - ми можемо просто ввести (-1)^47 в калькуляторі замість того, щоб рахувати («Тиждень 1 хороший, тиждень 2 поганий… тиждень 3 хороший…»). Речі, які постійно чергуються, можна добре змоделювати, використовуючи негативні числа.

Добре, що буде, якщо ми продовжимо множити на i?

Дуже смішно, давайте трохи це все спростимо:

Ось те саме представлено графічно:

Ми повторюємо цикл кожен 4-й поворот. У цьому безперечно є сенс, так? Будь-яка дитина скаже вам, що 4 повороти вліво – це все одно, що не повертатися зовсім. А тепер відірвіться від уявних чисел (i, i^2) і подивіться на загальну множину:

• X, Y, -X, -Y, X, Y, -X, -Y…

Як негативні числа моделюють дзеркальне відображення чисел, уявні числа можуть моделювати будь-що, що обертається між двома вимірами «Х» і «Y». Чи що завгодно з циклічною, круговою залежністю – є щось на прикметі?

Розуміння комплексних чисел

Є ще одна деталь для розгляду: чи може бути число і «реальним», і «уявним»?

Навіть не сумнівайтесь. Хто сказав, що нам обов'язково треба повертати на 90 градусів? Якщо ми однією ногою станемо на «реальну» розмірність, а іншою – на «уявну», то виглядатиме приблизно так:

Ми знаходимося на позначці в 45 градусів, де речова та уявна частини однакові, і саме число дорівнює «1+i». Це як хот-дог, де є і кетчуп, і гірчиця – хто сказав, що треба обов'язково обирати щось одне?

По суті, ми можемо вибрати будь-яку комбінацію речовинної та уявної частини і зробити з цього трикутник. Кут стає «кутом обертання». Комплексне число - це химерна назва для чисел, в яких є речова і уявна частини. Вони пишуться, як a + bi, де:

• a - речова частина
• b - уявна частина

Не погано. Але залишається одне останнє питання: як «велико» комплексне число? Ми не можемо виміряти речову частину або уявну окремо, тому що ми пропустимо загальну картину.

Давайте зробимо крок назад. Розмір від'ємного числа - це відстань від нуля:

Це інший спосіб знайти абсолютну величину. Але як виміряти обидва компоненти на 90 градусах для комплексних чисел?

Це птах у небі… чи літак… Піфагор поспішає на допомогу!

Ця теорема вискакує, де тільки можна, навіть у числах, вигаданих через 2000 років після самої теореми. Так, ми робимо трикутник, і його гіпотенуза і дорівнюватиме відстані від нуля:

Хоча виміряти комплексне число не так просто, як «просто опустити знак -», комплексні числа мають дуже корисні застосування. Давайте розглянемо деякі з них.

Реальний приклад: обертання

Ми не чекатимемо університетського курсу фізики, щоб попрактикуватися з комплексними числами. Ми займемося цим уже сьогодні. Багато можна розповісти на тему множення комплексних чисел, але поки що потрібно зрозуміти головне:

• Множення на комплексне число здійснює обертання на його кут

Погляньмо, як це працює. Уявіть, що я на човні, рухаюся з курсом 3 одиниці на Схід кожні 4 одиниці на Північ. Я хочу змінити свій курс на 45 градусів проти годинникової стрілки. Яким буде новий курс?

Хтось може сказати: «Це просто! Обчисліть синус, косинус, погуглите значення за тангенсом…і тоді…» Здається, я зламав свій калькулятор…

Давайте підемо більш простим шляхом: ми йдемо курсом 3 + 4i (не важливо, який тут кут, нам все одно поки) і хочемо повернутися на 45 градусів. Ну, 45 градусів це 1+i (ідеальна діагональ). Тож ми можемо помножити наш курс на це число!

Ось у чому суть:

• Вихідний курс: 3 одиниці на Схід, 4 одиниці на Північ = 3+4i
• Обертання проти годинникової стрілки на 45 градусів = множення на 1 + i

При множенні ми отримуємо:

Наш новий орієнтир – 1 одиниця на Захід (-1 на Схід) та 7 одиниць на Північ, можете намалювати координати на графіку та дотримуватися їх.

Але! Ми знайшли відповідь за 10 секунд, без жодних синусів та косинусів. Не було векторів, матриць, відстеження, в якому квадранті ми знаходимося. Це була проста арифметика та трохи алгебри для приведення рівняння. Уявні числа чудово справляються з обертанням!

Більше того, результат такого обчислення дуже корисний. У нас є курс (-1, 7) замість кута (atan(7/-1) = 98.13, і відразу зрозуміло, що ми в другому квадранті. Як, власне, ви планували намалювати і слідувати вказаному куту? Використовуючи транспортир під рукою?

Ні, ви конвертували б кут в косинус і синус (-0.14 і 0.99), знайшли б зразкове співвідношення між ними (близько 1 до 7) і накидали б трикутник. І тут комплексні числа безперечно виграють - акуратно, блискавично, і без калькулятора!

Якщо ви схожі на мене, то це відкриття здасться вам надзвичайним. Якщо ні, боюся, що математика вас не запалює. Вибачте!

Тригонометрія хороша, але комплексні числа значно спрощують обчислення (на зразок пошуку cos(a + b)). Це лише невеликий анонс; у наступних статтях я надам вам повне меню.

Ліричний відступ: деякі люди думають приблизно так: «Гей, ну не зручно ж мати курс Північ/Схід замість простого кута для прямування судна!»

Правда? Ну гаразд, подивіться на свою праву руку. Який кут між основою вашого мізинця та кінчиком вказівного пальця? Успіхів з вашим способом обчислення.

А можна просто відповісти "Ну, кінчик знаходиться на Х дюймів вправо і Y дюймів вгору" і з цим вже можна щось зробити.

Комплексні числа стали ближчими?

Ми пронеслися смерчем моїми базовими відкриттями в області комплексних чисел. Подивіться на першу ілюстрацію, тепер він має стати зрозумілішим.

Є ще стільки всього цікавого в цих гарних, чудових числах, але мій мозок уже втомився. Моя мета була проста:

• Переконати вас у тому, що комплексні числа лише розглядалися як «божевілля», а насправді вони можуть бути дуже корисними (як і негативні числа)
• Показати, як комплексні числа можуть спростити деякі завдання на кшталт обертання.

Якщо я здається занадто стурбованим цією темою, то для цього є причина. Уявні числа роками були моєю нав'язливою ідеєю - недолік розуміння мене дратував.

Але запалити свічку краще, ніж пробиратися крізь темряву: ось мої думки, і я впевнений, що вогник запалиться і в умах моїх читачів.

Епілог: Але вони, як і раніше, досить дивні!

Я знаю, вони і для мене все ще дивні. Я намагаюся думати, як думав перший чоловік, який відкрив нуль.

Нуль - це така дивна ідея, "щось" представляє "нічого", і це ніяк не могли зрозуміти в Стародавньому Римі. Те саме і з комплексними числами - це новий спосіб мислення. Але й нуль, і комплексні числа значно спрощують математику. Якби ми ніколи не впроваджували дива на зразок нових систем числення, ми б досі вважали все на пальцях.

Я повторюю цю аналогію, тому що так легко почати думати, що комплексні числа є «не нормальними». Давайте бути відкритими до нововведень: у майбутньому люди лише жартуватимуть з того, як хтось аж до XXI століття не вірив у комплексні числа.

Комплексні числа для чайників. Урок 1. Що це таке та з чим їх "їдять". Уявна одиниця.

Щоб зрозуміти, що таке комплексні числа, давайте згадаємо про звичайні числа і всебічно їх розглянемо. І так, найпростіше - це натуральнічисла. Вони називаються натуральними, тому що через них можна щось висловити "в натурі", тобто, щось порахувати. Ось є два яблука. Їх можна порахувати. Є п'ять коробок цукерок. Їх можна порахувати. Інакше кажучи, натуральні числа - це числа, з яких ми можемо вважати конкретні предмети. Ви чудово знаєте, що ці числа можна складати, віднімати, множити та ділити. Зі складанням і множенням все зрозуміло. Було два яблука, додали три, стало п'ять. Взяли три коробки цукерок по 10 штук у кожній, отже, всього тридцять цукерок. А ось тепер перейдемо до цілимчислам. Якщо натуральні числа позначають конкретну кількість предметів, то безліч цілих чисел вводяться абстракції. Це нульі негативнічисла. Чому це абстракції? Нуль - це відсутність чогось. Але чи можемо ми помацати, помацати те, чого немає. Ось два яблука ми можемо помацати, ось вони. Ми можемо їх навіть з'їсти. А що означає нуль яблук? Ми можемо помацати, помацати цей нуль? Ні, не можемо. Значить, це абстракція. Треба ж якось позначати відсутність чогось. Ось і позначили цифрою нуль. Але навіщо це якось позначати? Уявімо, що у нас було два яблука. Ми з'їли два. Скільки у нас лишилося? Правильно, анітрохи. Цю операцію (з'їли два яблука) ми запишемо як віднімання 2-2. І що в результаті щось у нас полупилося? Як нам визначити результат? Тільки ввівши нову абстракцію (нуль), яка означать, що в результаті віднімання (з'їдання) вийшло, що в нас не залишилося жодного яблука. Але ми з двох можемо відняти не 2, а 3. Здавалося б, ця операція безглузда. Якщо у нас лише два яблука, як ми зможемо з'їсти три?

Розглянемо інший приклад. Ми йдемо до магазину за пивом. У нас із собою 100 рублів. Пиво коштує 60 рублів за пляшку. Ми хочемо купити дві пляшки, але грошей у нас не вистачає. Нам треба 120 рублів. І тут ми зустрічаємо свого давнього приятеля та займаємо у нього двадцятку. Купуємо пиво. Запитання. Скільки у нас лишилося грошей? Здоровий глузд підказує, що анітрохи. Але з погляду математики це буде абсурдом. Чому? Тому що для того, щоб отримати в результаті нуль, потрібно зі 100 відібрати 100. А ми робимо 100-120. Тут у нас має вийти щось інше. А що в нас вийшло? А те, що ми ще маємо приятелю 20 рублів. Наступного разу, коли ми матимемо з собою 140 рублів, ми прийдемо в магазин за пивом, зустрінемо приятеля, розрахуємося з ним за боргами і зможемо купити ще дві пляшки пива. У результаті виходить 140-120-20=0. Зверніть увагу на -20. Це чергова абстракція. від'ємне число. Тобто наш обов'язок перед приятелем - це число зі знаком мінус, тому що коли ми борг віддаємо, ми цю суму віднімаємо. Скажу більше, це ще більша абстракція, ніж нуль. Нуль позначать щось, чого немає. А негативне число - це як би те, що в нас буде відібрано в майбутньому.

Отже, на прикладі я показав, як у математиці народжуються абстракції. І, що, здавалося б, при всій безглуздості подібних абстракцій (типу відібрати більше, ніж було), вони знаходять застосування в реальному житті. У разі поділу цілих чисел виникає ще одна абстракція - дробові числа.На них я докладно зупинятись не будуть, і так зрозуміло, що вони потрібні в тому випадку, коли у нас цілі числа не діляться на ціле. Наприклад, у нас чотири яблука, а треба їх поділити на троє людей. Тут зрозуміло, що одне яблуко, що залишилося, ділимо на три частини і отримуємо дроби.

Тепер дуже так плавно дістанемося до самих комплексних чисел. Але, спочатку згадаємо, що з множенні двох негативних числі виходить позитивне. Хтось запитати – а чому так? Спершу розберемося з множенням негативного числа на позитивне. Допустимо, -20 множимо на 2. Тобто нам треба скласти -20+-20. Через війну виходить -40, оскільки збільшення негативного числа - це віднімання. Чому віднімання - див. вище, негативне число - це борг, коли ми заберемо його в нас щось віднімається. Є й інший життєвий зміст. Що буде, якщо борг збільшився? Наприклад, у тому випадку, коли нам дали у борг під відсотки? У результаті залишилося теж число зі знаком мінус, те, що після мінуса побільшало. А що означає помножити на від'ємне число? Що означає 3*-2? Це означає, що число три потрібно взяти мінус двічі. Тобто поставити мінус перед результатом множення. До речі, це те саме, що -3*2, тому що від перестановки множників твір не змінюється. А тепер увага. Помножуємо -3 на -2. Ми число -3 беремо мінус двічі. Якщо ми візьмемо число -3 двічі, то буде -6, це ви зрозуміли. А якщо взяти мінус двічі? Але що означає мінус взяти мінус разів? Якщо взяти позитивне число мінус разів, то в результаті вийти негативне, у нього змінюється символ. Якщо ми негативне число беремо мінус разів, то у нього змінюється знак і воно стає позитивним.

Навіщо ми міркували про множення мінус на мінус? А для того, щоб розглянути ще одну абстракцію, цього разу вона має безпосереднє відношення до комплексних чисел. Це уявна одиниця. Уявна одиниця дорівнює квадратному кореню з мінус 1:

Нагадаю, що таке квадратне коріння. Це операція, обернена до зведення в квадрат. А зведення в квадрат – це множення числа саме на себе. Таким чином, квадратний корінь із 4 дорівнює 2, тому що 2*2=4. Квадратний корінь із 9 - це 3, оскільки 3*3=9. Квадратний корінь із одиниці так само виходить одиниця, з нуля нуль. Але як нам витягти квадратний корінь із мінус одиниці? Яке число треба помножити на себе, щоб отримати -1? А немає такої кількості! Якщо ми помножимо -1 саму себе, то в результаті отримаємо 1. Якщо 1 помножимо на 1, то отримаємо 1. А мінус -1 ми таким чином ніяк не отримаємо. Проте ми можемо зіткнутися з ситуацією, коли під коренем виявиться негативне число. Що ж робити? Можна, звичайно, сказати, що рішення немає. Це як при розподілі на нуль. Всі ми до якогось часу вважали, що на нуль ділити не можна. Але потім дізналися про таку абстракцію, як нескінченність, і виявилося, що ділити на нуль все ж таки можна. Більш того, такі абстракції, як розподіл на нуль, або невизначеність, що отримується при розподілі нуля на нуль або нескінченності на нескінченність, а так само інші подібні операції, широко застосовуються у вищій математиці (), а вища математика - це основа багатьох точних наук, які рухають вперед технічний прогрес. Так може і в уявній одиниці є якийсь таємний зміст? Є. І ви його зрозумієте, читаючи подальші мої уроки за комплексними числами. А поки що я розповім про деякі сфери, де комплексні числа (числа, у складі яких є уявна одиниця) застосовуються.

І так, ось перелік областей, де застосовуються комплексні числа:

Електротехніка Розрахунок ланцюгів змінного струму.Використання комплексних чисел у разі дуже полегшує розрахунок, без них довелося б застосовувати диференціальні та інтегральні рівняння.

Квантова механіка.Коротко - в квантової механіки є таке поняття як хвильова функція, яка сама по собі комплекснозначна і квадрат якої (вже дійсне число) дорівнює густині ймовірності знаходження частки в даній точці. також цикл уроків

Цифрове оброблення сигналів.Теорія цифрової обробки сигналів включає таке поняття, як z-перетворення, яке полегшує різні обчислення, зв'язкові з розрахунком характеристик різних сигналів, таких як частотна і амплітудна характеристика та інше.

Опис процесів плоского перебігу рідин.

Обтікання профілів рідиною.

Хвильові рухи рідини.

І це далеко не вичерпний список, де застосовують комплексні числа. На цьому перше знайомство із комплексними числами закінчено, до нових зустрічей.

Під час вивчення властивостей квадратного рівняння ставилося обмеження - для дискримінанта менше нуля рішення немає. Відразу обговорювалося, що йдеться про безліч дійсних чисел. Допитливий розум математика зацікавиться - який секрет міститься в застереженні про речові значення?

Згодом математики запровадили поняття комплексних чисел, де за одиницю приймається умовне значення кореня другого ступеня мінус одиниці.

Історична довідка

Математична теорія розвивається послідовно, від найпростішого до складного. Розберемося, як виникло поняття, що отримало назву "комплексне число", і навіщо воно потрібне.

З давніх-давен основу математики становив простий рахунок. Дослідникам було відоме лише натуральне безліч значень. Додавання і віднімання при цьому проводилося просто. У міру ускладнення господарських відносин замість додавання однакових значень почали застосовувати множення. З'явилася зворотна операція до множення – розподіл.

Поняття натурального числа обмежувало використання арифметичних операцій. На багатьох цілих значень неможливо вирішувати всі завдання поділу. призвела спочатку до поняття раціональних значень, а потім і до ірраціональних значень. Якщо для раціонального можна вказати точне розташування точки на лінії, то для ірраціональних таку точку вказати неможливо. Можна лише приблизно вказати інтервал знаходження. Об'єднання раціональних та ірраціональних числа утворили речову множину, яку можна представити як деяку лінію із заданим масштабом. Кожен крок по лінії – це натуральне число, а між ними розташовуються раціональні та ірраціональні значення.

Почалася доба теоретичної математики. Розвиток астрономії, механіки, фізики вимагало вирішення дедалі складніших рівнянь. У загальному вигляді було знайдено коріння квадратного рівняння. При вирішенні складнішого кубічного багаточлена вчені зіткнулися з протиріччям. Поняття кубічного кореня з негативного має сенс, а квадратного виходить невизначеність. При цьому квадратне рівняння – лише окремий випадок кубічного.

У 1545 році італієць Дж. Кардано запропонував запровадити поняття уявного числа.

Таким числом став корінь другого ступеня мінус одиниці. Остаточно термін комплексного числа сформувався лише за триста років, у роботах відомого математика Гаусса. Він запропонував формально поширити на уявне число всі закони алгебри. Речова пряма розширилася до площини. Світ став більшим.

Основні поняття

Згадаймо ряд функцій, які мають обмеження на речовому множині:

• y = arcsin(x), визначена в інтервалі значень між негативною та позитивною одиницею.
• y = ln(x) має сенс при позитивних аргументах.
• квадратний корінь y = x, розраховується тільки для x ≥ 0.

Позначенням i = √(-1), введемо таке поняття, як уявне число, це дозволить зняти всі обмеження з області визначення наведених вище функцій. Вирази типу y = arcsin(2), y = ln(-4), y = √(-5) набувають сенсу в деякому просторі комплексних чисел.

Алгебраїчну форму можна записати у вигляді виразу z = x + i x y на множині речових значень x і y, а i 2 = -1.

Нове поняття знімає всі обмеження на використання будь-якої функції алгебри і своїм виглядом нагадує графік прямий в координатах речових і уявних значень.

Комплексна площина

Геометрична форма комплексних чисел наочно дозволяє уявити багато їх властивостей. По осі Re(z) відзначаємо речові значення x, Im(z) - уявні величини y, тоді точка z на площині відображатиме необхідне комплексне значення.

Визначення:

• Re(z) – реальна вісь.
• Im(z) - означає уявну вісь.
• z – умовна точка комплексного числа.
• Чисельне значення довжини вектора від нульової точки до z називається модулем.
• Реальна та уявна осі розбивають площину на чверті. При позитивному значенні координат – І чверть. При аргументі реальної осі менше 0, а уявної більше 0 - ІІ чверть. Коли координати негативні – ІІІ чверть. Остання IV чверть містить безліч позитивних реальних значень і негативних уявних величин.

Таким чином, на площині зі значеннями координат x і y завжди можна наочно зобразити точку комплексного числа. Символ і вводиться для відокремлення реальної частини від уявної.

Властивості

1. При нульовому значенні уявного аргументу отримуємо просто число (z = x), яке розташовується на реальній осі і належить речовому множині.
2. Особливий випадок, коли значення реального аргументу стає нульовим, вираз z = i x y відповідає розташування точки на уявній осі.
3. Загальний вигляд z = x + i x y буде при ненульових значеннях аргументів. Означає розташування точки, що характеризує комплексне число, в одній із чвертей.

Тригонометричний запис

Згадаймо полярну систему координат та визначення sin та cos. Очевидно, що за допомогою цих функцій можна описати розташування будь-якої точки на площині. Для цього достатньо знати довжину полярного променя та кут нахилу до речової осі.

Визначення. Запис виду ∣z ∣, помножений на суму тригонометричних функцій cos(ϴ) та уявної частини i ×sin(ϴ), називається тригонометричним комплексним числом. Тут застосовується позначення кут нахилу до речової осі

ϴ = arg(z), а r = ∣z∣, довжина променя.

З визначення та властивостей тригонометричних функцій випливає дуже важлива формула Муавра:

z n = r n × (cos (n × ϴ) + i × sin (n × ϴ)).

Використовуючи цю формулу, зручно вирішувати багато систем рівнянь, що містять тригонометричні функції. Особливо коли виникає завдання зведення у ступінь.

Модуль та фаза

Для завершення опису комплексної множини запропонуємо два важливі визначення.

Знаючи теорему Піфагора, легко вирахувати довжину променя в полярній системі координат.

r = ∣z∣ = √(x 2 + y 2), такий запис на комплексному просторі має назву "модуль" і характеризує відстань від 0 до точки на площині.

Кут нахилу комплексного променя до речовинної прямої прийнято називати фазою.

З визначення видно, що реальна та уявна частини описуються за допомогою циклічних функцій. А саме:

• x = r × cos(ϴ);
• y = r × sin(ϴ);

Назад, фаза має зв'язок з значеннями алгебри через формулу:

ϴ = arctan(x / y) + µ, поправка µ вводиться для врахування періодичності геометричних функцій.

Формула Ейлера

Математики часто використовують показову форму. Числа комплексної площини записують у вигляді виразу

z = r × e i × ϴ, яка випливає із формули Ейлера.

Такий запис набула широкого поширення для практичного обчислення фізичних величин. Форма подання у вигляді показових комплексних чисел особливо зручна для інженерних розрахунків, де виникає необхідність розрахувати ланцюги із синусоїдальними струмами та необхідно знати значення інтегралів функцій із заданим періодом. Самі розрахунки є інструментом при конструюванні різних машин і механізмів.

Визначення операцій

Як зазначалося, на комплексні числа поширюються все алгебраїчні закони роботи з основними математичними функціями.

Операція суми

При складанні комплексних значень їх реальна та уявна частини також складаються.

z = z 1 + z 2 де z 1 і z 2 - комплексні числа загального виду. Перетворюючи вираз, після розкриття дужок та спрощення запису, отримаємо реальний аргумент х = (x 1 + x 2), уявний аргумент y = (y 1 + y 2).

На графіку це виглядає як додавання двох векторів, за відомим правилом паралелограма.

Операція віднімання

Розглядається як окремий випадок додавання, коли одне число позитивне, інше негативне, тобто що знаходиться в дзеркальній чверті. Алгебраїчна запис виглядає як різницю реальних і уявних частин.

z = z 1 - z 2 або, враховуючи значення аргументів, аналогічно операції додавання, отримуємо для реальних значень х = (x 1 - x 2) і уявних y = (y 1 - y 2).

Розмноження на комплексній площині

Використовуючи правила роботи з многочленами, виведемо формулу на вирішення комплексних чисел.

Дотримуючись загальних правил алгебри z=z 1 ×z 2 , розписуємо кожен аргумент і наводимо подібні. Реальну та уявну частини можна записати так:

• х = х 1 × x 2 - y 1 × y 2
• y = x 1 x y 2 + x 2 x y 1.

Красивіше виглядає, якщо використовуватимемо показові комплексні числа.

Вираз виглядає так: z = z 1 × z 2 = r 1 × e i χ 1 × r 2 × e i ϴ 2 = r 1 × r 2 × e i (ϴ 1+ ϴ 2) .

Поділ

При розгляді операції розподілу, як зворотної до операції множення, у показовій формі запису отримуємо простий вираз. Розподіл значення z 1 на z 2 є результатом поділу їх модулів і різниці фаз. Формально при використанні показової форми комплексних чисел це виглядає так:

z = z 1 / z 2 = r 1 × e i χ 1 / r 2 × e i ϴ 2 = r 1 / r 2 × e i (χ 1-ϴ 2) .

У вигляді запису алгебри операція поділу чисел комплексної площини записується трохи складніше:

Розписуючи аргументи і проводячи перетворення багаточленів, легко отримати значення х = x 1 × x 2 + y 1 × y 2 відповідно y = x 2 × y 1 - x 1 × y 2 , правда, в рамках описуваного простору цей вислів має сенс, якщо z 2 ≠ 0.

Вилучаємо корінь

Все вищеописане можна застосовувати щодо більш складних алгебраїчних функцій - зведення будь-яку ступінь і зворотну до неї - вилучення кореня.

Користуючись загальним поняттям зведення ступінь n, отримуємо визначення:

z n = (r × e i ϴ) n .

Використовуючи загальні властивості, перепишемо у вигляді:

z n = r n × e i χ n .

Отримали просту формулу зведення до ступеня комплексного числа.

З визначення ступеня одержуємо дуже важливе слідство. Парний ступінь уявної одиниці завжди дорівнює 1. Будь-який непарний ступінь уявної одиниці завжди дорівнює -1.

Тепер вивчимо зворотну функцію – вилучення кореня.

Для простоти запису приймемо n = 2. Квадратним коренем w комплексного значення z на комплексній площині C прийнято вважати вираз z = ±, справедливе для будь-якого речового аргументу більшого або рівного нулю. При w ≤ 0 рішення не існує.

Подивимося на найпростіше квадратне рівняння z 2 = 1. Використовуючи формули комплексних чисел, перепишемо r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0 . З запису видно, що r 2 = 1 і ϴ = 0, отже, маємо єдине рішення, що дорівнює 1. Але це суперечить поняттю, що z = -1 теж відповідає визначенню квадратного кореня.

Розберемося, що ми не враховуємо. Якщо згадаємо тригонометричний запис, то відновимо твердження - при періодичній зміні фази комплексне число не змінюється. Позначимо символом p значення періоду, тоді справедливий запис r 2 × e i 2ϴ = e i (0+ p) , звідки 2ϴ = 0 + p, або ϴ = p / 2. Отже, справедливо e i 0 = 1 і e i p /2 = -1 . Отримали друге рішення, що відповідає загальному розумінню квадратного кореня.

Отже, щоб знайти довільний корінь із комплексного числа, діятимемо за процедурою.

• Запишемо показову форму w = ∣w∣ × e i (arg (w) + pk) , k - довільне ціле число.
• Шукане число теж представимо формою Ейлера z = r × e i ϴ .
• Скористаємося загальним визначенням функції вилучення кореня r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) .
• Із загальних властивостей рівності модулів та аргументів запишемо r n = ∣w∣ і nϴ = arg (w) + p×k.
• Підсумковий запис кореня з комплексного числа описується формулою z = √∣w∣ × e i (arg (w) + pk) / n.
• Зауваження. Значення ∣w∣, за визначенням, є позитивним речовим числом, отже, корінь будь-якого ступеня має сенс.

Поле та сполучення

На завершення дамо два важливі визначення, які мало значення для вирішення прикладних завдань з комплексними числами, але істотні при подальшому розвитку математичної теорії.

Кажуть, що вирази додавання та множення утворюють поле, якщо задовольняють аксіомам для будь-яких елементів комплексної площини z:

1. Від зміни місць комплексних доданків комплексна сума не змінюється.
2. Правильно твердження - у складному вираженні будь-яку суму двох чисел можна замінити з їхньої значення.
3. Існує нейтральне значення 0, котрим вірно z + 0 = 0 + z = z.
4. Для будь-якого z існує протилежність - z, додавання з яким дає нуль.
5. При зміні місць комплексних множників комплексне твір не змінюється.
6. Примноження двох будь-яких чисел можна замінити на їх значення.
7. Існує нейтральне значення 1, множення на яке змінює комплексне число.
8. Для кожного z ≠ 0 є зворотне значення z -1 , множення на яке дає в результаті 1.
9. Множення суми двох чисел на третє рівносильне операції множення кожного з них на це число та складання результатів.
10. 0 ≠ 1.

Числа z 1 = x + i x y і z 2 = x - i x y називаються сполученими.

Теорема.Для поєднання правильне твердження:

• Поєднання суми дорівнює сумі сполучених елементів.
• Поєднання твору дорівнює твору сполучення.
• дорівнює самому числу.

У загальній алгебрі такі властивості прийнято називати автоморфізмом поля.

Приклади

Дотримуючись наведених правил і формул комплексних чисел, легко можна ними оперувати.

Розглянемо найпростіші приклади.

Завдання 1.Використовуючи рівність 3y +5 x i = 15 - 7i, визначити x та y.

Рішення. Згадаймо визначення комплексних рівностей, тоді 3y = 15, 5x = -7. Отже, x = -7/5, y = 5.

Завдання 2.Обчислити значення 2 + i 28 та 1 + i 135 .

Рішення. Очевидно, 28 – парне число, з наслідку визначення комплексного числа у ступеню маємо i 28 = 1, отже, вираз 2 + i 28 = 3. Друге значення, i 135 = -1, тоді 1 + i 135 = 0.

Завдання 3.Обчислити добуток значень 2 + 5i та 4 + 3i.

Рішення. Із загальних властивостей множення комплексних чисел одержуємо (2 + 5i) Х (4 + 3i) = 8 - 15 + i (6 + 20). Нове значення буде -7+26i.

Завдання 4.Обчислити коріння рівняння z3 = -i.

Рішення. Варіантів, як знайти комплексне число, може бути кілька. Розглянемо один із можливих. За визначенням, ∣ - i∣ = 1, фаза для -i дорівнює -р/4. /3 для будь-якого цілого k.

Багато рішень має вигляд (e - ip/12 , e ip /4 , e i 2 p/3).

Навіщо потрібні комплексні числа

Історія знає безліч прикладів, коли вчені, працюючи над теорією, навіть не замислюються про практичне застосування своїх результатів. Математика - це насамперед гра розуму, жорстке дотримання причинно-наслідкових зв'язків. Майже всі математичні побудови зводяться до розв'язання інтегральних і диференціальних рівнянь, а ті, своєю чергою, з деяким наближенням, вирішуються знаходженням коріння багаточленів. Тут ми вперше зустрічаємося з парадоксом уявних чисел.

Вчені дослідники, вирішуючи цілком практичні завдання, вдаючись до рішень різних рівнянь, виявляють математичні парадокси. Інтерпретація цих парадоксів призводить до надзвичайних відкриттів. Подвійна природа електромагнітних хвиль один із таких прикладів. Комплексні числа у розумінні їх властивостей відіграють вирішальну роль.

Це, у свою чергу, знайшло практичне застосування в оптиці, радіоелектроніці, енергетиці та багатьох інших технологічних галузях. Ще один приклад, набагато важчий для розуміння фізичних явищ. Антиматерія була передбачена на кінчику пера. І лише за багато років починаються спроби її фізичного синтезування.

Не треба думати, що лише у фізиці існують такі ситуації. Не менш цікаві відкриття відбуваються в живій природі при синтезуванні макромолекул під час вивчення штучного розуму. І все це завдяки розширенню нашої свідомості, уникнення простого додавання і віднімання натуральних величин.