Раціональні рівняння - Гіпермаркет знань. Устаткування, демонстраційний матеріал

Муніципальний загальноосвітній заклад

Середня загальноосвітня школа №21

Раціональні рівняння.

(8 клас)

Вчитель математики:

Квасніцька І.В.

Килимів,

2010-2011

Тема:Раціональні рівняння.

Ціль:Формування навичок розв'язання раціональних рівнянь.

Завдання:- Формування поняття «Раціональне рівняння»;

Формування навичок розв'язання раціональних рівнянь у різний спосіб;

Вдосконалення навичок перетворення алгебраїчних дробів;

Удосконалення навичок застосування формул скороченого множення у перетворенні алгебраїчних дробів;

Вдосконалення навичок усного рахунку;

Розвиток розумових операцій;

Виховання грамотного математичного мовлення, акуратності;

Виховання співробітництва, взаємодопомоги.

План уроку:

1. Самовизначення до навчальної діяльності.

2. Актуалізація знань та фіксація утруднення в діяльності.

3. Виявлення причини утруднення та постановка мети діяльності.

4. Побудова проекту виходу із скрути.

5. Первинне закріплення у зовнішній промови.

6. Самостійна робота з самоперевіркою за зразком.

7. Включення в систему знань та повторення.

8. Рефлексія діяльності під час уроку.

9. Домашнє завдання.

Хід уроку.

Обладнання, демонстраційний матеріал:

1) завдання для актуалізації знань

№ 1 · ·

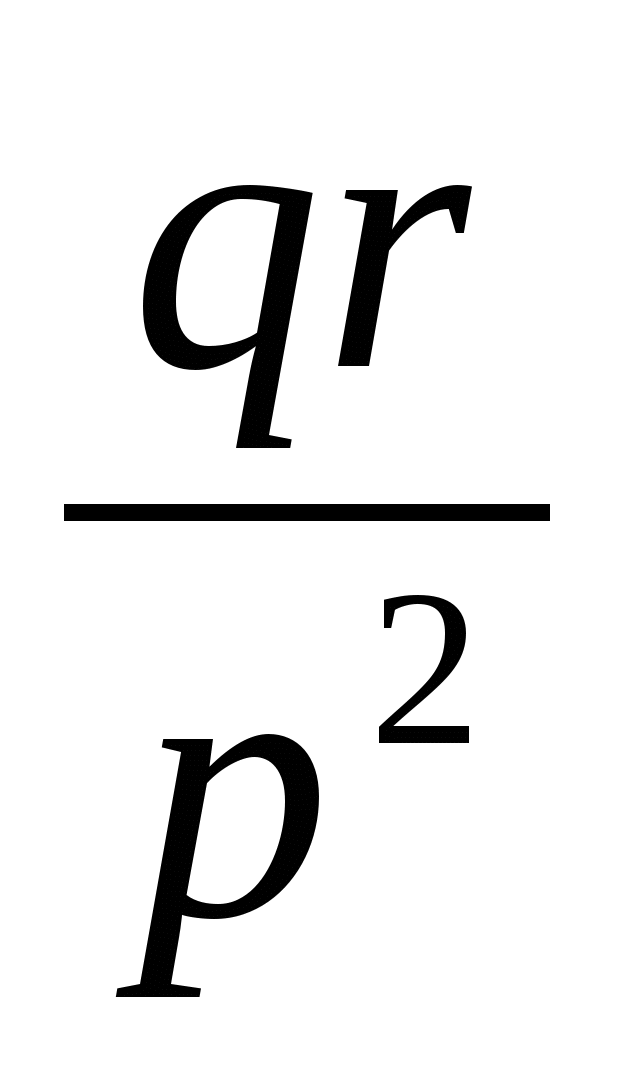№2
+
:
-

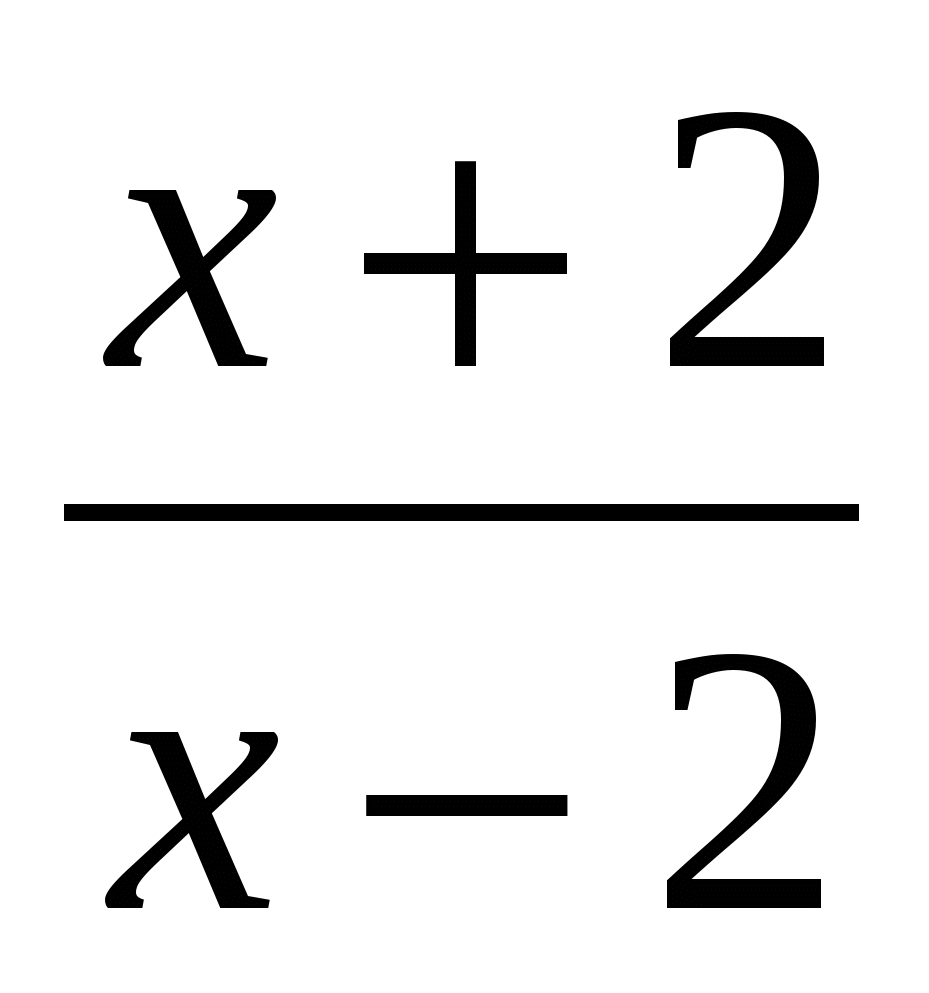
№ 3
-2х =
+

№ 4
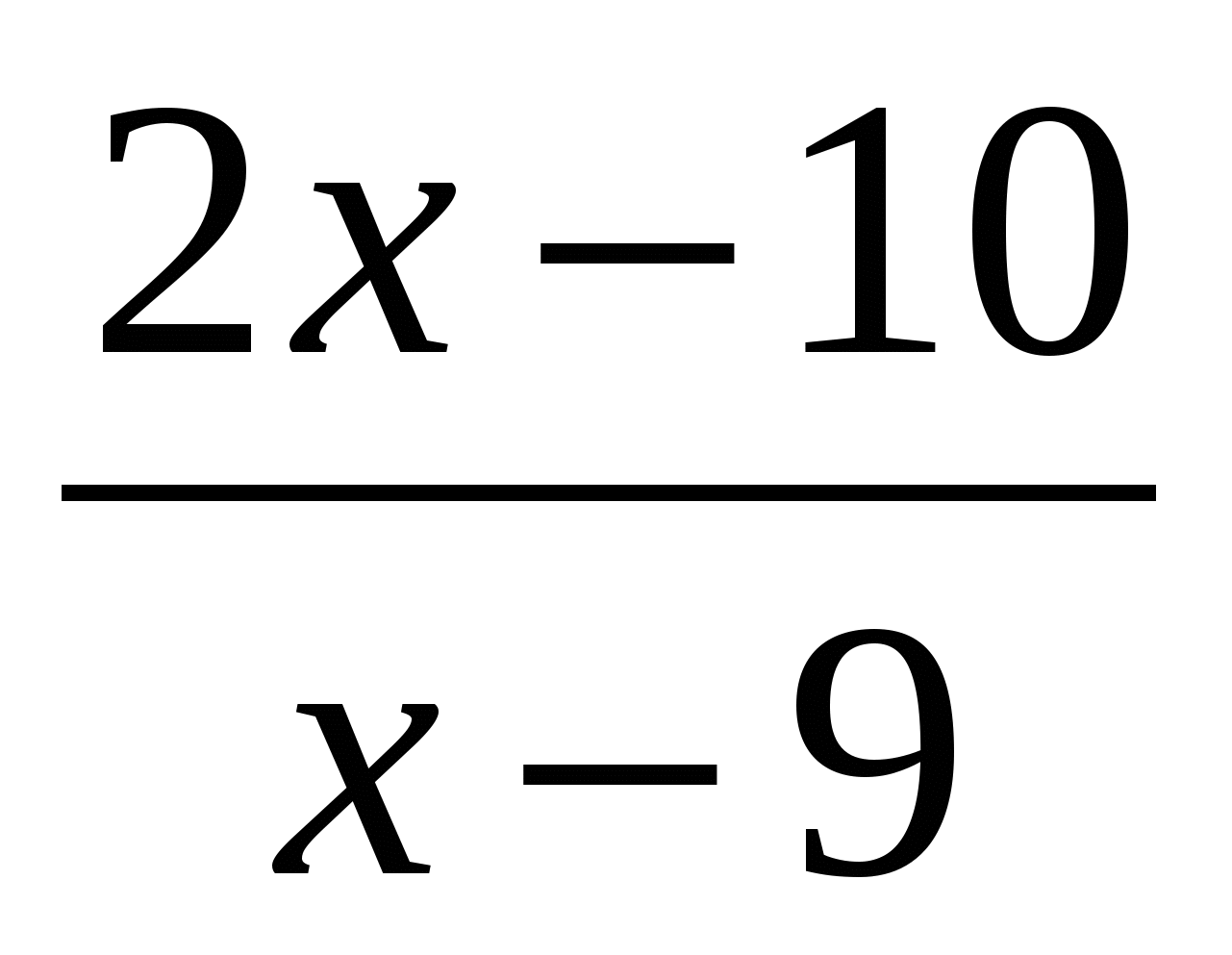=0.

2) Алгоритм розв'язання рівнянь

1) Привести дроби до спільного знаменника у лівій та правій частинах рівняння.

2) Скористатися правилами:

а) рівності дробу нулю;

б) властивостями пропорції;

в) рівності дробів.

3) Алгоритм розв'язання раціональних рівнянь

4) Завдання для первинного закріплення у зовнішній промові

-
=
,

-
=,

+
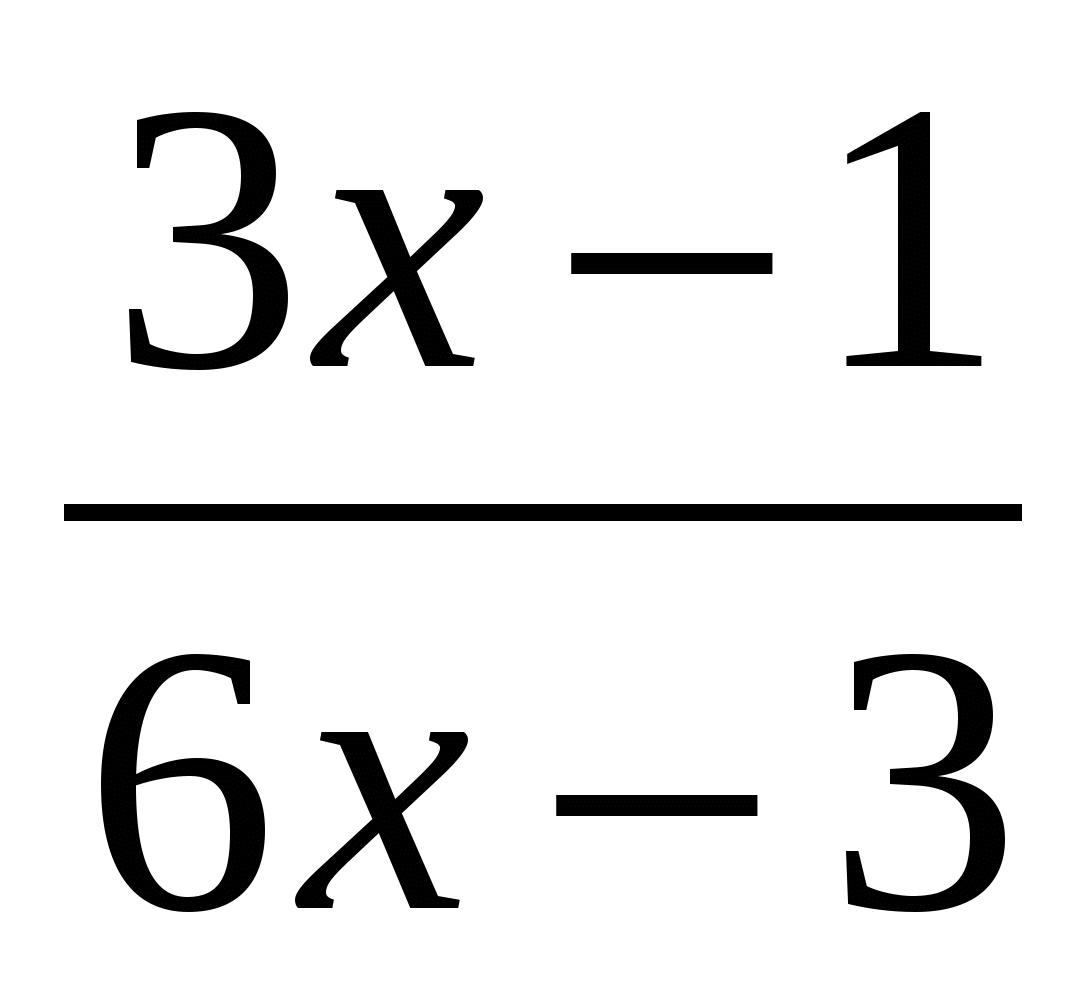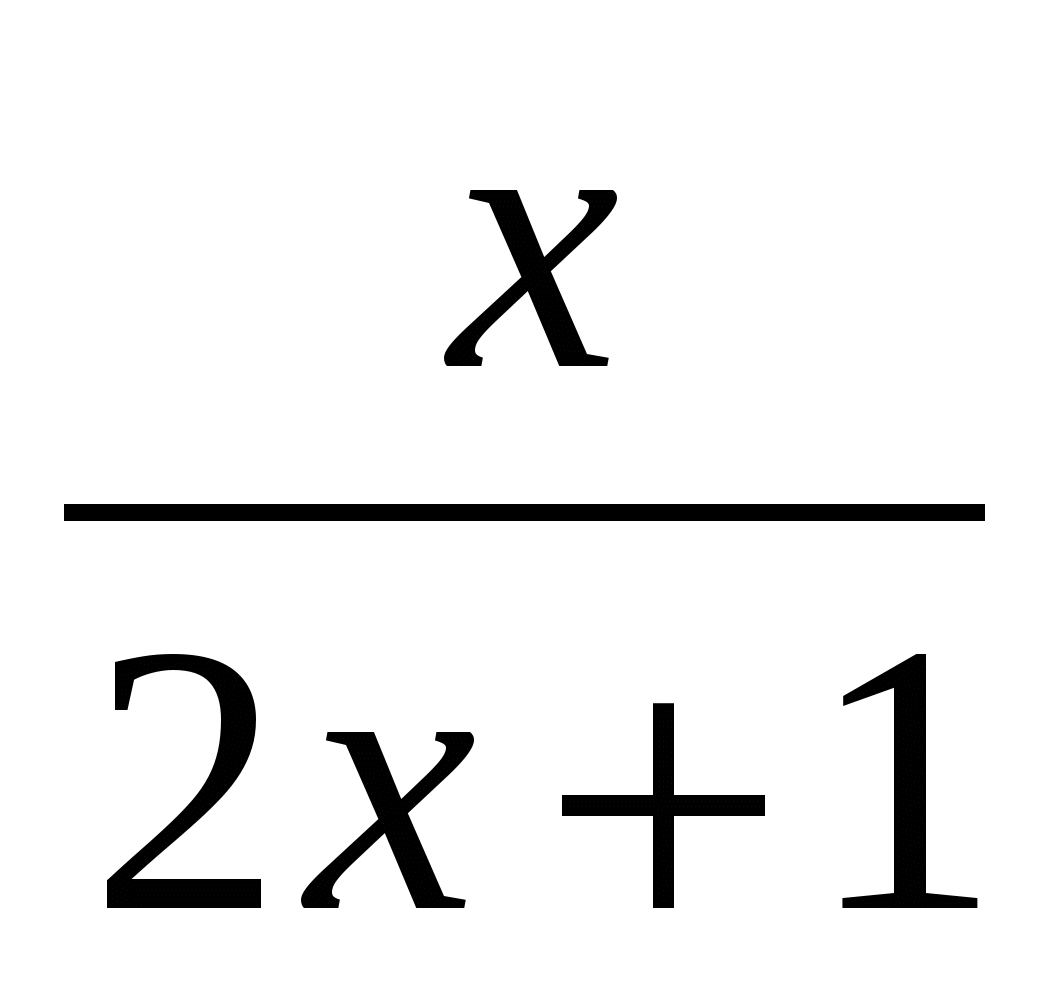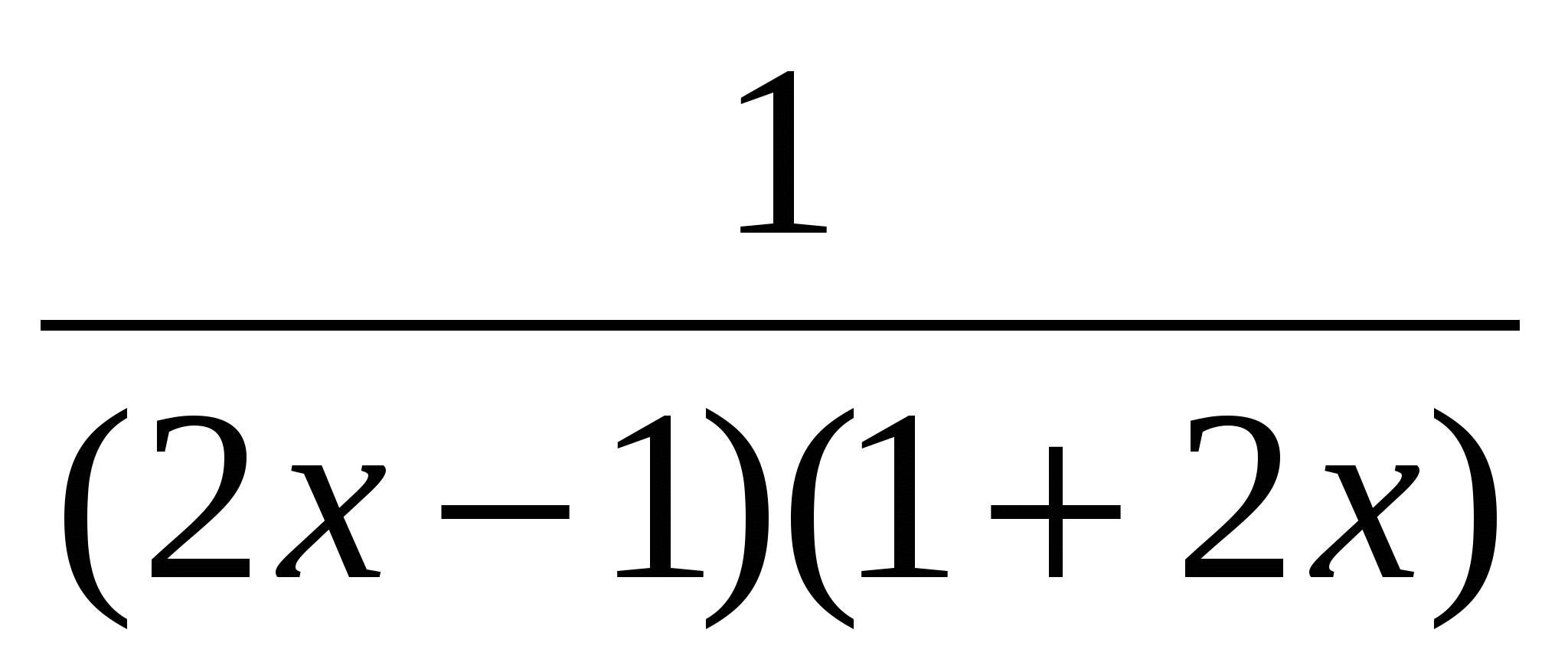=, | ·3(2х-1)(2х+1)

(2х+1)(3х-1)+3=3(2х-1)х,

6х2-2х+3х-1+3=6х2-3х,

5) зразок виконання завдання у парах

№ 250(б)

=
,

О.Д.З.: х≠2,

2- не входить до О.Д.З.

Відповідь. Коренів немає

6) еталон для самоперевірки самостійної роботи

+
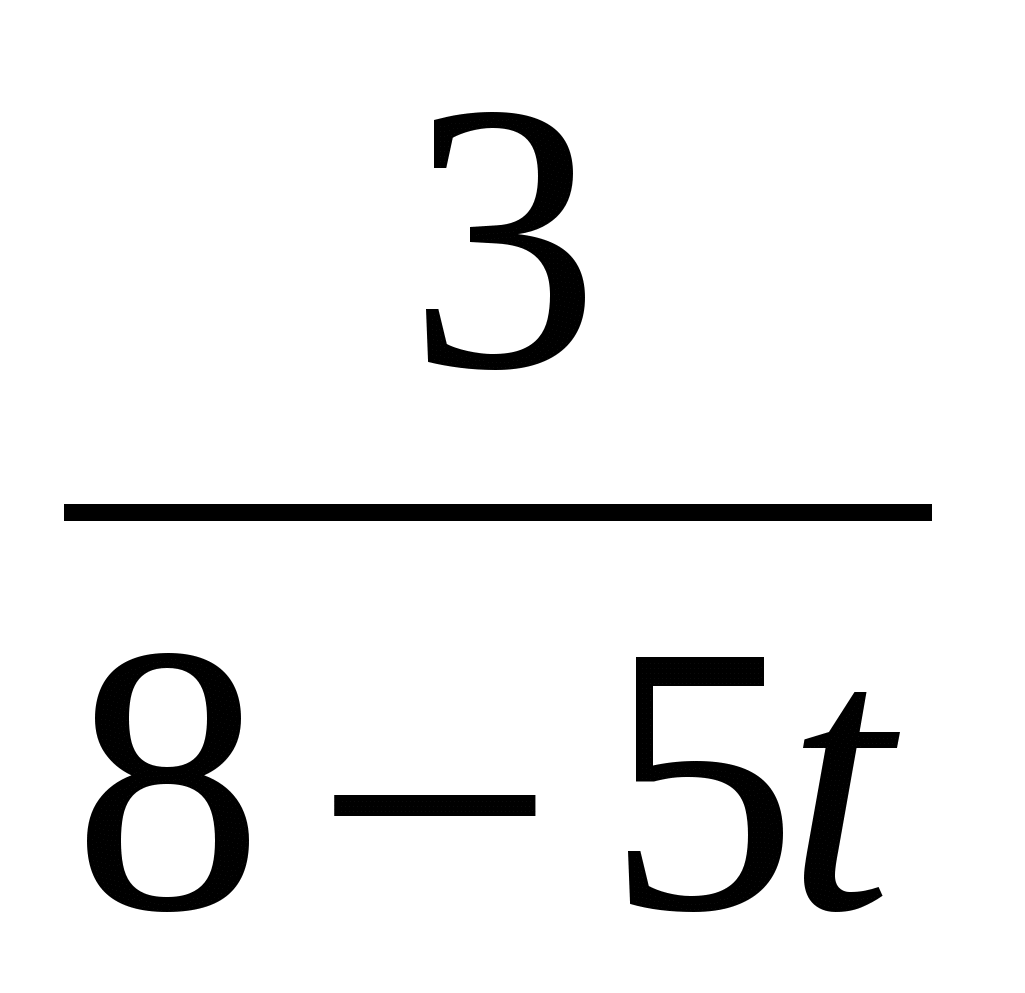=0,

О.Д.З.: t≠1,6; t≠,

=0,

=0,

46t+46=0,

t=1- входить до О.Д.З.

Відповідь. 1.

Хід уроку

1. Самовизначення до навчальної діяльності

- Вітаю! Яку тему ми вивчали під час минулих уроків? (Перетворення раціональних виразів.)

– На минулих уроках ви багато чого навчилися, і ці знання допоможуть сьогодні зробити нове «відкриття».

2. Актуалізація знань та фіксація утруднення в діяльності

Мета етапу:

1) актуалізувати навчальний зміст, необхідний і достатній для сприйняття нового матеріалу: дії з дробами алгебри;

2) актуалізувати розумові операції, необхідні та достатні для сприйняття нового матеріалу: порівняння, аналіз, узагальнення;

3) зафіксувати всі повторювані поняття та алгоритми у вигляді схем та символів;

4) зафіксувати індивідуальне складне становище у діяльності, демонструє на особистісно значимому рівні недостатність наявних знань: вирішити раціональне рівняння.

Організація навчального процесу на етапі 2:

1. На дошці: ··

Від значення яких змінних залежить значення висловлювання? Вкажіть усі допустимі значення змінних.

2. На дошці: +:-

Назвіть порядок дій. Яку формулу скороченого множення застосуйте для розкладання на множники двочлена, що знаходиться у знаменнику 1 дробу? У зошиті виконайте першу дію. (На закритій дошці 1 учень.)

Отже, яка відповідь вийшла? Чи всі отримали таку відповідь? Яку дію потрібно виконати другим? Чи можна виконати одночасно додавання та віднімання алгебраїчних дробів? Чи не вплине це на результат?

Будь ласка, виконайте 2 дію, свою відповідь звірте з відповіддю на дошці. ( Робота в парах).

3. Завдання груп. Розв'яжіть рівняння: -2х=+

Яким алгоритмом користувалися під час вирішення? ( формулюють, вивісити на дошці. Розглянути різні способи вирішення)

4. - Розв'яжіть рівняння: =0. У чому відмінність цього рівняння від попереднього? (У знаменнику змінна). Чи знаєте спосіб його вирішення? (Ні).

3. Виявлення причини утруднення та постановка мети діяльності

Мета етапу:

1) організувати комунікативну взаємодію, під час якої виявляється і фіксується відмінна властивість завдання, що спричинило складне становище у навчальній діяльності;

2) узгодити мету та тему уроку.

Організація навчального процесу на етапі 3:

Що являє собою ліва частина даного рівняння? Що являє собою права частина цього рівняння? Як називаються рівняння такого виду? (Раціональне рівняння)

Тема. Ціль. ( Учні формулюють самі.)

То яке рівняння називають раціональним? ( учні формулюють) Порівняйте з визначенням у підручнику.

4. Побудова проекту виходу із скрути

Мета етапу:

1) організувати комунікативну взаємодію для побудови нового способу дії, що усуває причину виявленої скрути;

2) зафіксувати новий спосіб дії у знаковій, вербальній формі та за допомогою алгоритму.

Організація навчального процесу на етапі 4:

Як ви думаєте, чому виникла скрута при вирішенні заданого рівняння? (Не знаємо способи його вирішення.)

Які пропозиції у Вас виникли? (Скористатися властивістю рівності нулю дробу: (х-9) не може дорівнювати нулю, тому (2х-10) дорівнює 0, звідки знаходимо х=5.)

Завдання груп. Розв'яжіть рівняння : =
-

Яким алгоритмом рішення ви користувалися? (що на початку уроку).

Чи є відмінність при вирішенні цього раціонального рівняння від того, що було вирішено на початку уроку? (Так, необхідно пам'ятати про те, що знаменник дробу не може дорівнювати нулю, тобто знайти область допустимих значень змінної.)

Чи потрібно цю особливість внести до алгоритму розв'язання раціональних рівнянь? (Звичайно.)

-

1) Розкласти знаменник на множники.

2) Знайти область допустимих значень змінної.

3) Привести дроби до спільного знаменника у лівій та правій частинах рівняння.

4) Скористатися правилами:

а) рівності дробу нулю;

б) властивостями пропорції;

в) рівності дробів.

6. Самостійна робота із самоперевіркою за зразком

Мета етапу:

перевірити своє вміння застосовувати новий навчальний зміст у типових умовах на основі зіставлення свого рішення з еталоном для самоперевірки.

Організація навчального процесу на етапі 6:

Роботи перевіряються за зразком. Помилки виправляються, аналізуються, з'ясовується їхня причина.

7. Включення в систему знань та повторення

Мета етапу:

Тренувати навички використання нового змісту спільно з вивченим раніше: розв'язання задач за допомогою системи рівнянь;

Організація навчального процесу на етапі 7:

№241. (Усно.)

8. Рефлексія діяльності на уроці

Мета етапу:

1) зафіксувати новий зміст, вивчений на уроці;

2) оцінити свою діяльність на уроці;

3) подякувати однокласникам, які допомогли отримати результат уроку;

4) зафіксувати невирішені труднощі як напрями майбутньої навчальної діяльності;

5) обговорити та записати домашнє завдання.

Організація навчального процесу на етапі 8:

- Що нового дізналися на уроці?

- Що використовували для "відкриття" нового знання?

– Проаналізуйте свою роботу на уроці.

Домашнє завдання

Рівняння» ми ввели вище в § 7. Спочатку нагадаємо, що таке раціональне вираження. Це - вираз алгебри, складений з чисел і змінної х за допомогою операцій складання, віднімання, множення, поділу і зведення в ступінь з натуральним показником.

Якщо r(х) – раціональний вираз, то рівняння r(х) = 0 називають раціональним рівнянням.

Втім, практично зручніше користуватися дещо ширшим тлумаченням терміну «раціональне рівняння»: це рівняння виду h(x) = q(x), де h(x) і q(x) - раціональні висловлювання.

Досі ми могли вирішити не будь-яке раціональне рівняння, а тільки таке, яке внаслідок різних перетворень та міркувань зводилося до лінійному рівнянню. Тепер наші можливості значно більші: ми зуміємо вирішити раціональне рівняння, яке зводиться не тільки до лінійно-
му, а й до квадратного рівняння.

Нагадаємо, як ми вирішували раціональні рівняння раніше, і спробуємо сформулювати алгоритм розв'язання.

приклад 1.Вирішити рівняння

Рішення. Перепишемо рівняння у вигляді

При цьому, як завжди, ми користуємося тим, що рівності А = В і А - В = 0 виражають ту саму залежність між А і В. Це і дозволило нам перенести член у ліву частину рівняння з протилежним знаком.

Виконаємо перетворення лівої частини рівняння. Маємо

Згадаймо умови рівності дробинулю: тоді, і тільки тоді, коли одночасно виконуються два співвідношення:

1) чисельник дробу дорівнює нулю (а = 0); 2) знаменник дробу відмінний від нуля).
Прирівнявши нулю чисельник дробу в лівій частині рівняння (1), отримаємо

Залишилося перевірити виконання другої зазначеної вище умови. Співвідношення означає рівняння (1), що . Значення х 1 = 2 і х 2 = 0,6 зазначеним співвідношенням задовольняють і тому є корінням рівняння (1), а разом з тим і корінням заданого рівняння.

1) Перетворимо рівняння до виду

2) Виконаємо перетворення лівої частини цього рівняння:

(одночасно змінили знаки в чисельнику та
дроби).
Таким чином, задане рівняння набуває вигляду

3) Розв'яжемо рівняння х 2 - 6x + 8 = 0. Знаходимо

4) Для знайдених значень перевіримо виконання умови . Число 4 цій умові задовольняє, а число 2 - ні. Значить, 4 – корінь заданого рівняння, а 2 – сторонній корінь.
Відповідь: 4.

2. Вирішення раціональних рівнянь методом введення нової змінної

Метод введення нової змінної вам знайомий, ми не раз ним користувалися. Покажемо на прикладах, як він застосовується під час вирішення раціональних рівнянь.

приклад 3.Розв'язати рівняння х 4 + х 2 – 20 = 0.

Рішення. Введемо нову змінну у = х2. Так як х 4 = (х 2) 2 = у 2 то задане рівняння можна переписати у вигляді

у 2 + у – 20 = 0.

Це – квадратне рівняння, коріння якого знайдемо, використовуючи відомі формули; отримаємо у 1 = 4, у 2 = - 5.
Але у = х 2, отже, завдання звелося вирішення двох рівнянь:
x 2 = 4; х 2 =-5.

З першого рівняння знаходимо друге рівняння немає коренів.
Відповідь: .
Рівняння виду ах 4 + bx 2 +c = 0 називають біквадратним рівнянням («бі» - два, тобто як би «двічі квадратне» рівняння). Щойно вирішене рівняння було саме біквадратним. Будь-яке біквадратне рівняння вирішується так само, як рівняння з прикладу 3: вводять нову змінну у = х 2 вирішують отримане квадратне рівняння щодо змінної у, а потім повертаються до змінної х.

приклад 4.Вирішити рівняння

Рішення. Зауважимо, що тут двічі зустрічається те саме вираз х 2 + Зх. Отже, має сенс запровадити нову змінну у = х 2 + Зх. Це дозволить переписати рівняння у більш простому та приємному вигляді (що, власне кажучи, і становить мету введення нової змінної- і запис спрощення
ється, і структура рівняння стає більш ясною):

А тепер скористаємося алгоритмом розв'язання раціонального рівняння.

1) Перенесемо всі члени рівняння в одну частину:

= 0
2) Перетворимо ліву частину рівняння

Отже, ми перетворили задане рівняння на вигляд

3) З рівняння - 7у 2 + 29у -4 = 0 знаходимо (ми з вами вже вирішили досить багато квадратних рівнянь, тому завжди наводити в підручнику докладні викладки, напевно, не варто).

4) Виконаємо перевірку знайденого коріння за допомогою умови 5 (у - 3) (у + 1). Обидва корені цій умові задовольняють.
Отже, квадратне рівняння щодо нової змінної у вирішено:
Оскільки у = х 2 + Зх, а у, як ми встановили, набуває двох значень: 4 і , - нам ще належить вирішити два рівняння: х 2 + Зх = 4; х 2 + Зх =. Корінням першого рівняння є числа 1 і - 4, корінням другого рівняння - числа

У розглянутих прикладах метод запровадження нової змінної був, як люблять висловлюватися математики, адекватний ситуації, т. е. добре їй відповідав. Чому? Та тому, що один і той же вираз явно зустрічався в записі рівняння кілька разів і був сенс позначити цей вираз новою літерою. Але так буває не завжди, іноді нова змінна «виявляється» лише у процесі перетворень. Саме так буде справа в наступному прикладі.

Приклад 5.Вирішити рівняння
х(х-1)(x-2)(x-3) = 24.
Рішення. Маємо
х(х - 3) = х 2 - 3х;
(х - 1) (x - 2) = x 2-Зx +2.

Отже, задане рівняння можна переписати як

(x 2 - 3x) (x 2 + 3x + 2) = 24

Ось тепер нова змінна "проявилася": у = х 2 - Зх.

З її допомогою рівняння можна переписати у вигляді у (у + 2) = 24 і далі у 2 + 2у - 24 = 0. Корінням цього рівняння є числа 4 і -6.

Повертаючись до вихідної змінної х, отримуємо два рівняння х 2 - Зх = 4 та х 2 - Зх = - 6. З першого рівняння знаходимо х 1 = 4, х 2 = - 1; друге рівняння не має коріння.

Відповідь: 4, - 1.

Давайте познайомимося з раціональними та дробовими раціональними рівняннями, дамо їх визначення, наведемо приклади, а також розберемо найпоширеніші типи завдань.

Yandex.RTB R-A-339285-1

Раціональне рівняння: визначення та приклади

Знайомство з раціональними виразами починається у 8 класі школи. У цей час під час уроків алгебри учні дедалі частіше починають зустрічати завдання з рівняннями, які містять раціональні висловлювання у записах. Давайте освіжимо у пам'яті, що це таке.

Визначення 1

Раціональне рівняння- Це таке рівняння, в обох частинах якого містяться раціональні вирази.

У різних посібниках можна зустріти ще одне формулювання.

Визначення 2

Раціональне рівняння- Це таке рівняння, запис лівої частини якого містить раціональний вираз, а права - нуль.

Визначення, які ми привели для раціональних рівнянь, є рівнозначними, оскільки говорять про те саме. Підтверджує правильність наших слів той факт, що для будь-яких раціональних виразів Pі Qрівняння P = Qі P − Q = 0будуть рівносильними виразами.

А тепер звернемося до прикладів.

Приклад 1

Раціональні рівняння:

x = 1 , 2 · x − 12 · x 2 · y · z 3 = 0 , x x 2 + 3 · x - 1 = 2 + 2 7 · x - a · (x + 2) , 1 2 + 3 4 - 12 x - 1 = 3.

Раціональні рівняння так само, як і рівняння інших видів, можуть містити будь-яку кількість змінних від 1 до декількох. Для початку ми розглянемо прості приклади, в яких рівняння будуть містити лише одну змінну. А потім почнемо поступово ускладнювати завдання.

Раціональні рівняння поділяються на дві великі групи: цілі та дробові. Подивимося, які рівняння ставитимуться до кожної групи.

Визначення 3

Раціональне рівняння буде цілим у тому випадку, якщо в записі лівої та правої його частин містяться цілі раціональні вирази.

Визначення 4

Раціональне рівняння буде дробовим у тому випадку, якщо одна або обидві його частини містять дріб.

Дробно раціональні рівняння обов'язково містять поділ на змінну або змінна є в знаменнику. У записі цілих рівнянь такого поділу немає.

Приклад 2

3 · x + 2 = 0і (x + y) · (3 · x 2 − 1) + x = − y + 0 , 5- Цілі раціональні рівняння. Тут обидві частини рівняння представлені цілими виразами.

1 x - 1 = x 3 та x: (5 · x 3 + y 2) = 3: (x − 1) : 5– це дрібно раціональні рівняння.

До цілих раціональних рівнянь можна віднести лінійні та квадратні рівняння.

Вирішення цілих рівнянь

Розв'язання таких рівнянь зазвичай зводиться до перетворення їх на рівносильні рівняння алгебри. Досягти цього можна шляхом проведення рівносильних перетворень рівнянь відповідно до наступного алгоритму:

• спочатку отримаємо нуль у правій частині рівняння, при цьому необхідно перенести вираз, що у правої частини рівняння, у його ліву частину і поміняти знак;
• потім перетворимо вираз у лівій частині рівняння в багаточлен стандартного вигляду.

Ми повинні отримати рівняння алгебри. Це рівняння буде рівносильним по відношенню до вихідного рівняння. Легкі випадки дозволяють нам вирішити завдання звести ціле рівняння з лінійному чи квадратному. У випадку ми вирішуємо алгебраїчне рівняння ступеня n.

Приклад 3

Необхідно знайти коріння цілого рівняння 3 · (x + 1) · (x - 3) = x · (2 ​​· x - 1) - 3.

Рішення

Проведемо перетворення вихідного виразу з метою отримати рівносильне йому рівняння алгебри. Для цього зробимо перенесення виразу, що міститься у правій частині рівняння, в ліву частину та замінимо знак на протилежний. У результаті отримаємо: 3 · (x + 1) · (x - 3) - x · (2 ​​· x - 1) + 3 = 0.

Тепер проведемо перетворення виразу, яке знаходиться в лівій частині в багаточлен стандартного виду і зробимо необхідні дії з цим багаточленом:

3 · (x + 1) · (x - 3) - x · (2 ​​· x - 1) + 3 = (3 · x + 3) · (x - 3) - 2 · x 2 + x + 3 = = 3 · x 2 − 9 · x + 3 · x − 9 − 2 · x 2 + x + 3 = x 2 − 5 · x − 6

У нас вдалося звести рішення вихідного рівняння до розв'язання квадратного рівняння виду x 2 − 5 · x − 6 = 0. Дискримінант цього рівняння позитивний: D = (−5) 2 − 4 · 1 · (− 6) = 25 + 24 = 49 .Це означає, дійсних коренів буде два. Знайдемо їх, скориставшись формулою коренів квадратного рівняння:

x = - - 5 ± 49 2 · 1

x 1 = 5 + 7 2 або x 2 = 5 - 7 2

x 1 = 6 або x 2 = - 1

Перевіримо вірність коренів рівняння, що ми знайшли у ході рішення. Для цього числа, які ми отримали, підставимо у вихідне рівняння: 3 · (6 + 1) · (6 - 3) = 6 · (2 ​​· 6 - 1) - 3і 3 · (− 1 + 1) · (− 1 − 3) = (− 1) · (2 ​​· (− 1) − 1) − 3. В першому випадку 63 = 63 , у другому 0 = 0 . Коріння x = 6і x = − 1справді є корінням рівняння, даного за умови прикладу.

Відповідь: 6 , − 1 .

Давайте розберемо, що означає «ступінь цілого рівняння». З цим терміном ми часто зустрічатимемося у тих випадках, коли нам треба буде уявити ціле рівняння у вигляді алгебраїчного. Дамо визначення поняття.

Визначення 5

Ступінь цілого рівняння- Це ступінь рівняння алгебри, рівносильного вихідного цілого рівняння.

Якщо подивитися на рівняння прикладу, наведеного вище, можна встановити: ступінь даного цілого рівняння другий.

Якби наш курс обмежувався рішенням рівнянь другого ступеня, то розгляд теми можна було б закінчити. Але все не так просто. Вирішення рівнянь третього ступеня пов'язане з труднощами. А для рівнянь вище четвертого ступеня і не існує загальних формул коренів. У зв'язку з цим рішення цілих рівнянь третього, четвертого та інших ступенів вимагає від нас застосування цілого ряду інших прийомів та методів.

Найчастіше використовується підхід до вирішення цілих раціональних рівнянь, який ґрунтується на методі розкладання на множники. Алгоритм дій у разі наступний:

• переносимо вираз із правої частини в ліву для того, щоб у правій частині запису залишився нуль;
• представляємо вираз у лівій частині як добуток множників, а потім переходимо до сукупності кількох більш простих рівнянь.

Знайдіть розв'язок рівняння (x 2 − 1) · (x 2 − 10 · x + 13) = 2 · x · (x 2 − 10 · x + 13) .

Рішення

Переносимо вираз із правої частини запису до лівої з протилежним знаком: (x 2 − 1) · (x 2 − 10 · x + 13) − 2 · x · (x 2 − 10 · x + 13) = 0. Перетворення лівої частини на багаточлен стандартного виду недоцільно у зв'язку з тим, що це дасть нам рівняння алгебри четвертого ступеня: x 4 − 12 · x 3 + 32 · x 2 − 16 · x − 13 = 0. Легкість перетворення не виправдовує всіх труднощів із рішенням такого рівняння.

Набагато простіше піти іншим шляхом: винесемо за дужки спільний множник x 2 − 10 · x + 13 .Так ми прийдемо до рівняння виду (x 2 − 10 · x + 13) · (x 2 − 2 · x − 1) = 0. Тепер замінимо отримане рівняння сукупністю двох квадратних рівнянь x 2 − 10 · x + 13 = 0і x 2 − 2 · x − 1 = 0і знайдемо їх коріння через дискримінант: 5 + 2 · 3, 5 - 2 · 3, 1 + 2, 1 - 2.

Відповідь: 5 + 2 · 3, 5-2 · 3, 1 + 2, 1-2.

Так само ми можемо використовувати метод введення нової змінної. Цей метод дозволяє нам переходити до рівносильних рівнянь зі ступенями нижчими, ніж були ступеня у вихідному цілому рівнянні.

Приклад 5

Чи є коріння у рівняння (x 2 + 3 · x + 1) 2 + 10 = − 2 · (x 2 + 3 · x − 4)?

Рішення

Якщо ми зараз спробуємо звести ціле раціональне рівняння до алгебраїчного, то отримаємо рівняння 4 ступеня, яке не має раціонального коріння. Тому нам буде простіше піти іншим шляхом: ввести нову змінну у, яка замінить у рівнянні вираз x 2 + 3 · x.

Тепер ми працюватимемо з цілим рівнянням (y + 1) 2 + 10 = − 2 · (y − 4). Перенесемо праву частину рівняння до лівої з протилежним знаком і проведемо необхідні перетворення. Отримаємо: y 2 + 4 · y + 3 = 0. Знайдемо коріння квадратного рівняння: y = − 1і y = − 3.

Тепер проведемо зворотну заміну. Отримаємо два рівняння x 2 + 3 · x = − 1і x 2 + 3 · x = − 3 .Перепишемо їх як x 2 + 3 · x + 1 = 0 x 2 + 3 · x + 3 = 0. Використовуємо формулу коренів квадратного рівняння для того, щоб знайти коріння першого рівняння з одержаних: - 3 ± 5 2 . Дискримінант другого рівняння негативний. Це означає, що справжнього коріння другого рівняння немає.

Відповідь:- 3 ± 5 2

Цілі рівняння високих ступенів трапляються у завданнях досить часто. Лякатися їх не потрібно. Потрібно бути готовим застосувати нестандартний метод їх вирішення, у тому числі ряд штучних перетворень.

Розв'язання дробово раціональних рівнянь

Почнемо розгляд цієї підтеми з алгоритму розв'язання дробово раціональних рівнянь виду p (x) q (x) = 0 , де p(x)і q (x)- Цілі раціональні вирази. Вирішення інших дробово раціональних рівнянь завжди можна звести до розв'язання рівнянь зазначеного виду.

В основу найбільш уживаного методу розв'язання рівнянь p(x) q(x) = 0 покладено таке твердження: числовий дріб u v, де v- Це число, яке відмінно від нуля, дорівнює нулю тільки в тих випадках, коли чисельник дробу дорівнює нулю. Дотримуючись логіки наведеного твердження, ми можемо стверджувати, що рішення рівняння p(x) q(x) = 0 може бути зведене у виконанні двох умов: p(x) = 0і q (x) ≠ 0. На цьому побудовано алгоритм розв'язання дробових раціональних рівнянь виду p(x) q(x) = 0:

• знаходимо рішення цілого раціонального рівняння p(x) = 0;
• перевіряємо, чи виконується для коренів, знайдених у ході рішення, умова q (x) ≠ 0.

Якщо ця умова виконується, то знайдений корінь. Якщо ні, то корінь не є рішенням задачі.

Приклад 6

Знайдемо коріння рівняння 3 · x - 2 5 · x 2 - 2 = 0.

Рішення

Ми маємо справу з дробовим раціональним рівнянням виду p (x) q (x) = 0, в якому p (x) = 3 · x − 2, q (x) = 5 · x 2 − 2 = 0 . Приступимо до вирішення лінійного рівняння 3 · x − 2 = 0. Коренем цього рівняння буде x = 2 3.

Проведемо перевірку знайденого кореня, чи він задовольняє умові 5 · x 2 − 2 ≠ 0. Для цього підставимо числове значення у вираз. Отримаємо: 5 · 2 3 2 - 2 = 5 · 4 9 - 2 = 20 9 - 2 = 2 9 ≠ 0 .

Умова виконується. Це означає що x = 2 3є коренем вихідного рівняння.

Відповідь: 2 3 .

Є ще один варіант розв'язання дробових раціональних рівнянь p(x)q(x)=0. Згадаймо, що це рівняння рівносильне цілому рівнянню p(x) = 0на ділянці допустимих значень змінної x вихідного рівняння. Це дозволяє нам використовувати наступний алгоритм у розв'язанні рівнянь p(x) q(x) = 0:

• вирішуємо рівняння p(x) = 0;
• знаходимо область допустимих значень змінної x;
• беремо коріння, яке лежить в області допустимих значень змінної x , як шукане коріння вихідного дробового раціонального рівняння.

Розв'яжіть рівняння x 2 - 2 · x - 11 x 2 + 3 · x = 0 .

Рішення

Для початку вирішимо квадратне рівняння x 2 − 2 · x − 11 = 0. Для обчислення його коріння ми використовуємо формулу коренів для парного другого коефіцієнта. Отримуємо D 1 = (−1) 2 − 1 · (− 11) = 12і x = 1 ± 2 3 .

Тепер ми можемо знайти ОДЗ змінної x для вихідного рівняння. Це все числа, для яких x 2 + 3 · x ≠ 0. Це те саме, що x · (x + 3) ≠ 0, звідки x ≠ 0 , x ≠ − 3 .

Тепер перевіримо, чи входять отримані першому етапі рішення коріння x = 1 ± 2 3 в область допустимих значень змінної x . Ми бачимо, що входять. Це означає, що вихідне раціональне дробове рівняння має два корені x = 1 ± 2 3 .

Відповідь: x = 1 ± 2 3

Другий описаний метод рішення простіше першого у випадках, коли легко знаходиться область допустимих значень змінної x , а корені рівняння p(x) = 0ірраціональні. Наприклад, 7 ± 4 · 26 9 . Коріння може бути і раціональним, але з великим чисельником або знаменником. Наприклад, 127 1101 і − 31 59 . Це дозволяє заощадити час на проведенні перевірки умови q (x) ≠ 0: набагато простіше виключити коріння, яке не підходить, по ОДЗ

У тих випадках, коли коріння рівняння p(x) = 0цілі, доцільніше використовувати перший із описаних алгоритмів розв'язання рівнянь виду p(x) q(x) = 0 . Швидше одразу знаходити коріння цілого рівняння p(x) = 0, після чого перевіряти, чи виконується для них умова q (x) ≠ 0, а не знаходити ОДЗ, після чого вирішувати рівняння p(x) = 0на цій ОДЗ. Це з тим, що у разі зробити перевірку зазвичай простіше, ніж знайти ОДЗ.

Приклад 8

Знайдіть корені рівняння (2 · x - 1) · (x - 6) · (x 2 - 5 · x + 14) · (x + 1) x 5 - 15 · x 4 + 57 · x 3 - 13 · x 2 + 26 · x + 112 = 0.

Рішення

Почнемо з розгляду цілого рівняння (2 · x - 1) · (x - 6) · (x 2 - 5 · x + 14) · (x + 1) = 0та знаходження його коріння. Для цього застосуємо метод розв'язання рівнянь через розкладання на множники. Виходить, що вихідне рівняння рівносильне сукупності чотирьох рівнянь 2 · x - 1 = 0, x - 6 = 0, x 2 - 5 · x + 14 = 0, x + 1 = 0, з яких три лінійних і одне квадратне. Знаходимо коріння: з першого рівняння x = 1 2, з другого – x = 6з третього – x = 7 , x = − 2 , з четвертого – x = − 1.

Проведемо перевірку отриманого коріння. Визначити ОДЗ у разі нам складно, оскільки цього доведеться провести рішення алгебраїчного рівняння п'ятого ступеня. Простіше буде перевірити умову, за якою знаменник дробу, що знаходиться в лівій частині рівняння, не повинен звертатися в нуль.

По черзі підставимо коріння на місце змінної х у вираз x 5 − 15 · x 4 + 57 · x 3 − 13 · x 2 + 26 · x + 112і обчислимо його значення:

1 2 5 − 15 · 1 2 4 + 57 · 1 2 3 − 13 · 1 2 2 + 26 · 1 2 + 112 = = 1 32 − 15 16 + 57 8 − 13 4 + 13 + 112 = 12 + ≠ 0;

6 5 − 15 · 6 4 + 57 · 6 3 − 13 · 6 2 + 26 · 6 + 112 = 448 ≠ 0;

7 5 − 15 · 7 4 + 57 · 7 3 − 13 · 7 2 + 26 · 7 + 112 = 0;

(−2) 5−15 · (−2) 4 + 57 · (−2) 3 − 13 · (−2) 2 + 26 · (−2) + 112 = − 720 ≠ 0 ;

(−1) 5−15 · (−1) 4 + 57 · (−1) 3−13 · (−1) 2 + 26 · (−1) + 112 = 0 .

Проведена перевірка дозволяє нам встановити, що корінням вихідного дробового рацинального рівняння є 1 2 , 6 − 2 .

Відповідь: 1 2 , 6 , - 2

Приклад 9

Знайдіть коріння дробового раціонального рівняння 5 · x 2 - 7 · x - 1 · x - 2 x 2 + 5 · x - 14 = 0.

Рішення

Почнемо роботу з рівнянням (5 · x 2 − 7 · x − 1) · (x − 2) = 0. Знайдемо його коріння. Нам простіше уявити це рівняння як сукупність квадратного та лінійного рівнянь 5 · x 2 − 7 · x − 1 = 0і x − 2 = 0.

Використовуємо формулу коренів квадратного рівняння для пошуку коренів. Отримуємо з першого рівняння два корені x = 7 ± 69 10 , а з другого x = 2.

Підставляти значення коріння у вихідне рівняння для перевірки умов нам буде досить складно. Простіше буде визначити ОДЗ змінної x. В даному випадку ОДЗ змінної x - це все числа, крім тих, для яких виконується умова x 2 + 5 · x − 14 = 0. Отримуємо: x ∈ - ∞ , - 7 ∪ - 7 , 2 ∪ 2 , + ∞ .

Тепер перевіримо, чи належать знайдене нами коріння до області допустимих значень змінної x .

Коріння x = 7 ± 69 10 - належать, тому вони є корінням вихідного рівняння, а x = 2– не належить, тому це сторонній корінь.

Відповідь: x = 7 ± 69 10 .

Розберемо окремо випадки, коли у чисельнику дробового раціонального рівняння виду p(x)q(x) = 0 знаходиться число. У таких випадках, якщо в чисельнику знаходиться число, відмінне від нуля, то рівняння не матиме коріння. Якщо це число дорівнюватиме нулю, то коренем рівняння буде будь-яке число з ОДЗ.

Приклад 10

Розв'яжіть дробове раціональне рівняння - 3, 2 x 3 + 27 = 0.

Рішення

Дане рівняння не матиме коренів, тому що в чисельнику дробу з лівої частини рівняння знаходиться відмінне від нуля число. Це означає, що при жодних значеннях x значення наведеного в умові завдання дробу не дорівнюватиме нулю.

Відповідь:немає коріння.

Приклад 11

Розв'яжіть рівняння 0 x 4 + 5 · x 3 = 0 .

Рішення

Так як в чисельнику дробу знаходиться нуль, розв'язуванням рівняння буде будь-яке значення x з ОДЗ змінної x .

Тепер визначимо ОДЗ. Воно буде включати всі значення x , за яких x 4 + 5 · x 3 ≠ 0. Рішеннями рівняння x 4 + 5 · x 3 = 0є 0 і − 5 , так як це рівняння рівносильне рівнянню x 3 · (x + 5) = 0, а воно у свою чергу рівносильне сукупності двох рівнянь x 3 = 0 x + 5 = 0, звідки і видно це коріння. Ми приходимо до того, що областю допустимих значень є будь-які x , крім x = 0і x = − 5.

Виходить, що дробове раціональне рівняння 0 x 4 + 5 · x 3 = 0 має безліч рішень, якими є будь-які числа крім нуля і - 5 .

Відповідь: - ∞ , - 5 ∪ (- 5 , 0 ∪ 0 , + ∞

Тепер поговоримо про дробові раціональні рівняння довільного виду та методи їх вирішення. Їх можна записати як r(x) = s(x), де r(x)і s(x)– раціональні висловлювання, причому хоча б один із них дробовий. Розв'язання таких рівнянь зводиться до розв'язання рівнянь виду p(x) q(x) = 0 .

Ми вже знаємо, що ми можемо отримати рівносильне рівняння при перенесенні виразу з правої частини рівняння до лівого з протилежним знаком. Це означає, що рівняння r(x) = s(x)рівносильне рівняння r(x) − s(x) = 0. Також ми вже розібрали способи перетворення раціонального вираження на раціональний дріб. Завдяки цьому ми легко можемо перетворити рівняння r(x) − s(x) = 0в тотожний йому раціональний дріб виду p (x) q (x) .

Так ми переходимо від вихідного дробового раціонального рівняння r(x) = s(x)до рівняння виду p (x) q (x) = 0, вирішувати які ми вже навчилися.

Слід враховувати, що під час проведення переходів від r(x) − s(x) = 0 p (x) q (x) = 0 , а потім до p(x) = 0ми можемо не враховувати розширення області допустимих значень змінної x.

Цілком реальна ситуація, коли вихідне рівняння r(x) = s(x)та рівняння p(x) = 0внаслідок перетворень перестануть бути рівносильними. Тоді рішення рівняння p(x) = 0може дати нам коріння, яке буде стороннім для r(x) = s(x). У зв'язку з цим у кожному випадку необхідно проводити перевірку будь-яким із описаних вище способів.

Щоб полегшити роботу з вивчення теми, ми узагальнили всю інформацію в алгрітм рішення дробового раціонального рівняння виду r(x) = s(x):

• переносимо вираз із правої частини з протилежним знаком і отримуємо праворуч нуль;
• перетворимо вихідний вираз у раціональний дріб p (x) q (x) , послідовно виконуючи дії з дробами та багаточленами;
• вирішуємо рівняння p(x) = 0;
• виявляємо стороннє коріння шляхом перевірки їх належності ОДЗ або методом підстановки у вихідне рівняння.

Візуально ланцюжок дій виглядатиме так:

r (x) = s (x) → r (x) - s (x) = 0 → p (x) q (x) = 0 → p (x) = 0 → відс і в а н і е п о с т о р о н і х к о р н й

Приклад 12

Розв'яжіть дробове раціональне рівняння x x + 1 = 1 x + 1 .

Рішення

Перейдемо до рівняння x x + 1 – 1 x + 1 = 0 . Перетворимо дробовий раціональний вираз у лівій частині рівняння до виду p(x)q(x).

Для цього нам доведеться привести раціональні дроби до спільного знаменника та спростити вираз:

x x + 1 - 1 x - 1 = x · x - 1 · (x + 1) - 1 · x · (x + 1) x · (x + 1) = = x 2 - x - 1 - x 2 - x x · (x + 1) = - 2 · x - 1 x · (x + 1)

Для того, щоб знайти коріння рівняння - 2 · x - 1 x · (x + 1) = 0 нам необхідно вирішити рівняння − 2 · x − 1 = 0. Отримуємо один корінь x = - 1 2.

Нам залишилося виконати перевірку будь-яким із методів. Розглянемо їх обоє.

Підставимо отримане значення у вихідне рівняння. Отримаємо - 1 2 - 1 2 + 1 = 1 - 1 2 + 1 . Ми прийшли до вірної числової рівності − 1 = − 1 . Це означає що x = − 1 2є коренем вихідного рівняння.

Тепер проведемо перевірку через ОДЗ. Визначимо область допустимих значень змінної x. Це буде безліч чисел, за винятком − 1 і 0 (при x = − 1 і x = 0 перетворюються на нуль знаменники дробів). Отриманий нами корінь x = − 1 2належить ОДЗ. Це означає, що він є коренем вихідного рівняння.

Відповідь: − 1 2 .

Приклад 13

Знайдіть корені рівняння x 1 x + 3 - 1 x = - 2 3 · x.

Рішення

Ми маємо справу з дрібним раціональним рівнянням. Отже, діятимемо за алгоритмом.

Перенесемо вираз із правої частини до лівої з протилежним знаком: x 1 x + 3 - 1 x + 2 3 · x = 0

Проведемо необхідні перетворення: x 1 x + 3 - 1 x + 2 3 · x = x 3 + 2 · x 3 = 3 · x 3 = x.

Приходимо до рівняння x = 0. Корінь цього рівняння – нуль.

Перевіримо, чи це корінь стороннім для вихідного рівняння. Підставимо значення вихідне рівняння: 0 1 0 + 3 - 1 0 = - 2 3 · 0 . Як бачите, отримане рівняння не має сенсу. Це означає, що 0 – це сторонній корінь, а вихідне дробове раціональне рівняння коренів немає.

Відповідь:немає коріння.

Якщо ми не включили в алгоритм інші рівносильні перетворення, це зовсім не означає, що ними не можна користуватися. Алгоритм універсальний, але він створений для того, щоб допомагати, а не обмежувати.

Приклад 14

Розв'яжіть рівняння 7 + 1 3 + 1 2 + 1 5 - x 2 = 7 7 24

Рішення

Найпростіше буде вирішити наведене дробове раціональне рівняння згідно з алгоритмом. Але є й інший шлях. Розглянемо його.

Віднімемо від правої та лівої частин 7, отримуємо: 1 3 + 1 2 + 1 5 - x 2 = 7 24 .

Звідси можна зробити висновок, що вираз у знаменнику лівої частини має дорівнювати числу, зворотному числу з правої частини, тобто, 3 + 1 2 + 1 5 - x 2 = 24 7 .

Віднімемо з обох частин 3: 1 2 + 1 5 - x 2 = 3 7 . За аналогією 2 + 1 5 - x 2 = 7 3 , звідки 1 5 - x 2 = 1 3 і далі 5 - x 2 = 3 , x 2 = 2 , x = ± 2

Проведемо перевірку для того, щоб встановити, чи є знайдене коріння корінням вихідного рівняння.

Відповідь: x = ±2

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Презентація та урок на тему: "Раціональні рівняння. Алгоритм та приклади вирішення раціональних рівнянь"

Додаткові матеріали
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання! Усі матеріали перевірені антивірусною програмою.

Навчальні посібники та тренажери в інтернет-магазині "Інтеграл" для 8 класу
Посібник до підручника Макарічева Ю.М. Посібник до підручника Мордковича О.Г.

Знайомство з ірраціональними рівняннями

Нехай $r(x)$ – це раціональний вираз. Такий вираз може являти собою простий багаточлен від змінної $х$ або відношення багаточленів (вводиться операція поділу, як для раціональних чисел).
Рівняння $ r (x) = 0 $ називається раціональним рівнянням.
Будь-яке рівняння виду $p(x)=q(x)$, де $p(x)$ і $q(x)$ – раціональні вирази, також буде раціональним рівнянням.

Розглянемо приклади розв'язання раціональних рівнянь.

Рішення.
Перенесемо всі вирази в ліву частину: $ frac (5x-3) (x-3) - frac (2x-3) (x) = 0 $.
Якби в лівій частині рівняння були представлені звичайні числа, ми привели б два дроби до спільного знаменника.
Давайте так і зробимо: $\frac((5x-3)*x)((x-3)*x)-\frac((2x-3)*(x-3))((x-3)*x )=\frac(5x^2-3x-(2x^2-6x-3x+9))((x-3)*x)=\frac(3x^2+6x-9)((x-3) *x)=\frac(3(x^2+2x-3))((x-3)*x)$.
Отримали рівняння: $\frac(3(x^2+2x-3))((x-3)*x)=0$.

Дроб дорівнює нулю, тоді і тільки тоді, коли чисельник дробу дорівнює нулю, а знаменник відмінний від нуля. Тоді окремо прирівняємо чисельник до нуля і знайдемо коріння чисельника.
$3(x^2+2x-3)=0$ або $x^2+2x-3=0$.
$x_(1,2)=frac(-2±sqrt(4-4*(-3)))(2)=frac(-2±4)(2)=1;-3$.
Тепер перевіримо знаменник дробу: $(x-3)*x≠0$.
Добуток двох чисел дорівнює нулю, коли хоча б одне з цих чисел дорівнює нулю. Тоді: $x≠0$ або $x-3≠0$.
$x≠0$ або $x≠3$.
Коріння, отримані в чисельнику та знаменнику, не збігаються. Значить у відповідь записуємо обидва корені чисельника.
Відповідь: $ х = 1 $ або $ х = -3 $.

Якщо раптом, один з коренів чисельника збігся з коренем знаменника, його слід виключити. Таке коріння називається стороннім!

Алгоритм розв'язання раціональних рівнянь:

приклад 2.
Розв'яжіть рівняння: $frac(3x)(x-1)+frac(4)(x+1)=frac(6)(x^2-1)$.

Рішення.
Вирішимо згідно з пунктами алгоритму.
1. $\frac(3x)(x-1)+\frac(4)(x+1)-\frac(6)(x^2-1)=0$.
2. $\frac(3x)(x-1)+\frac(4)(x+1)-\frac(6)(x^2-1)=\frac(3x)(x-1)+\ frac(4)(x+1)-\frac(6)((x-1)(x+1))= \frac(3x(x+1)+4(x-1)-6)((x -1)(x+1))=$ $=\frac(3x^2+3x+4x-4-6)((x-1)(x+1))=\frac(3x^2+7x- 10)((x-1)(x+1))$.
$\frac(3x^2+7x-10)((x-1)(x+1))=0$.
3. Прирівняємо чисельник до нуля: $3x^2+7x-10=0$.
$x_(1,2)=\frac(-7±\sqrt(49-4*3*(-10)))(6)=\frac(-7±13)(6)=-3\frac( 1) (3); 1 $.
4. Прирівняємо знаменник до нуля:
$(x-1)(x+1)=0$.
$x=1$ і $x=-1$.
Один із коренів $х=1$ збігся з коренем із чисельника, тоді ми його у відповідь не записуємо.
Відповідь: $ х = -1 $.

Вирішувати раціональні рівняння зручно за допомогою методу заміни змінних. Давайте продемонструємо це.

приклад 3.
Розв'язати рівняння: $x^4+12x^2-64=0$.

Рішення.
Введемо заміну: $ t = x ^ 2 $.
Тоді наше рівняння набуде вигляду:
$t^2+12t-64=0$ - звичайне квадратне рівняння.
$t_(1,2)=\frac(-12±\sqrt(12^2-4*(-64)))(2)=\frac(-12±20)(2)=-16; 4 $.
Введемо зворотну заміну: $ x ^ 2 = 4 $ або $ x ^ 2 = -16 $.
Корінням першого рівняння є пара чисел $х=±2$. Друге – не має коріння.
Відповідь: $ х = ± 2 $.

приклад 4.
Розв'язати рівняння: $x^2+x+1=\frac(15)(x^2+x+3)$.
Рішення.
Введемо нову змінну: $ t = x ^ 2 + x + 1 $.
Тоді рівняння набуде вигляду: $t=\frac(15)(t+2)$.
Далі діятимемо за алгоритмом.
1. $t-\frac(15)(t+2)=0$.
2. $\frac(t^2+2t-15)(t+2)=0$.
3. $ t 2 +2 t-15 = 0 $.
$t_(1,2)=\frac(-2±\sqrt(4-4*(-15)))(2)=\frac(-2±\sqrt(64))(2)=\frac( -2±8)(2)=-5; 3 $.
4. $t≠-2$ - коріння не співпадає.
Введемо зворотну заміну.
$x^2+x+1=-5$.
$x^2+x+1=3$.
Розв'яжемо кожне рівняння окремо:
$x^2+x+6=0$.
$x_(1,2)=\frac(-1±\sqrt(1-4*(-6)))(2)=\frac(-1±\sqrt(-23))(2)$ - ні коріння.
І друге рівняння: $ x ^ 2 + x-2 = 0 $.
Корінням цього рівняння будуть числа $х=-2$ і $х=1$.
Відповідь: $ х = -2 $ і $ х = 1 $.

Приклад 5.
Розв'язати рівняння: $x^2+\frac(1)(x^2) +x+\frac(1)(x)=4$.

Рішення.
Введемо заміну: $ t = x + \ frac (1) (x) $.
Тоді:
$t^2=x^2+2+\frac(1)(x^2)$ або $x^2+\frac(1)(x^2)=t^2-2$.
Здобули рівняння: $t^2-2+t=4$.
$ t 2 + t-6 = 0 $.
Корінням даного рівняння є пара:
$ t = -3 $ і $ t = 2 $.
Введемо зворотну заміну:
$x+\frac(1)(x)=-3$.
$ x + \ frac (1) (x) = 2 $.
Вирішимо окремо.
$x+\frac(1)(x)+3=0$.
$\frac(x^2+3x+1)(x)=0$.
$x_(1,2)=frac(-3±sqrt(9-4))(2)=frac(-3±sqrt(5))(2)$.
Розв'яжемо друге рівняння:
$ x + \ frac (1) (x) -2 = 0 $.
$\frac(x^2-2x+1)(x)=0$.
$\frac((x-1)^2)(x)=0$.
Коренем цього рівняння є число $х = 1 $.
Відповідь: $x=\frac(-3±\sqrt(5))(2)$, $x=1$.

Завдання для самостійного вирішення

1. $\frac(3x+2)(x)=\frac(2x+3)(x+2)$.

2. $\frac(5x)(x+2)-\frac(20)(x^2+2x)=\frac(4)(x)$.
3. $x^4-7x^2-18=0$.
4. $2x^2+x+2=\frac(8)(2x^2+x+4)$.
5. $(x+2)(x+3)(x+4)(x+5)=3$.

Ми вже навчилися розв'язувати квадратні рівняння. Тепер поширимо вивчені методи на раціональні рівняння.

Що таке раціональний вираз? Ми вже стикалися з цим поняттям. Раціональними виразаминазиваються вирази, складені з чисел, змінних, їх ступенів та знаків математичних дій.

Відповідно, раціональними рівняннями називаються рівняння виду: , де - Раціональні висловлювання.

Раніше ми розглядали лише ті раціональні рівняння, що зводяться до лінійних. Тепер розглянемо і ті раціональні рівняння, які зводяться до квадратних.

Приклад 1

Вирішити рівняння: .

Рішення:

Дроб дорівнює 0 тоді і лише тоді, коли її чисельник дорівнює 0, а знаменник не дорівнює 0.

Отримуємо таку систему:

Перше рівняння системи – це квадратне рівняння. Перш ніж його вирішувати, поділимо всі його коефіцієнти на 3. Отримаємо:

Отримуємо два корені: ; .

Оскільки 2 ніколи не дорівнює 0, необхідно, щоб виконувались дві умови: . Оскільки жоден із отриманих вище коренів рівняння не збігається з неприпустимими значеннями змінної, які вийшли при вирішенні другої нерівності, вони обидва є рішеннями цього рівняння.

Відповідь:.

Отже, давайте сформулюємо алгоритм розв'язання раціональних рівнянь:

1. Перенести всі складові до лівої частини, щоб у правій частині вийшов 0.

2. Перетворити та спростити ліву частину, привести всі дроби до спільного знаменника.

3. Отриманий дріб прирівняти до 0, за таким алгоритмом: .

4. Записати те коріння, яке вийшло в першому рівнянні і задовольняє другу нерівність, у відповідь.

Давайте розглянемо ще один приклад.

Приклад 2

Вирішити рівняння: .

Рішення

На самому початку перенесемо всі складові в ліву сторону, щоб праворуч залишився 0. Отримуємо:

Тепер наведемо ліву частину рівняння до спільного знаменника:

Дане рівняння еквівалентне системі:

Перше рівняння системи – це квадратне рівняння.

Коефіцієнти цього рівняння: . Обчислюємо дискримінант:

Отримуємо два корені: ; .

Тепер розв'яжемо другу нерівність: добуток множників не дорівнює 0 тоді і тільки тоді, коли жоден з множників не дорівнює 0.

Необхідно, щоб виконували дві умови: . Отримуємо, що з двох коренів першого рівняння підходить лише один – 3.

Відповідь:.

На цьому уроці ми згадали, що такий раціональний вираз, а також навчилися вирішувати раціональні рівняння, які зводяться до квадратних рівнянь.

На наступному уроці ми розглянемо раціональні рівняння моделі реальних ситуацій, а також розглянемо завдання на рух.

Список літератури

1. Башмаков М.І. Алгебра, 8 клас. - М: Просвітництво, 2004.
2. Дорофєєв Г.В., Суворова С.Б., Бунімович Є.А. та ін Алгебра, 8. 5-те вид. - М: Просвітництво, 2010.
3. Микільський С.М., Потапов М.А., Решетніков Н.М., Шевкін А.В. Алгебра, 8 клас. Підручник для загальноосвітніх установ. - М: Просвітництво, 2006.

1. Фестиваль педагогічних ідей "Відкритий урок" ().
2. School.xvatit.com ().
3. Rudocs.exdat.com ().

Домашнє завдання