Тригонометричні похідні приклади. III

Подано доказ і виведення формули для похідної синуса - sin(x). Приклади обчислення похідних від sin 2x, синуса у квадраті та кубі. Висновок формули для похідної синусу n-го порядку.

Похідна за змінною x від синуса x дорівнює косинусу x:
(sin x)′ = cos x.

Доведення

Для виведення формули похідної синуса ми скористаємося визначенням похідної:
.

Щоб знайти цю межу, нам потрібно перетворити вираз таким чином, щоб звести його до відомих законів, властивостей та правил. Для цього нам потрібно знати чотири властивості.
1) Значення першої чудової межі:
(1) ;
2) Безперервність функції косинус:
(2) ;
3) Тригонометричні формули. Нам знадобиться така формула:
(3) ;
4) Властивість меж:
Якщо і , то
(4) .

Застосовуємо ці правила до нашої межі. Спочатку перетворимо алгебраїчне вираз
.
Для цього застосуємо формулу
(3) .
У нашому випадку
; . Тоді
;
;
;
.

Тепер зробимо підстановку. При , . Застосуємо першу чудову межу (1):
.

Зробимо таку ж підстановку та використовуємо властивість безперервності (2):
.

Оскільки межі, обчислені вище, існують, то застосовуємо властивість (4):

.

Формула похідної синусу доведена.

Приклади

Розглянемо прості приклади знаходження похідних від функцій, які містять синус. Ми знайдемо похідні від наступних функцій:
y = sin 2x; y = sin 2 xта y = sin 3 x.

Приклад 1

Знайти похідну від sin 2x.

Рішення

Спочатку знайдемо похідну від найпростішої частини:
(2x) '= 2(x)' = 2 · 1 = 2.
Застосовуємо.
.
Тут.

Відповідь

(sin 2x) = 2 cos 2x.

Приклад 2

Знайти похідну від синуса в квадраті:
y = sin 2 x.

Рішення

Перепишемо вихідну функцію у більш зрозумілому вигляді:
.
Знайдемо похідну від найпростішої частини:
.
Застосовуємо формулу похідної складної функції.

.
Тут.

Можна застосувати одну із формул тригонометрії. Тоді
.

Відповідь

Приклад 3

Знайти похідну від синуса в кубі:
y = sin 3 x.

Похідні вищих порядків

Зауважимо, що похідну від sin xпершого порядку можна виразити через синус наступним чином:
.

Знайдемо похідну другого порядку, використовуючи формулу похідної складної функції:

.
Тут.

Тепер ми можемо помітити, що диференціювання sin xпризводить до збільшення його аргументу на . Тоді похідна n-го порядку має вигляд:
(5) .

Доведемо це, застосовуючи метод математичної індукції.

Ми вже перевірили, що при формула (5) справедлива.

Припустимо, що формула (5) справедлива за деякого значення . Доведемо, що з цього випливає, що формула (5) виконується для .

Випишемо формулу (5) при:
.
Диференціюємо це рівняння, застосовуючи правило диференціювання складної функції:

.
Тут.
Отже, ми знайшли:
.
Якщо підставити , то ця формула набуде вигляду (5).

Формулу доведено.

Для знаходження похідної тригонометричної функції потрібно користуватися таблицею похідних, А саме похідними 6-13.

При знаходженні похідних простих тригонометричних функцій щоб уникнути поширених помилок, слід звертати увагу на наступні моменти:

• у вираженні функції часто один із доданків є синус, косинус або іншу тригонометричну функціюнемає від аргументу функції, як від числа (константи), тому похідна цього доданка дорівнює нулю;
• майже завжди потрібно спростити вираз, отриманий у результаті диференціювання, а для цього потрібно впевнено користуватися знаннями з дій з дробами;
• Для спрощення виразу майже завжди потрібно знати тригонометричні тотожності, наприклад, формулу подвійного кута та формулу одиниці як суму квадратів синуса та косинуса.

приклад 1.Знайти похідну функції

Рішення. Допустимо, з похідної косинусавсе зрозуміло, скажуть багато хто, хто починає вивчати похідні. А як бути з похідної синусадванадцяти, поділених на пі? Відповідь: вважати рівною нулю! Тут синус (функція все-таки!) – пастка, тому що аргумент – не змінна ікс чи будь-яка інша змінна, а просто число. Тобто, синус цього числа теж число. А похідна числа (константи), як відомо з таблиці похідних, дорівнює нулю. Отже, залишаємо тільки мінус синус ікса і знаходимо його похідну, не забуваючи про знак:

.

приклад 2.Знайти похідну функції

.

Рішення. Другий доданок - той самий випадок, що і перший доданок у попередньому прикладі. Тобто число, а похідна числа дорівнює нулю. Знаходимо похідну другого доданку як похідну приватного:

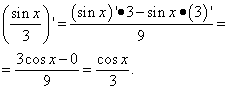
приклад 3.Знайти похідну функції

Рішення. Це вже інше завдання: тут у першому доданку немає ні арксинусу, ні іншої тригонометичної функції, але є ікс, отже це функція від ікса. Отже, диференціюємо її як доданок у сумі функцій:

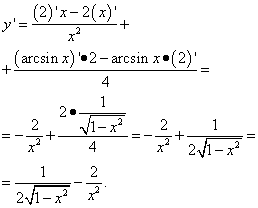
Тут були потрібні навички в діях з дробами, а саме - у ліквідації триповерховості дробу.

приклад 4.Знайти похідну функції

.

Рішення. Тут літера "фі" відіграє ту ж роль, що "ікс" у попередніх випадках (і в більшості інших, але не у всіх) - незалежної змінної. Тому, коли шукатимемо похідну твори функцій, не поспішатимемо оголошувати рівною нулю похідну кореня від "фі". Отже:

Але на цьому рішення не закінчується. Так як у двох дужках зібрані такі члени, від нас ще потрібно перетворити (спростити) вираз. Тому множимо дужки на винесені за них множники, а далі наводимо доданки до спільного знаменника і виконуємо інші елементарні перетворення:

Приклад 5.Знайти похідну функції

Рішення. У цьому прикладі від нас знадобиться той факт, що існує така тригонометрична функція - секанс - і її формули через косинус. Диференціюємо:

Приклад 6.Знайти похідну функції

.

Рішення. У цьому прикладі нам потрібно пам'ятати зі шкільного курсу формулу подвійного кута. Але спочатку диференціюємо:

,

(це і є формула подвійного кута)

При виведенні першої формули таблиці виходити з визначення похідної функції у точці. Візьмемо, де x- будь-яке дійсне число, тобто, x- Будь-яке число з області визначення функції. Запишемо межу відношення збільшення функції до збільшення аргументу при:

Слід зазначити, що під знаком межі виходить вираз, який не є невизначеністю нуль ділити на нуль, тому що в чисельнику знаходиться не нескінченно мала величина, а саме нуль. Іншими словами, збільшення постійної функції завжди дорівнює нулю.

Таким чином, похідна постійної функціїдорівнює нулю по всій області визначення.

Похідна статечної функції.

Формула похідної статечної функції має вигляд де показник ступеня p- Будь-яке дійсне число.

Доведемо спочатку формулу для натурального показника ступеня, тобто для p = 1, 2, 3, …

Будемо користуватися визначенням похідної. Запишемо межу відношення збільшення статечної функції до збільшення аргументу:

Для спрощення виразу в чисельнику звернемося до формули бінома Ньютона:

Отже,

Цим доведено формулу похідної статечної функції для натурального показника.

Похідна показової функції.

Висновок формули похідної наведемо на основі визначення:

Прийшли до невизначеності. Для її розкриття введемо нову змінну, причому при. Тоді. В останньому переході ми використали формулу переходу до нової основи логарифму.

Виконаємо підстановку у вихідну межу:

Якщо згадати другу чудову межу, то прийдемо до формули похідної показової функції:

Похідна логарифмічна функція.

Доведемо формулу похідної логарифмічної функції всім xв галузі визначення та всіх допустимих значеннях підстави aлогарифму. За визначенням похідної маємо:

Як Ви помітили, за доказом перетворення проводилися з використанням властивостей логарифму. Рівність справедливо з другого чудової межі.

Похідні тригонометричних функцій.

Для виведення формул похідних тригонометричних функцій нам доведеться згадати деякі формули тригонометрії, а також перша чудова межа.

За визначенням похідної для функції синуса маємо .

Скористаємося формулою різниці синусів:

Залишилося звернутися до першої чудової межі:

Таким чином, похідна функції sin xє cos x.

Абсолютно аналогічно доводиться формула похідної косинуса.

Отже, похідна функції cos xє -sin x.

Виведення формул таблиці похідних для тангенсу та котангенсу проведемо з використанням доведених правил диференціювання (похідна дробу).

Похідні гіперболічні функції.

Правила диференціювання та формула похідної показової функції з таблиці похідних дозволяють вивести формули похідних гіперболічного синуса, косинуса, тангенсу та котангенсу.

Похідна зворотної функції.

Щоб при викладі не було плутанини, давайте позначати в нижньому індексі аргумент функції, за яким виконується диференціювання, тобто це похідна функції f(x)по x.

Тепер сформулюємо правило знаходження похідної зворотної функції.

Нехай функції y = f(x)і x = g(y)взаємно зворотні, визначені на інтервалах та відповідно. Якщо у точці існує кінцева відмінна від нуля похідна функції f(x), то в точці існує кінцева похідна зворотної функції g(y), причому . В іншому записі .

Можна це правило переформулювати для будь-кого xз проміжку, тоді отримаємо .

Перевіримо справедливість цих формул.

Знайдемо зворотну функцію для натурального логарифму (тут y- функція, а x- Аргумент). Дозволивши це рівняння щодо x, отримаємо (тут x- функція, а y- Її аргумент). Тобто, та взаємно зворотні функції.

З таблиці похідних бачимо, що і .

Переконаємося, що формули знаходження похідних зворотної функції призводять нас до цих результатів:

Представлені похідні зворотних тригонометричних функцій та виведення їх формул. Також дано висловлювання похідних вищих порядків. Посилання на сторінки з докладнішим викладом виведення формул.

Спочатку виведемо формулу похідної арксинусу. Нехай
y = arcsin x.
Оскільки арксинус є функцією, зворотною до синуса, то
.
Тут y - функція від x. Диференціюємо по змінній x:
.
Застосовуємо:
.
Отже, ми знайшли:
.

Оскільки, то. Тоді
.
І попередня формула набуває вигляду:
. Звідси
.

Точно таким способом можна отримати формулу похідної арккосинусу. Однак простіше скористатися формулою, що зв'язує зворотні тригонометричні функції:
.
Тоді
.

Докладніше виклад представлено на сторінці “Виведення похідних арксинусу та арккосинусу”. Там дається виведення похідних двома способами- розглянутим вище та за формулою похідної зворотної функції.

Виведення похідних арктангенсу та арккотангенсу

У такий же спосіб знайдемо похідні арктангенсу та арккотангенсу.

Нехай
y = arctg x.
Арктангенс є функція, зворотна до тангенсу:
.
Диференціюємо по змінній x:
.
Застосовуємо формулу похідної складної функції:
.
Отже, ми знайшли:
.

Похідна арккотангенса:
.

Похідні арксинусу

Нехай
.
Похідну першого порядку від арксинусу ми вже знайшли:
.
Диференціюючи, знаходимо похідну другого порядку:
;
.
Її також можна записати у такому вигляді:
.
Звідси отримуємо диференціальне рівняння, якому задовольняють похідні арксинусу першого та другого порядків:
.

Диференціюючи це рівняння, можна знайти похідні найвищих порядків.

Похідна арксинусу n-го порядку

Похідна арксинуса n-го порядку має такий вигляд:
,
де - багаточлен ступеня. Він визначається за формулами:
;
.
Тут.

Багаточлен задовольняє диференціальне рівняння:
.

Похідна арккосинусу n-го порядку

Похідні для арккосинусу виходять із похідних для арксинусу за допомогою тригонометричної формули:
.
Тому похідні цих функцій відрізняються лише знаком:
.

Похідні арктангенсу

Нехай. Ми знайшли похідну арккотангенсу першого порядку:
.

Розкладемо дріб на найпростіші:

.
Тут - уявна одиниця, .

Диференціюємо раз і наводимо дріб до спільного знаменника:

.

Підставляючи , отримаємо:
.

Похідна арктангенса n-го порядку

Таким чином, похідну арктангенса n-го порядку можна уявити декількома способами:
;
.

Похідні арккотангенсу

Нехай тепер. Застосуємо формулу, що зв'язує зворотні тригонометричні функції:
.
Тоді похідна n-го порядку від арккотангенсу відрізняються лише знаком від похідної арктангенсу:
.

Підставивши, знайдемо:
.

Використана література:
Н.М. Гюнтер, Р.О. Кузьмін, Збірник завдань з вищої математики, "Лань", 2003.

Тема:«Похідна тригонометричних функцій».
Тип уроку- Урок закріплення знань.
Форма уроку- Інтегрований урок.
Місце уроку в системі уроків у цьому розділі- Узагальнюючий урок.
Цілі поставлені комплексно:

• навчальні:знати правила диференціювання, вміти застосовувати правила обчислення похідних під час вирішення рівнянь і нерівностей; удосконалювати предметні, у тому числі обчислювальні, уміння та навички; Навички роботи з комп'ютером;
• розвиваючі:розвиток інтелектуально-логічних умінь та пізнавальних інтересів;
• виховні:виховувати адаптивність до сучасних умов навчання.

Методи:

• репродуктивні та продуктивні;
• практичні та словесні;
• самостійні роботи;
• програмоване навчання, Т.С.О.;
• поєднання фронтальної, групової та індивідуальної роботи;
• диференційованого навчання;
• індуктивно-дедуктивний.

Форми контролю:

• усне опитування,
• програмований контроль,
• самостійна робота,
• індивідуальні завдання на комп'ютері,
• взаємоперевірка із застосуванням діагностичної карти учня.

ХІД УРОКУ

I. Організаційний момент

ІІ. Актуалізація опорних знань

а) Повідомлення цілей та завдань:

• знати правила диференціювання, вміти застосовувати правила обчислення похідних під час вирішення завдань, рівнянь та нерівностей;
• удосконалювати предметні, у тому числі обчислювальні, уміння та навички; Навички роботи з комп'ютером;
• розвивати інтелектуально-логічні вміння та пізнавальні інтереси;
• виховувати адаптивність до сучасних умов навчання.

б) Повторення навчального матеріалу

Правила обчислення похідних (повторення формул з комп'ютера зі звуковим супроводом). док.7.

1. Чому дорівнює похідна синуса?
2. Чому дорівнює похідна косинуса?
3. Чому дорівнює похідна тангенсу?
4. Чому дорівнює похідна котангенсу?

ІІІ. Усна робота

Обміняйтесь зошитами. Позначте в діагностичних картах правильно виконані завдання знаком +, а неправильно виконані завдання знаком –.

IV. Розв'язання рівнянь за допомогою похідної

- Як знайти точки, в яких похідна дорівнює нулю?

Щоб знайти точки, в яких похідна цієї функції дорівнює нулю, потрібно:

- Визначити характер функції,
- Визначити область визначення функції,
- Визначити похідну цієї функції,
- вирішити рівняння f "(x) = 0,
- Вибрати правильну відповідь.

Завдання 1.

Дано: у = х- sin x.
Знайти:точки, у яких похідна дорівнює нулю.
Рішення.Функція визначена і диференційована на множині всіх дійсних чисел, так як на множині всіх дійсних чисел визначені та диференційовані функції g(x) = xі t(x) = - sin x.
Використовуючи правила диференціювання, отримаємо f "(x) = (x- sin x)" = (x)" - ( sin x)" = 1 - cos x.
Якщо f "(x) = 0, то 1 - cos x = 0.
cos x= 1/; позбудемося ірраціональності в знаменнику, отримаємо cos x = /2.
За формулою t= ± arccos a+ 2n, n Z, отримаємо: х= ± arccos/2+2n, n Z.
Відповідь:х = ± /4 + 2n, n Z.

V. Розв'язання рівнянь за алгоритмом

Знайти, у яких точках перетворюється на нуль похідна.

Учень може вибрати будь-який із трьох прикладів. Перший приклад оцінюється оцінкою « 3 », другий – « 4 », третій – « 5 ». Рішення у зошитах з подальшою взаємоперевіркою. Один учень вирішує біля дошки. Якщо рішення виявляється неправильним, потрібно учневі повернутися до алгоритму і спробувати вирішити знову.

Програмований контроль.

Варіант 1		Варіант 2
y = 2х 3		y = 3х 2
y = 1/4 х 4 + 2х 2 – 7		y = 1/2 х 4 + 4х + 5
y = х 3 + 4х 2 – 3х. Вирішити рівняння y " = 0		y = 2х 3 – 9х 2 + 12х + 7. Вирішити рівняння y " = 0.
y= sin 2 х- cos 3 х.		y= cos 2 х- sin 3 х.
y= tg х- ctg ( х + /4).		y= ctg х+ tg ( х – /4).
y= sin 2 х.		y= cos 2 х.
Варіанти відповідей.
Останні матеріали розділу: