Praktiskt arbete: Transformation av grafer över funktioner. Derivat Geometrisk betydelse av derivata
Derivatan av en funktion $y = f(x)$ vid en given punkt $x_0$ är gränsen för förhållandet mellan ökningen av en funktion och motsvarande ökning av dess argument, förutsatt att den senare tenderar mot noll:
$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$
Differentiering är operationen att hitta derivatan.
Tabell över derivator av några elementära funktioner
| Fungera | Derivat |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^(n-1)$ |
| $(1)/(x)$ | $-(1)/(x^2)$ |
| $√x$ | $(1)/(2√x)$ |
| $e^x$ | $e^x$ |
| $lnx$ | $(1)/(x)$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $(1)/(cos^2x)$ |
| $ctgx$ | $-(1)/(sin^2x)$ |
Grundläggande regler för differentiering
1. Derivatan av summan (skillnaden) är lika med summan (skillnaden) av derivatorna
$(f(x) ± g(x))"= f"(x)±g"(x)$
Hitta derivatan av funktionen $f(x)=3x^5-cosx+(1)/(x)$
Derivatan av en summa (differens) är lika med summan (skillnad) av derivator.
$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$
2. Derivat av produkten
$(f(x) g(x)"= f"(x) g(x)+ f(x) g(x)"$
Hitta derivatan $f(x)=4x cosx$
$f"(x)=(4x)"·cosx+4x·(cosx)"=4·cosx-4x·sinx$
3. Derivat av kvoten
$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $
Hitta derivatan $f(x)=(5x^5)/(e^x)$
$f"(x)=((5x^5)"·e^x-5x^5·(e^x)")/((e^x)^2)=(25x^4·e^x- 5x^5 e^x)/((e^x)^2)$
4. Derivatan av en komplex funktion är lika med produkten av derivatan av den externa funktionen och derivatan av den interna funktionen
$f(g(x))"=f"(g(x)) g"(x)$
$f"(x)=cos"(5x)·(5x)"=-sin(5x)·5= -5sin(5x)$
Fysisk betydelse av derivatan
Om en materialpunkt rör sig rätlinjigt och dess koordinater ändras beroende på tid enligt lagen $x(t)$, så är den momentana hastigheten för denna punkt lika med derivatan av funktionen.
Punkten rör sig längs koordinatlinjen enligt lagen $x(t)= 1,5t^2-3t + 7$, där $x(t)$ är koordinaten vid tiden $t$. Vid vilken tidpunkt kommer punktens hastighet att vara lika med $12$?
1. Hastighet är derivatan av $x(t)$, så låt oss hitta derivatan av den givna funktionen
$v(t) = x"(t) = 1,5 2t -3 = 3t -3$
2. För att hitta vid vilken tidpunkt $t$ hastigheten var lika med $12$ skapar vi och löser ekvationen:
Geometrisk betydelse av derivata
Kom ihåg att ekvationen för en rät linje som inte är parallell med koordinataxlarna kan skrivas på formen $y = kx + b$, där $k$ är den räta linjens lutning. Koefficienten $k$ är lika med tangenten för lutningsvinkeln mellan den räta linjen och den positiva riktningen för $Ox$-axeln.
Derivatan av funktionen $f(x)$ i punkten $х_0$ är lika med lutningen $k$ för tangenten till grafen vid denna punkt:
Därför kan vi skapa en generell jämlikhet:
$f"(x_0) = k = tanα$
I figuren ökar tangenten till funktionen $f(x)$, därför koefficienten $k > 0$. Eftersom $k > 0$, då $f"(x_0) = tanα > 0$. Vinkeln $α$ mellan tangenten och den positiva riktningen $Ox$ är spetsig.
I figuren minskar tangenten till funktionen $f(x)$, därför minskar koefficienten $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
I figuren är tangenten till funktionen $f(x)$ parallell med $Ox$-axeln, därför är koefficienten $k = 0$, därför är $f"(x_0) = tan α = 0$. punkt $x_0$ där $f "(x_0) = 0$, anropas extremum.
Figuren visar en graf över funktionen $y=f(x)$ och en tangent till denna graf ritad vid punkten med abskissan $x_0$. Hitta värdet på derivatan av funktionen $f(x)$ vid punkten $x_0$.
Tangenten till grafen ökar, därför $f"(x_0) = tan α > 0$
För att hitta $f"(x_0)$ hittar vi tangenten för lutningsvinkeln mellan tangenten och den positiva riktningen för $Ox$-axeln. För att göra detta bygger vi tangenten till triangeln $ABC$.
Låt oss hitta tangenten för vinkeln $BAC$. (Tangensen för en spetsig vinkel i en rätvinklig triangel är förhållandet mellan den motsatta sidan och den intilliggande sidan.)
$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25 USD
$f"(x_0) = tg BAC = 0,25$
Svar: $0,25$
Derivaten används också för att hitta intervallen för ökande och minskande funktioner:
Om $f"(x) > 0$ på ett intervall, så ökar funktionen $f(x)$ på detta intervall.
Om $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
Figuren visar grafen för funktionen $y = f(x)$. Hitta bland punkterna $х_1,х_2,х_3...х_7$ de punkter där derivatan av funktionen är negativ.
Skriv ner antalet av dessa punkter som svar.
I uppgift nr 13 i Unified State Exam i matematik på grundläggande nivå måste du visa färdigheter och kunskap om ett av begreppen för en funktions beteende: derivator vid en punkt eller hastigheter för ökning eller minskning. Teorin för denna uppgift kommer att läggas till lite senare, men detta kommer inte att hindra oss från att i detalj undersöka flera typiska alternativ.
Analys av typiska alternativ för uppgifter nr 14 i Unified State Exam i matematik på grundläggande nivå
Alternativ 14MB1
Grafen visar temperaturens beroende av tid under uppvärmningsprocessen för en personbilsmotor. Den horisontella axeln visar tiden i minuter som har gått sedan motorn startade; på den vertikala axeln är motortemperaturen i grader Celsius.

Använd grafen för att matcha varje tidsintervall med egenskaperna för motoruppvärmningsprocessen under detta intervall.
I tabellen, under varje bokstav, ange motsvarande nummer.
Exekveringsalgoritm:
- Välj det tidsintervall under vilket temperaturen sjunkit.
- Sätt på en linjal på 30°C och bestäm tidsintervallet under vilket temperaturen var under 30°C.
Lösning:
Låt oss välja det tidsintervall under vilket temperaturen sjönk. Denna sektion är synlig för blotta ögat, den börjar 8 minuter från det att motorn startar.
Sätt på en linjal på 30°C och bestäm tidsintervallet under vilket temperaturen var under 30°C.

Under linjalen kommer det att finnas en sektion som motsvarar tidsintervallet 0 - 1 min.
Med hjälp av en penna och en linjal hittar vi vid vilket tidsintervall temperaturen låg i intervallet från 40°C till 80°C.
Låt oss släppa vinkelräta från punkterna som motsvarar 40°С och 80°С på grafen, och från de resulterande punkterna sänker vi vinkelräta på tidsaxeln.

Vi ser att detta temperaturintervall motsvarar ett tidsintervall på 3 – 6,5 minuter. Det vill säga från de som ges i villkoret 3 – 6 minuter.
Med hjälp av elimineringsmetoden kommer vi att välja alternativet som saknas svar.
Alternativ 14MB2
Lösning:
Låt oss analysera grafen för funktion A. Om funktionen ökar så är derivatan positiv och vice versa. Funktionens derivata är lika med noll vid extrempunkterna.
Först ökar funktion A, d.v.s. derivatan är positiv. Detta motsvarar graferna för derivatorna 2 och 3. Vid maxpunkten för funktionen x = -2, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta tillstånd motsvarar graf nummer 3.
Först minskar funktion B, d.v.s. derivatan är negativ. Detta motsvarar graferna för derivatorna 1 och 4. Funktionens maximala punkt är x=-2, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta villkor motsvarar graf nummer 4.
Först ökar funktion B, d.v.s. derivatan är positiv. Detta motsvarar graferna för derivatorna 2 och 3. Funktionens maximala punkt är x = 1, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta tillstånd motsvarar graf nummer 2.
Med hjälp av elimineringsmetoden kan vi bestämma att grafen för funktionen Г motsvarar grafen för derivatan numrerad 1.
Svar: 3421.
Alternativ 14MB3
Exekveringsalgoritm för varje funktion:
- Bestäm intervallen för ökande och minskande funktioner.
- Bestäm max- och minimumpunkterna för funktioner.
- Dra slutsatser och matcha de föreslagna graferna.
Lösning:
Låt oss analysera grafen för funktion A.
Om funktionen ökar är derivatan positiv och vice versa. Funktionens derivata är lika med noll vid extrempunkterna.
Extremumpunkten är den punkt där funktionens maximala eller lägsta värde uppnås.
Först ökar funktion A, d.v.s. derivatan är positiv. Detta motsvarar graferna för derivatorna 3 och 4. Vid maxpunkten för funktionen x=0, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta villkor motsvarar graf nummer 4.
Låt oss analysera grafen för funktion B.
Först minskar funktion B, d.v.s. derivatan är negativ. Detta motsvarar graferna för derivatorna 1 och 2. Minimipunkten för funktionen är x=-1, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta tillstånd motsvarar graf nummer 2.
Låt oss analysera grafen för funktion B.
Först minskar funktion B, d.v.s. derivatan är negativ. Detta motsvarar graferna för derivatorna 1 och 2. Minimipunkten för funktionen är x = 0, det vill säga vid denna punkt ska derivatan vara lika med noll. Detta tillstånd motsvarar graf nummer 1.
Med hjälp av elimineringsmetoden kan vi bestämma att grafen för funktionen Г motsvarar grafen för derivatan numrerad 3.
Svar: 4213.
Alternativ 14MB4
Figuren visar grafen för funktionen och tangenterna ritade till den vid abskisspunkterna A, B, C och D.Den högra kolumnen visar värdena för derivatan vid punkterna A, B, C och D. Använd grafen för att matcha varje punkt med värdet på derivatan av funktionen i den.

POÄNG
A
I
MED
D
DERIVATVÄRDEN
1) –4
2) 3
3) 2/3
4) -1/2
Låt oss komma ihåg vad derivatan betyder, nämligen dess värde vid en punkt - värdet av derivatfunktionen i en punkt är lika med tangenten för tangentens lutningsvinkel (koefficient).
I svaren har vi två positiva och två negativa alternativ. Som vi minns, om koefficienten är rak (grafik y = kx+ b) är positiv ökar linjen, men om den är negativ så minskar linjen.
Vi har två ökande linjer - vid punkterna A och D. Låt oss nu komma ihåg vad värdet på koefficienten k betyder?
Koefficienten k visar hur snabbt funktionen ökar eller minskar (i själva verket är koefficienten k själv en derivata av funktionen y = kx+ b).
Därför motsvarar k = 2/3 en plattare rät linje - D, och k = 3 - A.
Detsamma gäller för negativa värden: punkt B motsvarar en brantare rät linje med k = - 4, och punkt C - -1/2.
Alternativ 14MB5
Prickarna i figuren visar de månatliga försäljningsvolymerna för värmare i en hushållsbutik. Månaderna anges horisontellt och antalet värmare som säljs vertikalt. För tydlighetens skull är punkterna förbundna med en linje.

Använd figuren och matcha var och en av de angivna tidsperioderna med egenskaperna för värmeförsäljningen.

Exekveringsalgoritm
Vi analyserar delar av grafen som motsvarar olika årstider. Vi formulerar de situationer som visas på grafen. Vi hittar de mest lämpliga svaren för dem.
Lösning:
Vintertid översteg antalet försäljningar 120 enheter/månad och det ökade hela tiden. Denna situation motsvarar svarsalternativ nr 3. De där. vi får: A–3.
Under våren sjönk försäljningen successivt från 120 värmare per månad till 50. Närmast denna formulering är alternativ nr 2. Vi har: B–2.
På sommaren förändrades inte antalet försäljningar och var minimalt. Den 2:a delen av denna formulering återspeglas inte i svaren, och endast nr 4 är lämplig för den första. Härifrån har vi: AT 4.
Under hösten växte försäljningen, men antalet översteg på ingen månad 100 enheter. Denna situation beskrivs i alternativ nr 1. Vi får: G–1.
Alternativ 14MB6
Grafen visar beroendet av hastigheten på en vanlig buss i tid. Den vertikala axeln visar bussens hastighet i km/h och den horisontella axeln visar tiden i minuter sedan bussen började röra sig.

Använd grafen för att matcha varje tidsintervall med egenskaperna för bussrörelsen under detta intervall.

Exekveringsalgoritm
- Vi bestämmer delningspriset på den horisontella och vertikala skalan.
- Vi analyserar i sin tur de föreslagna påståendena 1–4 från den högra kolumnen (”Kännetecken”). Vi jämför dem med tidsintervall från den vänstra kolumnen i tabellen och hittar "bokstav-tal"-par för svaret.
Lösning:
Den horisontella skalindelningen är 1 s, den vertikala skalan är 20 km/h.
- När bussen stannar är dess hastighet 0. Bussen hade noll hastighet under 2 minuter i rad endast från den 9:e till den 11:e minuten. Denna tid ligger inom intervallet 8–12 minuter. Så vi har ett par för svaret: B–1.
- Bussen hade en hastighet på 20 km/h eller mer under flera perioder. Dessutom är alternativ A inte lämpligt här, eftersom till exempel hastigheten i den 7:e minuten var 60 km/h, alternativ B - eftersom det redan har tillämpats, alternativ D - eftersom bussen i början och slutet av intervallet hade noll hastighet. I detta fall är alternativ B (12–16 min) lämpligt; Under detta intervall börjar bussen röra sig med en hastighet av 40 km/h, accelererar sedan till 100 km/m och minskar sedan gradvis hastigheten till 20 km/h. Så vi har: AT 2.
- Det finns en hastighetsbegränsning här. Samtidigt överväger vi inte alternativ B och C. De återstående intervallen A och D är båda lämpliga. Därför skulle det vara korrekt att överväga det 4:e alternativet först och sedan återgå till det 3:e.
- Av de två återstående intervallen är endast 4–8 minuter lämpliga för karaktäristik nr 4, eftersom det blev stopp under detta intervall (vid 6:e minuten). Det fanns inga stopp mellan 18 och 22 minuter. Vi får: A–4. Det följer att för egenskap nr 3 måste du ta intervallet Г, dvs. det visar sig vara ett par G–3.
Alternativ 14MB7
Prickarna i figuren visar Kinas befolkningstillväxt mellan 2004 och 2013. Den horisontella linjen anger året, den vertikala linjen anger befolkningstillväxten i procent (befolkningsökning i förhållande till föregående år). För tydlighetens skull är punkterna förbundna med en linje.
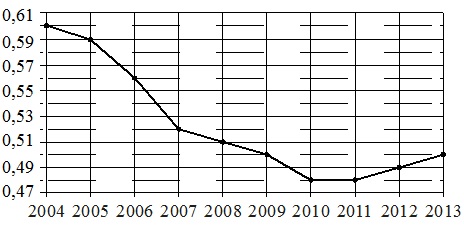
Använd figuren och matcha var och en av de angivna tidsperioderna med egenskaperna hos Kinas befolkningstillväxt under denna period.

Exekveringsalgoritm
- Vi bestämmer priset för att dividera den vertikala skalan av ritningen. Det finns som skillnaden mellan ett par intilliggande skalvärden, dividerat med 2 (eftersom det finns 2 divisioner mellan två intilliggande värden).
- Vi analyserar sekventiellt egenskaperna 1–4 som ges i villkoret (vänster tabellkolumn). Vi jämför var och en av dem med en viss tidsperiod (höger tabellkolumn).
Lösning:
Värdet för vertikal skaldelning är 0,01 %.
- Nedgången i tillväxt fortsatte kontinuerligt från 2004 till 2010. 2010–2011 var ökningen genomgående minimal och från och med 2012 började den öka. De där. tillväxten stoppades 2010. Detta år är under perioden 2009–2011. Följaktligen har vi: I 1.
- Den största nedgången i tillväxt bör betraktas som den brantaste fallande linjen i grafen i figuren. Den infaller under perioden 2006–2007. och är 0,04 % per år (0,59–0,56=0,04 % 2006 och 0,56–0,52=0,04 % 2007). Härifrån får vi: A–2.
- Tillväxten som anges i egenskap nr 3 började 2007, fortsatte 2008 och slutade 2009. Detta motsvarar tidsperiod B, dvs. vi har: B–3.
- Befolkningstillväxten började öka efter 2011, d.v.s. 2012–2013 Därför får vi: G–4.
Alternativ 14MB8
Figuren visar grafen för funktionen och tangenterna ritade till den vid punkter med abskissorna A, B, C och D.

Den högra kolumnen visar värdena för derivatan av funktionen vid punkterna A, B, C och D. Använd grafen för att matcha varje punkt med värdet på funktionens derivata i den.

Exekveringsalgoritm
- Vi betraktar ett tangentpar som har en spetsig vinkel med x-axelns positiva riktning. Vi jämför dem och hittar en matchning mellan paret av motsvarande derivata värden.
- Vi betraktar ett par tangenter som bildar en trubbig vinkel med x-axelns positiva riktning. Vi jämför dem modulo och bestämmer deras överensstämmelse med värdena på derivaten bland de två återstående i den högra kolumnen.
Lösning:
En spetsig vinkel med abskissaxelns positiva riktning bildas av derivator i T.B och T.S. Dessa derivat har positiva värden. Därför bör du här välja mellan värden nr 1 och 3. Genom att tillämpa regeln att om vinkeln är mindre än 45 0, så är derivatan mindre än 1, och om den är mer, så är den mer än 1, vi drar slutsatsen: i punkt B är moduloderivatan större än 1, i t.C – mindre än 1. Det betyder att du kan göra par för svaret: VID 3 Och S–1.
Derivaterna i t.A och t.D bildar en trubbig vinkel med abskissaxelns positiva riktning. Och här tillämpar vi samma regel och parafraserar den lite: ju mer tangenten i en punkt "trycks" mot x-axelns linje (mot dess negativa riktning), desto större är dess modul. Då får vi: derivatan i t.A är mindre i absolut värde än derivatan i t.D. Härifrån har vi par för svaret: A–2 Och D–4.
Alternativ 14MB9
Prickarna i figuren visar den genomsnittliga dagliga lufttemperaturen i Moskva i januari 2011. Månadens datum anges horisontellt, och temperaturen i grader Celsius anges vertikalt. För tydlighetens skull är punkterna förbundna med en linje.

Använd figuren och matcha var och en av de angivna tidsperioderna med den karakteristiska temperaturförändringen.

Exekveringsalgoritm
Vi analyserar egenskaperna 1–4 (höger kolumn) sekventiellt med hjälp av grafen i figuren. Vi tilldelar var och en av dem till en viss tidsperiod (vänster kolumn).
Lösning:
- En ökning av temperaturen observerades först i slutet av perioden 22–28 januari. Här den 27 och 28 ökade det med 1 respektive 2 grader. I slutet av perioden 1–7 januari var temperaturen stabil (–10 grader), i slutet av 8–14 och 15–21 januari sjönk den (från –1 till –2 och från –11 till –12 grader , respektive). Därför får vi: G–1.
- Eftersom varje tidsperiod omfattar 7 dagar måste temperaturen analyseras från och med den 4:e dagen i varje period. Temperaturen förblev konstant i 3–4 dagar endast från 4 januari till 7 januari. Därför får vi svaret: A–2.
- Den månatliga lägsta temperaturen observerades den 17 januari. Detta antal faller inom perioden 15–21 januari. Härifrån har vi ett par: VID 3.
- Temperaturmaximum inträffade den 10 januari och var +1 grad. Detta datum infaller mellan 8–14 januari. Så vi har: B–4.
Alternativ 14MB10
Exekveringsalgoritm
- Funktionens värde vid en punkt är positivt om denna punkt är placerad ovanför Ox-axeln.
- Derivatan i en punkt är större än noll om tangenten till denna punkt bildar en spetsig vinkel med Ox-axelns positiva riktning.
Lösning:
Punkt A. Den ligger under Ox-axeln, vilket betyder att värdet på funktionen i den är negativt. Om du ritar en tangent i den, så blir vinkeln mellan den och den positiva riktningen Ox cirka 90 0, d.v.s. bildar en spetsig vinkel. Detta innebär att egenskap nr 3 är lämplig i detta fall. De där. vi har: A–3.
Punkt B. Den ligger ovanför Ox-axeln, dvs. punkten har ett positivt värde av funktionen. Tangenten vid denna punkt kommer att vara ganska nära x-axeln och bildar en trubbig vinkel (något mindre än 180 0) med dess positiva riktning. Följaktligen är derivatan vid denna punkt negativ. Här passar alltså egenskap 1. Vi får svaret: I 1.
Punkt C. Punkten ligger under Ox-axeln, tangenten vid den bildar en stor trubbig vinkel med x-axelns positiva riktning. De där. i t.C är värdet på både funktionen och derivatan negativt, vilket motsvarar egenskap nr 2. Svar: S–2.
Punkt D. Punkten ligger ovanför Ox-axeln, och tangenten vid den bildar en spetsig vinkel med axelns positiva riktning. Detta tyder på att både värdet på funktionen och värdet på derivatan här är större än noll. Svar: D–4.
Alternativ 14MB11
Prickarna i figuren visar de månatliga försäljningsvolymerna för kylskåp i en hushållsbutik. Månaderna anges horisontellt och antalet kylskåp som säljs vertikalt. För tydlighetens skull är punkterna förbundna med en linje.

Använd figuren och matcha var och en av de angivna tidsperioderna med egenskaperna för försäljning av kylskåp.
Den räta linjen y=3x+2 är tangent till grafen för funktionen y=-12x^2+bx-10. Hitta b, givet att abskissan för tangentpunkten är mindre än noll.
Visa lösningLösning
Låt x_0 vara abskissan för den punkt på grafen för funktionen y=-12x^2+bx-10 genom vilken tangenten till denna graf passerar.
Värdet på derivatan vid punkten x_0 är lika med lutningen på tangenten, det vill säga y"(x_0)=-24x_0+b=3. Å andra sidan hör tangenspunkten samtidigt till både grafen för funktion och tangenten, det vill säga -12x_0^2+bx_0-10= 3x_0 + 2. Vi får ett ekvationssystem \begin(cases) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end(fall)
När vi löser detta system får vi x_0^2=1, vilket betyder antingen x_0=-1 eller x_0=1. Enligt abskissvillkoret är tangentpunkterna mindre än noll, så x_0=-1, då b=3+24x_0=-21.
Svar
Skick
Figuren visar en graf över funktionen y=f(x) (som är en streckad linje som består av tre raka segment). Använd figuren och beräkna F(9)-F(5), där F(x) är en av antiderivatorna av funktionen f(x).
Visa lösningLösning
Enligt Newton-Leibniz-formeln är skillnaden F(9)-F(5), där F(x) är en av antiderivaten av funktionen f(x), lika med arean av den krökta trapetsen begränsade genom grafen för funktionen y=f(x), räta linjer y=0 , x=9 och x=5. Från grafen bestämmer vi att den angivna krökta trapetsen är en trapets med baser lika med 4 och 3 och höjd 3.
Dess yta är lika stor \frac(4+3)(2)\cdot 3=10.5.
Svar
Källa: ”Matematik. Förberedelse för Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Skick
Figuren visar en graf av y=f"(x) - derivatan av funktionen f(x), definierad på intervallet (-4; 10). Hitta intervallen för minskande funktion f(x). I ditt svar, ange längden på den största av dem.

Lösning
Som bekant minskar funktionen f(x) på de intervall vid varje punkt där derivatan f"(x) är mindre än noll. Med tanke på att det är nödvändigt att hitta längden på den största av dem, är tre sådana intervall naturligt särskiljd från figuren: (-4; -2); (0; 3); (5; 9).
Längden på den största av dem - (5; 9) är 4.
Svar
Källa: ”Matematik. Förberedelse för Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Skick
Figuren visar en graf av y=f"(x) - derivatan av funktionen f(x), definierad på intervallet (-8; 7). Hitta antalet maxpunkter för funktionen f(x) som hör till intervallet [-6; -2].
.png)
Lösning
Grafen visar att derivatan f"(x) av funktionen f(x) ändrar tecken från plus till minus (vid sådana punkter kommer det att finnas ett maximum) vid exakt en punkt (mellan -5 och -4) från intervallet [ -6; -2 ] Därför finns det på intervallet [-6; -2] exakt en maxpunkt.
Svar
Källa: ”Matematik. Förberedelse för Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Skick
Figuren visar en graf över funktionen y=f(x), definierad på intervallet (-2; 8). Bestäm antalet punkter där derivatan av funktionen f(x) är lika med 0.

Lösning
Likheten för derivatan vid en punkt till noll betyder att tangenten till grafen för funktionen som ritas vid denna punkt är parallell med Ox-axeln. Därför hittar vi punkter där tangenten till grafen för funktionen är parallell med Ox-axeln. På det här diagrammet är sådana punkter extrema punkter (högsta eller lägsta punkter). Som du kan se finns det 5 extrema punkter.
Svar
Källa: ”Matematik. Förberedelse för Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Skick
Den räta linjen y=-3x+4 är parallell med tangenten till grafen för funktionen y=-x^2+5x-7. Hitta abskissan för tangentpunkten.
Visa lösningLösning
Vinkelkoefficienten för den räta linjen till grafen för funktionen y=-x^2+5x-7 vid en godtycklig punkt x_0 är lika med y"(x_0). Men y"=-2x+5, vilket betyder y" (x_0)=-2x_0+5. Vinkel koefficienten för linjen y=-3x+4 som anges i villkoret är lika med -3. Parallella linjer har samma lutningskoefficienter. Därför hittar vi ett värde x_0 så att =- 2x_0 +5=-3.
Vi får: x_0 = 4.
Svar
Källa: ”Matematik. Förberedelse för Unified State Exam 2017. Profilnivå." Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Skick
Figuren visar en graf över funktionen y=f(x) och punkterna -6, -1, 1, 4 är markerade på abskissan. Vid vilken av dessa punkter är derivatan minst? Ange denna punkt i ditt svar.






















































 Tillbaka framåt
Tillbaka framåt
Uppmärksamhet! Förhandsvisningar av bilder är endast i informationssyfte och representerar kanske inte alla funktioner i presentationen. Om du är intresserad av detta arbete, ladda ner den fullständiga versionen.
Lektionstyp: upprepning och generalisering.
Lektionsformat: lektions-konsultation.
Lektionens mål:
- pedagogisk: upprepa och generalisera teoretisk kunskap om ämnena: "Geometrisk betydelse av derivatan" och "Tillämpning av derivatan för studier av funktioner"; överväga alla typer av B8-problem som man stöter på vid Unified State Examination i matematik; ge eleverna möjlighet att testa sina kunskaper genom att lösa problem självständigt; lära ut hur man fyller i provsvarsformuläret;
- utvecklande: att främja utvecklingen av kommunikation som en metod för vetenskaplig kunskap, semantiskt minne och frivillig uppmärksamhet; bildandet av sådana nyckelkompetenser som jämförelse, sammanställning, klassificering av objekt, fastställande av adekvata sätt att lösa en pedagogisk uppgift baserat på givna algoritmer, förmågan att agera självständigt i osäkerhetssituationer, övervaka och utvärdera ens aktiviteter, hitta och eliminera orsakerna av svårigheter;
- pedagogisk: utveckla elevernas kommunikativa kompetens (kommunikationskultur, förmåga att arbeta i grupp); främja utvecklingen av behovet av egenutbildning.
Teknik: utvecklingsutbildning, IKT.
Lär ut metoder: verbala, visuella, praktiska, problematiska.
Arbetsformer: individuell, frontal, grupp.
Utbildnings- och metodstöd:
1. Algebra och början av matematisk analys 11:e klass: lärobok. För allmänbildning Institutioner: grundläggande och profil. nivåer / (Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin); redigerad av A. B. Zhizhchenko. – 4:e uppl. – M.: Utbildning, 2011.
2. Unified State Exam: 3000 problem med svar i matematik. Alla uppgifter i grupp B/A.L. Semenov, I.V. Jasjtjenko och andra; redigerad av A.L. Semyonova, I.V. Jasjtjenko. – M.: Förlaget "Exam", 2011.
3. Öppna uppgiftsbanken.
Utrustning och material för lektionen: projektor, skärm, PC för varje elev med en presentation installerad på, utskrift av PM till alla elever (Bilaga 1) och resultatlista ( Bilaga 2) .
Preliminära förberedelser inför lektionen: som läxa ombeds eleverna att upprepa teoretiskt material från läroboken om ämnena: "Geometrisk betydelse av derivatan", "Tillämpning av derivatan för att studera funktioner"; Klassen är indelad i grupper (4 personer vardera), i var och en av dem finns elever på olika nivåer.
Lektionsförklaring: Den här lektionen lärs ut i 11:e klass vid upprepningsstadiet och förberedelserna för Unified State Exam. Lektionen syftar till att repetera och generalisera teoretiskt material, att tillämpa det på att lösa tentamensproblem. Lektionens längd - 1,5 timmar .
Den här lektionen är inte kopplad till läroboken, så den kan undervisas samtidigt som du arbetar med alla läromedel. Denna lektion kan också delas upp i två separata och ges som sista lektioner i de ämnen som tas upp.
Under lektionerna
I. Organisatoriskt ögonblick.
II. Lektion att sätta upp mål.
III. Upprepning om ämnet "Geometrisk betydelse av derivator."
Muntligt frontalt arbete med projektor (slides nr 3-7)
Arbeta i grupp: lösa problem med tips, svar, med lärarkonsultation (bilder nr 8-17)
IV. Självständigt arbete 1.
Eleverna arbetar individuellt på en PC (bilder nr 18-26) och skriver in sina svar i utvärderingsbladet. Vid behov kan du konsultera en lärare, men i det här fallet kommer eleven att förlora 0,5 poäng. Om eleven slutför arbetet tidigare kan denne välja att lösa ytterligare uppgifter från samlingen, s. 242, 306-324 (ytterligare uppgifter bedöms separat).
V. Ömsesidig verifiering.
Studenter utbyter bedömningsblad, kontrollerar en väns arbete och tilldelar poäng (bild nr 27)
VI. Korrigering av kunskap.
VII. Upprepning på ämnet "Tillämpning av derivatan för att studera funktioner"
Muntligt frontalt arbete med projektor (slides nr 28-30)
Arbeta i grupp: lösa problem med tips, svar, med lärarkonsultation (bilder nr 31-33)
VIII. Självständigt arbete 2.
Eleverna arbetar individuellt på en PC (bild nr 34-46), och anger sina svar på svarsformuläret. Vid behov kan du konsultera en lärare, men i det här fallet kommer eleven att förlora 0,5 poäng. Om eleven slutför arbetet tidigare kan denne välja att lösa ytterligare uppgifter ur samlingen, s. 243-305 (ytterligare uppgifter bedöms separat).
IX. Peer review.
Elever utbyter bedömningsblad, kontrollerar sin väns arbete och tilldelar poäng (bild nr 47).
X. Korrigering av kunskap.
Eleverna arbetar igen i sina grupper, diskuterar lösningen och rättar till misstag.
XI. Sammanfattande.
Varje elev räknar ut sina poäng och sätter ett betyg på poängbladet.
Eleverna lämnar till läraren ett bedömningsblad och lösningar på ytterligare problem.
Varje elev får ett memo (bild nr 53-54).
XII. Reflexion.
Eleverna uppmanas att utvärdera sina kunskaper genom att välja en av fraserna:
- Jag lyckades!!!
- Vi måste lösa ytterligare ett par exempel.
- Ja, vem kom på den här matematiken!
XIII. Läxa.
För läxor ombeds eleverna att välja uppgifter från samlingen, s. 242-334, samt från en öppen uppgiftsbank.
Försök först att hitta funktionens domän:
Klarade du dig? Låt oss jämföra svaren:
Är allt rätt? Bra gjort!
Låt oss nu försöka hitta intervallet av värden för funktionen:

Hittades? Låt oss jämföra:
Jag fattar? Bra gjort!
Låt oss arbeta med grafer igen, bara nu är det lite mer komplicerat - hitta både definitionsdomänen för funktionen och funktionens värdeintervall.
Hur man hittar både domänen och intervallet för en funktion (avancerat)

Här är vad som hände:
Jag tror att du har listat ut graferna. Låt oss nu försöka hitta definitionsdomänen för en funktion i enlighet med formlerna (om du inte vet hur man gör detta, läs avsnittet om):
Klarade du dig? Låt oss kolla svarar:
- , eftersom det radikala uttrycket måste vara större än eller lika med noll.
- , eftersom du inte kan dividera med noll och det radikala uttrycket inte kan vara negativt.
- , eftersom, respektive, för alla.
- , eftersom du inte kan dividera med noll.
Men vi har fortfarande en fråga obesvarad...
Jag kommer att upprepa definitionen en gång till och betona den:
Märkte du? Ordet "singel" är en mycket, mycket viktig del av vår definition. Jag ska försöka förklara det för dig med fingrarna.
Låt oss säga att vi har en funktion definierad av en rät linje. . Vid ersätter vi detta värde i vår "regel" och får det. Ett värde motsvarar ett värde. Vi kan till och med göra en tabell över de olika värdena och rita upp denna funktion för att se själva.
"Se! - du säger, "" inträffar två gånger!" Så kanske en parabel inte är en funktion? Nej det är!
Det faktum att " " dyker upp två gånger är ingen anledning att anklaga parabeln för tvetydighet!
Faktum är att vi, när vi räknade för, fick en match. Och när vi räknade med fick vi ett spel. Så det stämmer, en parabel är en funktion. Titta på grafen:

Jag fattar? Om inte, här är ett livsexempel som är väldigt långt ifrån matematik!
Låt oss säga att vi har en grupp sökande som träffades när de skickade in dokument, som var och en berättade i en konversation där han bor:

Håller med, det är fullt möjligt för flera killar att bo i en stad, men det är omöjligt för en person att bo i flera städer samtidigt. Detta är som en logisk representation av vår "parabel" - Flera olika X motsvarar samma spel.
Låt oss nu komma med ett exempel där beroendet inte är en funktion. Låt oss säga att samma killar berättade för oss vilka specialiteter de sökte:

Här har vi en helt annan situation: en person kan enkelt lämna in dokument för en eller flera riktningar. Det är ett element uppsättningar sätts i korrespondens flera element mängder. Respektive, detta är inte en funktion.
Låt oss testa dina kunskaper i praktiken.
Bestäm utifrån bilderna vad som är en funktion och vad som inte är det:

Jag fattar? Och här är den svarar:
- Funktionen är - B, E.
- Funktionen är inte - A, B, D, D.
Du frågar varför? Ja, här är varför:

På alla bilder utom I) Och E) Det finns flera för en!
Jag är säker på att du nu enkelt kan skilja en funktion från en icke-funktion, säga vad ett argument är och vad en beroende variabel är, och även bestämma intervallet för tillåtna värden för ett argument och definitionsintervallet för en funktion . Låt oss gå vidare till nästa avsnitt - hur ställer man in en funktion?
Metoder för att specificera en funktion
Vad tror du att orden betyder? "ställ in funktion"? Det stämmer, det innebär att förklara för alla vilken funktion vi pratar om i det här fallet. Förklara det dessutom på ett sådant sätt att alla förstår dig rätt och funktionsgraferna som ritats av människor baserat på din förklaring är desamma.
Hur kan jag göra det? Hur ställer man in en funktion? Den enklaste metoden, som redan har använts mer än en gång i den här artikeln, är med hjälp av formeln. Vi skriver en formel och genom att ersätta ett värde i den, beräknar vi värdet. Och som ni minns är en formel en lag, en regel genom vilken det blir tydligt för oss och för en annan person hur ett X förvandlas till ett Y.
Vanligtvis är det precis vad de gör - i uppgifter ser vi färdiga funktioner specificerade av formler, men det finns andra sätt att ställa in en funktion som alla glömmer, och därför frågan "hur kan du annars ställa in en funktion?" bafflar. Låt oss förstå allt i ordning, och låt oss börja med den analytiska metoden.
Analytisk metod för att specificera en funktion
Den analytiska metoden är att specificera en funktion med hjälp av en formel. Detta är den mest universella, heltäckande och entydiga metoden. Om du har en formel, då vet du absolut allt om en funktion - du kan göra en värdetabell av den, du kan bygga en graf, bestämma var funktionen ökar och var den minskar, i allmänhet, studera den i sin helhet.
Låt oss överväga funktionen. Vad är skillnaden?
"Vad betyder det?" - du frågar. Jag ska förklara nu.
Låt mig påminna er om att uttrycket inom parentes i notationen kallas för ett argument. Och detta argument kan vara vilket uttryck som helst, inte nödvändigtvis enkelt. Följaktligen, oavsett argumentet (uttrycket inom parentes) kommer vi att skriva det istället i uttrycket.
I vårt exempel kommer det att se ut så här:
Låt oss överväga en annan uppgift relaterad till den analytiska metoden för att specificera en funktion, som du kommer att ha på provet.
Hitta värdet på uttrycket vid.
Jag är säker på att du först blev rädd när du såg ett sådant uttryck, men det är absolut inget läskigt med det!
Allt är detsamma som i föregående exempel: oavsett argumentet (uttrycket inom parentes) kommer vi att skriva det istället i uttrycket. Till exempel för en funktion.
Vad behöver göras i vårt exempel? Istället måste du skriva, och istället -:
förkorta det resulterande uttrycket:
Det är allt!
Självständigt arbete
Försök nu själv hitta innebörden av följande uttryck:
- , Om
- , Om
Klarade du dig? Låt oss jämföra våra svar: Vi är vana vid att funktionen har formen
Även i våra exempel definierar vi funktionen på exakt detta sätt, men analytiskt går det till exempel att specificera funktionen i implicit form.
Testa att bygga den här funktionen själv.
Klarade du dig?
Så här byggde jag det.
Vilken ekvation härledde vi till slut?
Höger! Linjär, vilket betyder att grafen blir en rak linje. Låt oss göra en tabell för att avgöra vilka punkter som hör till vår linje:
Det var precis det vi pratade om... En motsvarar flera.
Låt oss försöka rita vad som hände:

Är det vi har en funktion?
Det stämmer, nej! Varför? Försök att svara på denna fråga med hjälp av en ritning. Vad fick du?

"Eftersom ett värde motsvarar flera värden!"
Vilken slutsats kan vi dra av detta?
Det stämmer, en funktion kan inte alltid uttryckas explicit, och det som är "förklädd" som en funktion är inte alltid en funktion!
Tabellform för att specificera en funktion
Som namnet antyder är denna metod ett enkelt tecken. Jaja. Som den du och jag redan har gjort. Till exempel:
Här märkte du omedelbart ett mönster - Y:et är tre gånger större än X:et. Och nu uppgiften att "tänka mycket noga": tror du att en funktion som ges i form av en tabell är likvärdig med en funktion?
Låt oss inte prata på länge, men låt oss rita!
Så. Vi ritar funktionen som anges av tapeten på följande sätt:

Ser du skillnaden? Allt handlar inte om de markerade poängen! Ta en närmare titt:

Har du sett den nu? När vi definierar en funktion i tabellform visar vi på grafen endast de punkter som vi har i tabellen och linjen (som i vårt fall) passerar endast genom dem. När vi definierar en funktion analytiskt kan vi ta vilka punkter som helst, och vår funktion är inte begränsad till dem. Detta är egenheten. Kom ihåg!
Grafisk metod för att konstruera en funktion
Den grafiska metoden för att konstruera en funktion är inte mindre bekväm. Vi ritar vår funktion, och en annan intresserad kan hitta vad y är lika med vid ett visst x och så vidare. Grafiska och analytiska metoder är bland de vanligaste.
Men här måste du komma ihåg vad vi pratade om i början - inte varje "squiggle" som ritas i koordinatsystemet är en funktion! Kommer du ihåg? För säkerhets skull kopierar jag här definitionen av vad en funktion är:
Som regel brukar folk nämna exakt de tre sätt att specificera en funktion som vi har diskuterat - analytiskt (med hjälp av en formel), tabellform och grafiskt, och glömmer helt bort att en funktion kan beskrivas verbalt. Så här? Ja, väldigt enkelt!
Verbal beskrivning av funktionen
Hur beskriver man en funktion verbalt? Låt oss ta vårt senaste exempel - . Denna funktion kan beskrivas som "varje verkligt värde på x motsvarar dess trippelvärde." Det är allt. Inget komplicerat. Du kommer naturligtvis att invända - "det finns så komplexa funktioner att det helt enkelt är omöjligt att specificera verbalt!" Ja, det finns sådana, men det finns funktioner som är lättare att beskriva verbalt än att definiera med en formel. Till exempel: "varje naturvärde av x motsvarar skillnaden mellan siffrorna som det består av, medan minuend antas vara den största siffran som finns i notationen av talet." Låt oss nu titta på hur vår verbala beskrivning av funktionen implementeras i praktiken:
Den största siffran i ett givet tal är respektive minuend, då:
Huvudtyper av funktioner
Låt oss nu gå vidare till den mest intressanta delen - låt oss titta på huvudtyperna av funktioner som du har arbetat/arbetar med och kommer att arbeta med i skol- och högskolematematiken, det vill säga låt oss lära känna dem, så att säga och ge dem en kort beskrivning. Läs mer om varje funktion i motsvarande avsnitt.
Linjär funktion
En funktion av formen där, är reella tal.
Grafen för denna funktion är en rak linje, så att konstruera en linjär funktion handlar om att hitta koordinaterna för två punkter.
Den räta linjens position på koordinatplanet beror på vinkelkoefficienten.

Omfattningen av en funktion (alias omfattningen av giltiga argumentvärden) är .
Värdeintervall - .
Kvadratisk funktion
Formens funktion, var
Funktionens graf är en parabel; när parabelns grenar är riktade nedåt, när grenarna är riktade uppåt.
Många egenskaper hos en kvadratisk funktion beror på diskriminantens värde. Diskriminanten beräknas med hjälp av formeln
Parabolens position på koordinatplanet i förhållande till värdet och koefficienten visas i figuren:

Domän
Värdeintervallet beror på extremumet för den givna funktionen (punktpunkten för parabeln) och koefficienten (riktningen för parabelns grenar)
Omvänd proportionalitet
Funktionen som ges av formeln, där
Talet kallas koefficienten för invers proportionalitet. Beroende på värdet är hyperbelns grenar i olika rutor:

Domän - .
Värdeintervall - .
SAMMANFATTNING OCH GRUNDFORMLER
1. En funktion är en regel enligt vilken varje element i en mängd är associerat med ett enda element i mängden.
- - detta är en formel som anger en funktion, det vill säga beroendet av en variabel av en annan;
- - variabelvärde eller argument;
- - beroende kvantitet - ändras när argumentet ändras, det vill säga enligt någon specifik formel som återspeglar beroendet av en kvantitet av en annan.
2. Giltiga argumentvärden, eller domänen för en funktion, är det som är förknippat med de möjligheter som funktionen är vettig i.
3. Funktionsområde- det är dessa värden som krävs, givet acceptabla värden.
4. Det finns fyra sätt att ställa in en funktion:
- analytisk (med formler);
- tabellform;
- grafisk
- verbal beskrivning.
5. Huvudtyper av funktioner:
- : , där, är reella tal;
- : , Var;
- : , Var.



