Плоскі та двогранні кути тригранного кута. Тригранний та багатогранний кути

2.4. Багатогранні кути

Відповідно до тематичного планування, на даний параграф відводиться одна година навчального часу (один урок).

1. Перевірка домашнього завдання (5 хв.)

2. Виконуємо етап роботи з інформацією (20 –25хв.)

p align="justify"> Технологічно етап орієнтований на переважне формування пізнавальних універсальних навчальних дій (уміння формулювати питання до тексту, самостійно формулювати відповіді з опорою на текст).

У цьому вся параграфі знаходить подальший розвиток поняття тригранного кута. З'являється багатогранний кут, у зв'язку з цим з'являється можливість уточнити поняття багатокутника.

У зв'язку із багатогранними кутами ще раз обговорюється проблема опуклості фігур. На прикладі багатогранних кутів ми додатково уточнюємо уявлення учнів про опуклі та неопуклі фігури (багатокутники, багатогранні кути, довільні фігури).

Для багатогранних кутів корисно сформулювати властивості їх плоских кутів, аналогічні до відповідних властивостей плоских кутів тригранного кута (без доказу):

1. Кожен плоский кут багатогранного кута менший за суму інших плоских кутів.

2. Сума всіх плоских кутів багатогранного кута менша за 360º.

3. Виконуємо етап розвитку умінь (15 –20 хв.)

Етап орієнтований на вироблення

пізнавальних УУД - формування умінь:

– щодо використання математичних знань для вирішення різних математичних завдань та оцінки отриманих результатів;

- З використанням доказової математичної мови;

– по роботі з інформацією, у тому числі з різними математичними текстами;

Регулятивних УУД - формування умінь ставити особисті цілі діяльності, планувати свою роботу, діяти за планом, оцінювати отримані результати;

комунікативних УУД – формування умінь разом із іншими дітьми групи шукати рішення завдання й оцінювати отримані результати.

Обговорюємо, що це етап роз'яснення всього незрозумілого та тренінгу. Встановлюємо цілі роботи на даному етапі, домагаючись при цьому від дітей особистого мети: роз'яснити для себевсе, що недостатньо добре зрозуміло, потренуватися у вирішенні завдань, які викликають труднощі.

Тут можна працювати з завданнями 34, 35 на стор. 29–30.

Пропонуємо також кілька додаткових завдань.

1) Багатогранний кут має nграней. Скільки у нього ребер?

Відповідь: nребер.

2) Чи можна виготовити модель чотиригранного кута із плоскими кутами: 1) 80°, 130°, 70°, 100°; 2) 45 °, 60 °, 120 °, 90 °; 3) 80 °, 80 °, 80 °, 80 °? Якщо модель вийшла, то якого кута: опуклого чи неопуклого?

Відповідь: 1) можна; 2) можна як опуклого, так і непуклого; 3) можна тільки опуклого.

3) Спираючись на відому властивість плоских кутів тригранного кута, доведіть, що кожен плоский кут чотиригранного кута менший за суму трьох інших його плоских кутів.

Вказівка: Через два протилежні ребра потрібно провести площину і розглянути тригранні кути. Доказ справедливий лише для опуклих кутів.

4) У чотиригранному куті всі плоскі кути рівні. Доведіть, що вони гострі.

Рішення: 1. Нехай α – градусний захід плоского кута.

2. Тоді 4α< 360° (по свойству суммы плоских углов выпуклого многогранного угла).

3. Отже, α< 90°, т. е. α – острый угол.

5) У опуклому багатогранному куті кожен із плоских кутів дорівнює а) 30°; б) 45 °; в) 80 °; г) 150 °. Скільки граней може мати такий багатогранний кут?

Відповідь: а) 3 ≤ n< 12; б) 3 ≤ n < 8; в) 3 ≤ n < 4,5; г) 3 ≤ n < 2,4 (такого многогранного угла не существует). При подсчетах нужно учитывать, что n- Число ціле.

6) У опуклому багатогранному куті всі плоскі кути рівні між собою. Багатогранний кут має: а) 6; б) 8; в) 10 граней. Чому можуть дорівнювати плоскі кути даного багатогранного кута?

Розмірковуємо так само, як і при розв'язанні задачі 5, n α < 360°, где n– кількість граней багатогранного кута, α – градусна міра плоского кута; 0 ≤ α< 360°/ n.

Відповідь: а) 0 ≤ α< 60°; б) 0 ≤ α< 45°; в) 0 ≤ α< 36°.

Після закінчення часу, відведеного до виконання завдань, результати роботи виносяться педагогом дошку і обговорюються учнями. Підбивається підсумок роботи, відбувається самооцінка, пов'язана з визначенням того, що ясно і виходить і того, що не ясно і не виходить.

4. Формулюємо домашнє завдання за різними рівнями складності – залежно від результатів роботи на попередньому етапі.

БАГАТОГРАНІ КУТИ

Багатогранний кут є просторовим аналогом багатокутника. Нагадаємо, що багатокутником на площині називається фігура, утворена простою замкненою ламаною та обмеженою нею внутрішньою областю. Вважатимемо аналогом точки на площині промінь у просторі та аналогом відрізка на площині плоский кут у просторі. Тоді аналогом простої замкнутої ламаної на площині є поверхня, утворена кінцевим набором плоских кутів.A 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 із загальною вершиноюS (рис. 1), у яких сусідні кути немає спільних точок, крім точок загального променя, а несусідні кути немає спільних точок, крім загальної вершини. Фігура, утворена зазначеною поверхнею та однією з двох частин простору, нею обмежених, називається багатогранним кутом. Загальна вершинаSназивається вершиноюбагатогранного кута. ПроменіSA 1 , …, SA nназиваються ребрамибагатогранного кута, а самі плоскі кутиA 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 – гранямибагатогранного кута. Багатогранний кут позначається літерамиSA 1 … A n, що вказують вершину та крапки на його ребрах. Залежно від числа граней багатогранні кути називаються тригранними, чотиригранними, п'ятигранними (рис. 2) тощо.

Багатогранний кут називається опуклим, якщо він є опуклою фігурою, тобто. разом з будь-якими двома своїми точками містить і з'єднує їхвідрізок. На малюнку 2 тригранний та чотиригранний кути опуклі, а п'ятигранний кут – ні.
Розглянемо деякі властивості трикутників та аналогічні їм властивості тригранних кутів.
Властивість 1(Нерівність трикутника). Кожна сторона трикутника менша за суму двох інших його сторін.
Аналогічним властивістю для тригранних кутів є така властивість.
Властивість 1Кожен плоский кут тригранного кута менший за суму двох інших його плоских кутів.
Доведення. Розглянемо тригранний кут SABC . Нехай найбільший із його плоских кутів є кут ASC. Тоді виконуються нерівності

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

Таким чином, залишається довести нерівність AСС< ASB+ BSC.
Відкладемо на межі ASCкут ASD, рівний ASB , і точку Bвиберемо так, щоб SB = SD(Рис. 3). Тоді трикутники ASBі ASDрівні (по обидва боки і кут між ними) і, отже, AB = AD. Скористаємося нерівністю трикутника AC< AB + BC . Віднімаючи з обох його частин AD = AB, отримаємо нерівність DC< BC. У трикутниках DSCі BSCодна сторона загальна ( SC), SD = SBі DC< BC. У цьому випадку проти більшої сторони лежить більший кут і, отже, DSC< BSC . Додаючи до обох частин цієї нерівності кут ASD , рівний ASB, отримаємо потрібну нерівність AСС< ASB+ BSC.

Наслідок 1.Сума плоских кутів тригранного кута менше 360° .
Доведення. Нехай SABC- Цей трикутний кут. Розглянемо тригранний кут із вершиною A, утворений гранями ABS, ACSта кутом BAC. З огляду на доведену властивість, має місце нерівність BАС< BAS+ CAS. Аналогічно для трикутних кутів з вершинами. Bі Змають місце нерівності: ABС< ABS+ CBS, ACB< ACS+ BCS. Складаючи ці нерівності та враховуючи, що сума кутів трикутника ABCдорівнює 180° , отримуємо 180 ° < BAS +CAS+ ABS + CBS + BCS+ ACS = 180 ° - ASB + 180° - BSC+ 180° - ASC. Отже, ASB + BSC + ASC< 360 ° .
Наслідок 2.Сума плоских кутів опуклого багатогранного кута менша за 360.
Доказ аналогічний попередньому.
Наслідок 3.Сума двогранних кутів тригранного кута більше 180° .
Доведення. Нехай SABC- Тригранний кут. Виберемо якусь точку Pусередині нього і опустимо з неї перпендикуляри PA 1 , PB 1 , PC 1 на межі (рис. 4).

Плоскі кути B 1 PC 1 , A 1 PC 1 , A 1 PB 1 доповнюють відповідні двогранні кути з ребрами SA, SB, SCдо 180° . Отже, сума цих двогранних кутів дорівнює 540° - ( B 1 PC 1 +A 1 PC 1 + A 1 PB 1 ). Враховуючи, що сума плоских трикутних кутів з вершиною Pкута менше 360° , Отримуємо, що сума двогранних кутів вихідного тригранного кута більше 180° .
Властивість 2.Бісектриси трикутника перетинаються в одній точці.
Властивість 2".Біссектральні площини двогранних кутів тригранного кута перетинаються однією прямою.
Доказ аналогічний плоскому випадку. А саме, нехай SABC- Тригранний кут. Біссектральна площина двогранного кута SAє ГМТ кута, рівновіддалених від його граней ASCі ASB. Аналогічно, біссектральна площина двогранного кута. SBє ГМТ кута, рівновіддалених від його граней BSAі BSC . Лінія їхнього перетину SOбуде рівновіддалена від усіх граней тригранного кута і, отже, через неї проходитиме біссектральна площина двогранного кута. SC .
Властивість 3.Серединні перпендикуляри до сторін трикутника перетинаються лише у точці.
Властивість 3".Площини, що проходять через бісектриси граней тригранного кута і перпендикулярні до цих граней, перетинаються по одній прямій.
Доказ аналогічний доведенню попередньої якості.
Властивість 4.Медіани трикутника перетинаються в одній точці.
Властивість 4".Площини, що проходять через ребра тригранного кута та бісектриси протилежних граней перетинаються по одній прямій.
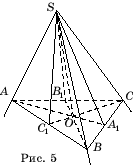
Доведення. Розглянемо тригранний кут SABC, SA = SB = SC(Рис. 5). Тоді бісектриси SA 1 , SB 1 , SC 1 кутів BSC, ASC, ASB є медіанами відповідних трикутників. Тому AA 1 , BB 1 , CC 1 – медіани трикутника ABC. Нехай O- Точка їх перетину. Пряма SOміститься у всіх трьох площинах, що розглядаються, і, отже, є лінією їх перетину.

Властивість 5.Висоти трикутника перетинаються в одній точці.
Властивість 5Площини, що проходять через ребра тригранного кута і перпендикулярні протилежним граням, перетинаються по одній прямій.
Доведення. Розглянемо тригранний кут із вершиною Sта ребрами a, b, c.Позначимо a 1 , b 1 , c 1 – лінії перетину граней з площинами, що проходять через відповідні ребра та перпендикулярні до цих граней (рис. 6). Зафіксуємо точку Cна ребрі cі опустимо з неї перпендикуляри CA 1 і CB 1 на прямі a 1 і b 1 . Позначимо Aі Bперетину прямих CA 1 і CB 1 з прямими aі b. Тоді SA 1 є проекцією AA 1 на межу BSC. Так як BCперпендикулярна SA 1 , то вона перпендикулярна і AA 1 . Аналогічно, ACперпендикулярна BB 1 . Таким чином, AA 1 та BB 1 є висотами трикутника ABC. Нехай O- Точка їх перетину. Площини, що проходять через прямі aі a 1 , bі b 1 перпендикулярні до площини ABCі, отже, лінія їхнього перетину SOперпендикулярна ABC. Значить, SOперпендикулярна AB. З іншого боку, COперпендикулярна AB. Тому площина, що проходить через ребро cі SOбуде перпендикулярна до протилежної грані.
Властивість 6 (теорема синусів). У трикутнику ABCзі сторонами a, b, cвідповідно, мають місце рівності a : sin A = b: sin B = c: sin C.
Властивість 6".Нехай a, b, g - Плоскі кути тригранного кута, a, b, c- Протилежні їм двогранні кути. Тоді sin a : sin a= sin b : sin b= sin g : sin c.
Доведення.Нехай SABC- Тригранний кут. Опустимо з точки Cперпендикуляр CC 1 на площину ASBта перпендикуляр CA 1 на ребро SA(Мал. 7). Тоді кут CA 1 C 1 буде лінійним кутом двогранного кута a. Тому CC 1 = CA 1 sin a = SC sin b sin a. Аналогічно показується, що CC 1 = CB 1 sin b = SC sin a sin b. Отже, має місце рівність sin b sin a = sin a sin bі, отже, рівність sin a: sin a= sin b : sin b. Аналогічним чином доводиться, що має місце рівність sin b : sin b= sin g : sin c.

Властивість 7.Якщо опуклий чотирикутник можна вписати коло, то суми протилежних сторін рівні.
Властивість 7".Якщо опуклий чотиригранний кут можна вписати сферу, то суми протилежних плоских кутів рівні.

Література
1. Адамар Ж. Елементарна геометрія. Частина ІІ. Стереометрія. - М.: Учпедгіз, 1938.
2. Перепілкін Д.І. Курс елементарної геометрії Частина ІІ. Геометрія у просторі. - М.-Л.: Гостехіздат, 1949.
3. Енциклопедія елементарної математики. Книга IV. Геометрія. - М.; 1963.
4. Смирнова І.М. У світі багатогранників. - М.: Просвітництво, 1995.

Двогранним кутом називається фігура, утворена двома напівплощинами із загальною прямою, що обмежує їх. Напівплощини називаються гранями, а пряма, що обмежує їх, - ребром двогранного кута.

На малюнку 142 зображено двогранний кут з ребром а та гранями а та (3.

Площина, перпендикулярна до ребра двогранного кута, перетинає його грані по двох напівпрямих. Кут, утворений цими напівпрямими, називається лінійним кутом двогранного кута. За міру двогранного кута приймається міра відповідного лінійного кута. Якщо через точку А ребра а двогранного кута провести площину у, перпендикулярну до цього ребра, то вона перетне площини а і (3 по напівпрямих (рис. 142); лінійний кут даного двогранного кута. Градусна міра цього лінійного кута є градусною мірою двогранного кута. двогранного кута залежить від вибору лінійного кута.

Тригранним кутом називається фігура, складена із трьох плоских кутів (рис. 143). Ці кути називаються гранями тригранного кута, які сторони - ребрами. Загальна вершина плоских кутів називається вершиною трикутного кута. Двогранні кути, що утворюються гранями та їх продовженнями, називаються двогранними кутами тригранного кута.

Аналогічно визначається поняття багатогранного кута як фігури, що складається з плоских кутів (рис. 144). Для багатогранного кута визначаються поняття граней, ребер та двогранних кутів так само, як і для тригранного кута.

Багатогранником називають тіло, поверхня якого складається з кінцевого числа плоских багатокутників (рис. 145).

Багатогранник називається опуклим, якщо він розташований з одного боку площини кожного багатокутника на його поверхні (рис. 145, а, б). Загальна частина такої площини та поверхні опуклого багатогранника називається гранню. Грані опуклого багатогранника – опуклі багатокутники. Сторони граней називаються ребрами багатогранника, а вершини – вершинами багатогранника.

Фігура, утворена трьома променями, що виходять з однієї точки і не лежать в одній площині, і трьома частинами площин, укладених між цими променями, називається тригранним кутом (рис. 352).

Точка О називається вершиною кута, промені а, b, з - його ребрами, частини площин. Грані суть плоскі кути, звані плоскими кутами даного тригранного кута. Кути між плоскими гранями називаються двогранними кутами цього тригранного кута.

Теорема 1. У тригранному куті кожен плоский кут менший за суму двох інших.

Доведення. Достатньо довести теорему для найбільшого із плоских кутів. Нехай максимальний плоский кут тригранного кута на рис. 353. Побудуємо в площині кут , рівний куту його сторона b пройде всередині кута кут найбільший із плоских кутів!).

Відкладемо на прямих с і b якісь рівні відрізки Проведемо через точки довільну площину, що перетинає промені а і b у точках N і М відповідно.

Трикутники рівні, як такі, що мають рівні кути, укладені між рівними сторонами. Покажемо, що кут з вершиною О в більший за кут з тією ж вершиною в . Справді, ці кути укладені між парами рівних сторін, третя сторона більше в трикутнику

Звідси видно, що сума двох плоских кутів більша за третій плоский кут що й вимагалося довести.

Теорема 2. Сума плоских кутів тригранного кута менша за чотири прямі.

Доведення. Візьмемо три точки А, В і С на ребрах тригранного кута і проведемо через них січну площину, як показано на рис. 354. Сума кутів трикутника ABC дорівнює Отже, сума шести кутів ОАС, ОАВ, ОСА, ОСВ, ОВС, ОВА більша, ніж за попередньою теоремою . Але сума кутів трьох трикутників ОАВ, ОВС, ОСА у гранях тригранного кута дорівнює . Таким чином, частку плоских кутів тригранного кута залишається менше чотирьох прямих: . Ця сума може бути як завгодно малою («трьохгранний шпиль») або як завгодно близькою до зменшувати висоту піраміди SABC на рис. 355, зберігаючи її основу, то сума плоских кутів при вершині S буде прагнути до

Сума двогранних кутів тригранного кута також має межі. Зрозуміло, кожен із двогранних кутів і тому сума їх менше . Для тієї ж піраміди на рис. 355 ця сума в міру зменшення висоти піраміди наближається до свого кордону Можна також показати, що ця сума завжди хоча може відрізнятися від скільки завгодно мало.

Таким чином, для плоских та двогранних кутів тригранного кута мають місце нерівності

Є суттєва схожість між геометрією трикутника на площині та геометрією тригранного кута. При цьому можна проводити аналогію між кутами трикутника і двогранними кутами тригранного кута, з одного боку, між сторонами трикутника і плоскими кутами тригранного кута - з іншого. Наприклад, при зазначеній заміні понять зберігають силу теореми про рівність трикутників. Наведемо відповідні формулювання паралельно:

Однак два тригранні кути, у яких рівні відповідні двогранні кути, рівні між собою. Тим часом два трикутники, кути яких відповідно рівні, подібні, але не обов'язково рівні. Для тригранних кутів, як й у трикутників, ставиться завдання розв'язання тригранного кута, т. е. завдання відшукання одних його елементів з іншим заданим. Наведемо приклад такого завдання.

Завдання. Дано плоскі кути тригранного кута. Знайти його двогранні кути.

Рішення. Відкладемо на ребрі а відрізок і проведемо нормальний переріз ABC двогранного кута. З прямокутного трикутника ОАВ знаходимо Також маємо

Для НД знаходимо по теоремі косінусів застосованої до трикутника ВАС (для стислості плоскі кути позначаємо просто ab, ас, bс, двогранні - а, b, с)

Тепер застосуємо теорему косінусів до трикутника ВОС:

Звідси знаходимо

та аналогічно

За цими формулами можна знайти двогранні кути, знаючи плоскі кути. Відзначимо ще без доказу чудове співвідношення

зване теоремою синусів.

Пояснення глибокої аналогії між геометрією тригранного кута та геометрією трикутника неважко отримати, якщо провести таку побудову. Помістимо у вершину тригранного кута О центр сфери одиничного радіусу (рис. 357).

Тоді ребра перетнуть поверхню сфери в трьох крапках А, В, С, грані кута висічуть на сфері дуги великих кіл АС, АВ, ВС. На сфері утворюється фігура ABC, яка називається сферичним трикутником. Дуги («сторони» трикутника) вимірюються плоскими кутами тригранного кута, кути при вершинах суть плоскі кути двогранних кутів. Тому розв'язання тригранних кутів є не що інше, як розв'язання сферичних трикутників, що є предметом сферичної тригонометрії. Співвідношення (243.1) і (243.2) відносяться до основних співвідношень сферичної тригонометрії. Сферична тригонометрія має важливе значення для астрономії. Таким чином, теорія тригранних кутів є теорією сферичних трикутників і тому багато в чому подібна до теорії трикутника на площині. Відмінність цих теорій полягає в тому, що: 1) у сферичного трикутника і кути та сторони вимірюються в кутовій мірі, тому, наприклад, у теоремі синусів фігурують не сторони, а синуси сторін АВ, АС, ВС;

№1 Дата05.09.14

Предмет Геометрія

Клас 11

Тема урока: Концепція багатогранного вугілля. Трикутний кут.

Цілі уроку:

запровадити поняття: "тригранні кути", "багатогранні кути", "багатогранник";

ознайомити учнів з елементами тригранного та багатогранного кутів, багатогранника, а також визначеннями опуклого багатогранного кута та властивостями плоских кутів багатогранного кута;

продовжити роботу з розвитку просторових уявлень та просторової уяви, а також логічного мислення учнів.

Тип уроку: вивчення нового матеріалу

ХІД УРОКУ

1. Організаційний момент.

Привітання учнів, перевірка готовності класу до уроку, організація уваги учнів, розкриття загальних цілей уроку та плану проведення.

2. Формування нових понять та способів дії.

Завдання: Забезпечити сприйняття, осмислення та запам'ятовування учнями матеріалу, що вивчається. Забезпечити засвоєння учнями методики відтворення вивченого матеріалу, сприяти філософському осмисленню понять, законів, правил, формул, що засвоюються. Встановити правильність та усвідомленість учнями вивченого матеріалу, виявити прогалини первинного осмислення, провести корекцію. Забезпечити співвідношення учнями свого суб'єктивного досвіду із ознаками наукового знання.

Нехай дані три променіа, b із с загальним початком крапкоюПро (Рис. 1.1). Ці три промені не обов'язково лежать в одній площині. На малюнку 1.2 променіb із лежать у площинір, а проміньа не лежить у цій площині.

Променіа, b із попарно задають три виділені дугами плоскі кути. (Рис. 1.3).

Розглянемо фігуру, що складається із трьох зазначених вище кутів та частини простору, обмеженої цими плоскими кутами. Цю просторову фігуру називаютьтригранним кутом (Рис. 2).

Променіа, b і з називаютьсяребрами тригранного кута, а кути: = AOC, = AOB,

= BOC , що обмежують тригранний кут, - йогогранями. Ці кути-грані утворюютьповерхню трикутного кута. КрапкаПро називаєтьсявершиною тригранного кута. Трикутний кут можна позначати так: OABC

Розглянувши уважно всі багатогранні кути, зображені малюнку 3, ми можемо зробити висновок, що з кожного з багатогранних кутів однакове число ребер і граней:

4 грані та одна вершина;

у п'ятигранного кута - 5 ребер, 5 граней та одна вершина;

• 
  у шестигранного кута - 6 ребер, 6 граней та одна вершина і т.д.

Багатогранні кути бувають опуклими і невипуклими.

Уявіть собі, що ми взяли чотири промені із загальним початком, як на малюнку 4. У цьому випадку ми отрималиневипуклий багатокутний кут.

Визначення 1. Багатогранний кут називається опуклим,якщо вінлежить по один бік від площини кожної його грані.

Іншими словами, опуклий багатогранний кут завжди можна покласти будь-якою його гранню на деяку площину. Ви бачите, що у випадку, зображеному на малюнку 4, так зробити не завжди вдається. Чотирьохгранний кут, зображений на малюнку 4, є неопуклим.

Зазначимо, що у нашому підручнику, якщо ми говоримо “багатогранний кут”, то маємо на увазі, що він опуклий. Якщо розглянутий багатокутний кут невипуклий, це буде сказано окремо.

Властивості плоских кутів багатогранного кута

Теорема 1.Кожен плоский кут тригранного кута менший за суму двох інших плоских кутів.

Теорема 2.Сума величин всіх плоских кутів опуклого багатогранного кута менша за 360°.

3. Застосування. Формування умінь та навичок.

Завдання: Забезпечити застосування учнями знань і способів дій, які їм необхідні СР, створити умови виявлення школярами індивідуальних способів застосування вивченого.

6.Етап інформації про домашнє завдання.

Завдання: Забезпечити розуміння учнями мети, змісту та способів виконання домашнього завдання.

§1(1.1, 1.2) стор. 4, № 9.

7.Підведення підсумків уроку.

Завдання: Дати якісну оцінку роботи класу та окремих учнів.

8. Етап рефлексії.

Завдання: Ініціювати рефлексію учнів самооцінку своєї діяльності. Забезпечити засвоєння учнями принципів саморегуляції та співробітництва.

Розмова з питань:

Що тобі на уроці було цікаво?

Що не зрозуміло?

На що звернути увагу вчителю на наступний урок?

Як ти оціниш свою роботу на уроці?