Табличні значення тригонометричних функцій. Cінус, косинус, тангенс і котангенс - все, що потрібно знати на ОГЕ та ЄДІ
Таблиця значень тригонометричних функцій
Примітка. У цій таблиці значень тригонометричних функцій використовується знак для позначення квадратного кореня. Для позначення дробу – символ "/".
Див. такожкорисні матеріали:
Для визначення значення тригонометричної функції, знайдіть його на перетині рядка із зазначенням тригонометричної функції. Наприклад, синус 30 градусів - шукаємо колонку із заголовком sin (синус) і знаходимо перетин цієї колонки таблиці з рядком "30 градусів", на їх перетині зчитуємо результат - одна друга. Аналогічно знаходимо косинус 60градусів, синус 60градусів (ще раз, у перетині колонки sin (синус) та рядки 60 градусів знаходимо значення sin 60 = √3/2) тощо. Так само знаходяться значення синусів, косінусів і тангенсів інших "популярних" кутів.
Синус пі, косинус пі, тангенс пі та інших кутів у радіанах
Наведена нижче таблиця косінусів, синусів та тангенсів також підходить для знаходження значення тригонометричних функцій, аргумент яких заданий у радіанах. Для цього скористайтеся другою колонкою значень кута. Завдяки цьому можна перевести значення популярних кутів із градусів у радіани. Наприклад, знайдемо кут 60 градусів у першому рядку і під ним прочитаємо його значення у радіанах. 60 градусів дорівнює π/3 радіан.
Число пі однозначно виражає залежність довжини кола від градусної міри кута. Таким чином, пі радіан дорівнюють 180 градусам.
Будь-яке число, виражене через пі (радіан), можна легко перевести в градусну міру, замінивши число пі (π) на 180.
Приклади:
1. Сінус пі.
sin π = sin 180 = 0
таким чином, синус пі - це те саме, що синус 180 градусів і він дорівнює нулю.
2. Косинус пі.
cos π = cos 180 = -1
таким чином, косинус пі - це те саме, що косинус 180 градусів і він дорівнює мінус одиниці.
3. Тангенс пі
tg π = tg 180 = 0
таким чином, тангенс пі - це те саме, що тангенс 180 градусів і він дорівнює нулю.
Таблиця значень синуса, косинуса, тангенса для кутів 0 - 360 градусів (часті значення)
|
значення кута α (градусів) |
значення кута α (через число пі) |
sin (синус) |
cos (Косінус) |
tg (тангенс) |
ctg (котангенс) |
sec (секанс) |
cosec (Косеканс) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
Якщо в таблиці значень тригонометричних функцій замість значення функції вказано прочерк (тангенс (tg) 90 градусів, котангенс (ctg) 180 градусів) означає, що при даному значенні градусної міри кута функція не має певного значення. Якщо прочерку немає - клітина порожня, значить ми ще не внесли потрібне значення. Ми цікавимося, за якими запитами до нас приходять користувачі і доповнюємо таблицю новими значеннями, незважаючи на те, що поточних даних про значення косинусів, синусів і тангенсів значень кутів, що найчастіше зустрічаються, цілком достатньо для вирішення більшості завдань.
Таблиця значень тригонометричних функцій sin, cos, tg для найпопулярніших кутів
0, 15, 30, 45, 60, 90...360 градусів
(Цифрові значення "як за таблицями Брадіса")
| значення кута α (градусів) | значення кута α у радіанах | sin (синус) | cos (косинус) | tg (тангенс) | ctg (котангенс) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
Припустимо, Ахіллес біжить у десять разів швидше, ніж черепаха, і знаходиться позаду неї на відстані тисячу кроків. За той час, за який Ахіллес пробіжить цю відстань, черепаха в той самий бік проповзе сто кроків. Коли Ахіллес пробіжить сто кроків, черепаха проповзе ще десять кроків, і таке інше. Процес продовжуватиметься до нескінченності, Ахіллес так ніколи і не наздожене черепаху.
Ця міркування стала логічним шоком для всіх наступних поколінь. Аристотель, Діоген, Кант, Гегель, Гільберт... Усі вони однак розглядали апорії Зенона. Шок виявився настільки сильним, що " ... дискусії продовжуються і в даний час, дійти спільної думки про сутність парадоксів науковому співтовариству поки що не вдалося... до дослідження питання залучалися математичний аналіз, теорія множин, нові фізичні та філософські підходи; жоден із них не став загальновизнаним вирішенням питання.[Вікіпедія, "Апорії Зенона"]. Всі розуміють, що їх дурять, але ніхто не розуміє, в чому полягає обман.
З погляду математики, Зенон у своїй апорії наочно продемонстрував перехід від величини до . Цей перехід передбачає застосування замість постійних. Наскільки розумію, математичний апарат застосування змінних одиниць виміру або ще розроблено, або його застосовували до апорії Зенона. Застосування нашої звичайної логіки приводить нас у пастку. Ми, за інерцією мислення, застосовуємо постійні одиниці виміру часу до оберненої величини. З фізичної точки зору це виглядає як уповільнення часу до його повної зупинки в момент, коли Ахілес порівняється з черепахою. Якщо час зупиняється, Ахілес вже не може перегнати черепаху.
Якщо перевернути звичну нам логіку, все стає на свої місця. Ахілес біжить з постійною швидкістю. Кожен наступний відрізок його шляху вдесятеро коротший за попередній. Відповідно, і час, що витрачається на його подолання, у десять разів менший за попередній. Якщо застосовувати поняття "нескінченність" у цій ситуації, то правильно буде говорити "Ахіллес нескінченно швидко наздожене черепаху".
Як уникнути цієї логічної пастки? Залишатися в постійних одиницях виміру часу і переходити до зворотним величинам. Мовою Зенона це виглядає так:
За той час, за який Ахіллес пробіжить тисячу кроків, черепаха в той самий бік проповзе сто кроків. За наступний інтервал часу, що дорівнює першому, Ахіллес пробіжить ще тисячу кроків, а черепаха проповзе сто кроків. Тепер Ахіллес на вісімсот кроків випереджає черепаху.
Цей підхід адекватно визначає реальність без жодних логічних парадоксів. Але це не повне вирішення проблеми. На Зеноновську апорію "Ахіллес і черепаха" дуже схоже твердження Ейнштейна про непереборність швидкості світла. Цю проблему нам ще належить вивчити, переосмислити та вирішити. І рішення потрібно шукати не в нескінченно великих числах, а в одиницях виміру.
Інша цікава апорія Зенона оповідає про стрілу, що летить.
Летяча стріла нерухома, тому що в кожний момент часу вона спочиває, а оскільки вона спочиває в кожний момент часу, вона завжди спочиває.
У цій апорії логічний парадокс долається дуже просто - досить уточнити, що в кожний момент часу стріла, що летить, спочиває в різних точках простору, що, власне, і є рухом. Тут слід зазначити інший момент. За однією фотографією автомобіля на дорозі неможливо визначити ані факт його руху, ані відстань до нього. Для визначення факту руху автомобіля потрібні дві фотографії, зроблені з однієї точки в різні моменти часу, але не можна визначити відстань. Для визначення відстані до автомобіля потрібні дві фотографії, зроблені з різних точок простору в один момент часу, але не можна визначити факт руху (природно, ще потрібні додаткові дані для розрахунків, тригонометрія вам на допомогу). На що я хочу звернути особливу увагу, то це на те, що дві точки в часі та дві точки в просторі – це різні речі, які не варто плутати, адже вони надають різні можливості для дослідження.
середа, 4 липня 2018 р.
Дуже добре відмінності між безліччю та мультимножиною описані у Вікіпедії. Дивимося.
Як бачите, "у множині не може бути двох ідентичних елементів", але якщо ідентичні елементи у множині є, така множина називається "мультимножина". Подібну логіку абсурду розумним істотам не зрозуміти ніколи. Це рівень папуг, що говорять, і дресованих мавп, у яких розум відсутній від слова "зовсім". Математики виступають у ролі звичайних дресирувальників, проповідуючи нам свої абсурдні ідеї.
Колись інженери, які збудували міст, під час випробувань мосту перебували у човні під мостом. Якщо міст обрушувався, бездарний інженер гинув під уламками свого творіння. Якщо міст витримував навантаження, талановитий інженер будував інші мости.
Як би математики не ховалися за фразою "чур, я в будиночку", точніше "математика вивчає абстрактні поняття", є одна пуповина, яка нерозривно пов'язує їх із реальністю. Цією пуповиною є гроші. Застосуємо математичну теорію множин до самих математиків.
Ми дуже добре вчили математику і зараз сидимо у касі, видаємо зарплатню. Ось приходить до нас математик по свої гроші. Відраховуємо йому всю суму та розкладаємо у себе на столі на різні стопки, в які складаємо купюри однієї гідності. Потім беремо з кожної стопки по одній купюрі та вручаємо математику його "математичну безліч зарплати". Пояснюємо математику, що решта купюр він отримає тільки тоді, коли доведе, що безліч без однакових елементів не дорівнює безлічі з однаковими елементами. Ось тут почнеться найцікавіше.
Насамперед спрацює логіка депутатів: "до інших це застосовувати можна, до мене - низьзя!". Далі почнуться запевнення нас у тому, що на купюрах однакової гідності є різні номери купюр, а отже, їх не можна вважати однаковими елементами. Добре, відраховуємо зарплату монетами – на монетах немає номерів. Тут математик почне судомно згадувати фізику: на різних монетах є різна кількість бруду, кристалічна структура та розташування атомів у кожної монети унікально.
А тепер у мене найцікавіше питання: де проходить та грань, за якою елементи мультимножини перетворюються на елементи множини і навпаки? Такої межі не існує – все вирішують шамани, наука тут і близько не валялася.
Ось дивіться. Ми відбираємо футбольні стадіони із однаковою площею поля. Площа полів однакова – значить у нас вийшло мультимножина. Але якщо розглядати назви цих стадіонів - у нас виходить безліч, адже назви різні. Як бачите, той самий набір елементів одночасно є і безліччю, і мультимножиною. Як правильно? А ось тут математик-шаман-шуллер дістає з рукава козирний туз і починає нам розповідати або про множину, або про мультимножину. У будь-якому разі він переконає нас у своїй правоті.
Щоб зрозуміти, як сучасні шамани оперують теорією множин, прив'язуючи її до реальності, достатньо відповісти на одне питання: чим елементи однієї множини відрізняються від елементів іншої множини? Я вам покажу, без усяких "мислиме як єдине ціле" чи "не мислиме як єдине ціле".
неділя, 18 березня 2018 р.
Сума цифр числа - це танець шаманів з бубном, який до математики жодного стосунку не має. Так, на уроках математики нас вчать знаходити суму цифр числа та користуватися нею, але на те вони й шамани, щоб навчати нащадків своїм навичкам та премудростям, інакше шамани просто вимруть.
Вам потрібні докази? Відкрийте Вікіпедію та спробуйте знайти сторінку "Сума цифр числа". Її немає. Немає в математиці формули, якою можна знайти суму цифр будь-якого числа. Адже цифри - це графічні символи, з яких записуємо числа і мовою математики завдання звучить так: "Знайти суму графічних символів, що зображують будь-яке число". Математики це завдання вирішити що неспроможні, тоді як шамани - елементарно.
Давайте розберемося, що як ми робимо у тому, щоб знайти суму цифр заданого числа. Тож нехай у нас є число 12345. Що потрібно зробити для того, щоб знайти суму цифр цього числа? Розглянемо всі кроки по порядку.
1. Записуємо число на папірці. Що ми зробили? Ми перетворили число на графічний символ числа. Це не математична дія.
2. Розрізаємо одну отриману картинку на кілька картинок, що містять окремі цифри. Розрізання картинки - це математична дія.
3. Перетворюємо окремі графічні символи на числа. Це не математична дія.
4. Складаємо отримані числа. Це вже математика.
Сума цифр числа 12345 дорівнює 15. Ось такі ось "курси крою та шиття" від шаманів застосовують математики. Але це ще не все.
З погляду математики немає значення, у якій системі числення ми записуємо число. Так от, у різних системах числення сума цифр одного і того ж числа буде різною. У математиці система числення вказується як нижнього індексу праворуч від числа. З великим числом 12345 я не хочу голову морочити, розглянемо число 26 статті про . Запишемо це число у двійковій, вісімковій, десятковій та шістнадцятковій системах числення. Ми не розглядатимемо кожен крок під мікроскопом, це ми вже зробили. Подивимося результат.
Як бачите, у різних системах числення сума цифр одного й того ж числа виходить різною. Подібний результат до математики жодного стосунку не має. Це все одно, що при визначенні площі прямокутника в метрах і сантиметрах ви отримували б різні результати.
Нуль у всіх системах числення виглядає однаково і суми цифр немає. Це ще один аргумент на користь того, що . Питання математикам: як у математиці позначається те, що є числом? Що для математиків нічого, крім чисел, не існує? Для шаманів я можу таке припустити, але для вчених – ні. Реальність складається не лише з чисел.
Отриманий результат слід як доказ те, що системи числення є одиницями виміру чисел. Адже ми не можемо порівнювати числа з різними одиницями виміру. Якщо одні й самі дії з різними одиницями виміру однієї й тієї величини призводять до різних результатів після їх порівняння, це має нічого спільного з математикою.
Що таке справжня математика? Це коли результат математичної дії не залежить від величини числа, що застосовується одиниці виміру і від того, хто цю дію виконує.
Ой! А це хіба не жіночий туалет?
- Дівчино! Це лабораторія з вивчення індефільної святості душ під час вознесіння на небеса! Німб зверху і стрілка вгору. Який ще туалет?
Жіночий... Німб зверху та стрілочка вниз – це чоловічий.
Якщо у вас перед очима кілька разів на день мелькає ось такий витвір дизайнерського мистецтва,
Тоді не дивно, що у своєму автомобілі ви раптом виявляєте дивний значок:
Особисто я роблю над собою зусилля, щоб в людині, яка кавала (одна картинка), побачити мінус чотири градуси (композиція з декількох картинок: знак мінус, цифра чотири, позначення градусів). І я не вважаю цю дівчину дурницею, яка не знає фізики. Просто вона має дугою стереотип сприйняття графічних образів. І математики нас цього постійно навчають. Ось приклад.
1А - це не "мінус чотири градуси" або "один а". Це "какая людина" або число "двадцять шість" у шістнадцятковій системі числення. Ті люди, які постійно працюють у цій системі числення, автоматично сприймають цифру та букву як один графічний символ.
Увага!
До цієї теми є додаткові
матеріали у розділі 555.
Для тих, хто сильно "не дуже..."
І для тих, хто "дуже навіть...")
Насамперед нагадаю простий, але дуже корисний висновок з уроку "Що таке синус та косинус? Що таке тангенс та котангенс?"
Ось цей висновок:
Синус, косинус, тангенс та котангенс міцно пов'язані зі своїми кутами. Знаємо одне – значить, знаємо й інше.
Іншими словами, кожен кут має свій незмінний синус і косинус. І майже у кожного – свій тангенс та котангенс. Чому майже?Про це нижче.
Це знання чудово допомагає в навчанні! Існує маса завдань, де потрібно перейти від синусів до кутів і навпаки. Для цього існує таблиці синусів.Аналогічно, для завдань із косинусом - таблиці косінусів.І, як ви вже здогадалися, існує таблиця тангенсіві таблиця котангенсів.)
Таблиці бувають різні. Довгі, де можна подивитися, до чого дорівнює, скажімо, sin37°6'. Розкриваємо таблиці Брадіса, шукаємо кут тридцять сім градусів шість хвилин і бачимо значення 0,6032. Зрозуміло, запам'ятовувати це число (і тисячі інших табличних значень) зовсім не потрібно.
По суті, в наш час довгі таблиці косінусів синусів тангенсів котангенсів не надто й потрібні. Один гарний калькулятор замінює їх повністю. Але знати існування таких таблиць не заважає. Для загальної ерудиції.)
І навіщо тоді цей урок? - Запитайте ви.
А ось навіщо. Серед нескінченної кількості кутів є особливі,про які ви повинні знати Усе. На цих кутах побудовано всю шкільну геометрію і тригонометрію. Це, свого роду, "таблиця множення" тригонометрії. Якщо ви не знаєте, чому дорівнює, наприклад sin50°, ніхто вас не засудить.) Але якщо ви не знаєте, чому дорівнює sin30°, будьте готові отримати заслужену двійку...
Таких особливихкутів теж пристойно набирається. Шкільні підручники зазвичай люб'язно пропонують до запам'ятовування таблицю синусів та таблицю косинусівдля сімнадцяти кутів. Ну і, зрозуміло, таблицю тангенсів та таблицю котангенсівдля тих самих сімнадцяти кутів... Тобто. пропонується запам'ятати 68 значень. Які, між іншим, дуже схожі між собою, раз у раз повторюються і змінюють знаки. Для людини без ідеальної зорової пам'яті - та ще завдання ...)
Ми підемо іншим шляхом. Замінимо механічне запам'ятовування на логіку та кмітливість. Тоді нам доведеться зазубрити 3 (три!) значення для таблиці синусів та таблиці косінусів. І 3 (три!) Значення для таблиці тангенсів та таблиці котангенсів. І все. Шість значень запам'ятати легше, ніж 68, мені здається...)
Всі інші необхідні значення ми отримуватимемо з цих шести за допомогою потужної законної шпаргалки - Тригонометричного кола. Якщо ви не вивчали цю тему, сходіть за посиланням, не лінуйтеся. Це коло не тільки для цього уроку потрібне. Він незамінний для всієї тригонометрії відразу. Чи не користуватися таким інструментом просто гріх! Не хочете? Справа ваша. Завчайте таблиці синусів. Таблицю косінусів. Таблиця тангенсів. Таблиця котангенсів.Усі 68 значень для різноманітних кутів.)
Тож почнемо. Для початку розіб'ємо всі ці спеціальні кути на три групи.
Перша група кутів.
Розглянемо першу групу кутів із сімнадцяти особливих. Це 5 кутів: 0 °, 90 °, 180 °, 270 °, 360 °.
Ось так виглядає таблиця синусів косинусів тангенсів котангенсів для цих кутів:
Кут х
|
0 |
90 |
180 |
270 |
360 |
Кут х
|
0 |
||||
sin x |
0 |
1 |
0 |
-1 |
0 |
cos x |
1 |
0 |
-1 |
0 |
1 |
tg x |
0 |
не сущ. |
0 |
не сущ. |
0 |
ctg x |
не сущ. |
0 |
не сущ. |
0 |
не сущ. |
Охочі запам'ятати - запам'ятовуйте. Але одразу скажу, що всі ці одиниці та нулики дуже плутаються в голові. Набагато сильніше, ніж хочеться.) Тому включаємо логіку та тригонометричне коло.
Малюємо коло і відзначаємо на ньому ці самі кути: 0 °, 90 °, 180 °, 270 °, 360 °. Я ці кути відзначив червоними крапками:

Відразу видно, у чому особливість цих кутів. Так! Це кути, які потрапляють точно на осі координат!Власне, тому і плутається народ... Але ми плутатися не будемо. Розберемося, як шукати тригонометричні функції цих кутів без особливого запам'ятовування.
До речі, положення кута 0 градусів повністю збігаєтьсяз положенням кута 360 градусів. Це означає, що синуси, косинуси, тангенси цих кутів абсолютно однакові. Кут 360 градусів я відзначив, щоб замкнути коло.
Припустимо, у складній стресовій обстановці ЄДІ ви якось засумнівалися... Чому дорівнює синус 0 градусів? Наче нуль... А раптом одиниця?! Механічне запам'ятовування така штука. У суворих умовах сумніви є починають...)
Спокій, тільки спокій!) Я підкажу вам практичний прийом, який видасть стовідсотково правильну відповідь і повністю прибере всі сумніви.
Як приклад розберемося, як чітко та надійно визначити, скажімо, синус 0 градусів. А заразом, і косинус 0. Саме в цих значеннях, як не дивно, часто люди плутаються.
Для цього на колі намалюємо довільнийкут х. У першій чверті щоб недалеко від 0 градусів було. Відзначимо на осях синус та косинус цього кута х,все чин-чинарем. Ось так:
А тепер – увага! Зменшимо кут х, наблизимо рухомий бік до осі ОХ. Наведіть курсор на зображення (або торкніться зображення на планшеті) і все побачите.
Тепер включаємо елементарну логіку!Дивимося та розмірковуємо: як поводиться sinx при зменшенні кута х? При наближенні кута до нуля?Він зменшується! А cosx – збільшується!Залишається збагнути, що станеться з синусом, коли кут зникне зовсім? Коли рухома сторона кута (точка А) уляжеться на вісь ОХ і кут стане рівним нулю? Очевидно, і синус кута піде в нуль. А косинус збільшиться до... до... Чому дорівнює довжина рухомого боку кута (радіус тригонометричного кола)? Одиниці!
Ось і відповідь. Синус 0 градусів дорівнює 0. Косинус 0 градусів дорівнює 1. Цілком залізно і без жодних сумнівів!) Просто тому, що інакше бути не може.
Абсолютно аналогічно можна дізнатися (або уточнити) синус 270 градусів, наприклад. Або косинус 180. Намалювати коло, довільнийкут в чверті поряд з віссю координат, що цікавить нас, подумки спонукати бік кута і вловити, чим стане синус і косинус, коли сторона кута вляжеться на вісь. От і все.
Як бачите, для цієї групи кутів нічого заучувати не треба. Не потрібна тут таблиця синусів...Та й таблиця косінусів- теж.) До речі, після кількох застосувань тригонометричного кола всі ці значення запам'ятаються самі собою. А якщо забудуться – намалював за 5 секунд коло та уточнив. Куди простіше, ніж дзвонити другові з туалету з ризиком для атестату, правда?)
Що стосується тангенсу і котангенсу - все те саме. Малюємо на колі лінію тангенсу (котангенсу) – і все відразу видно. Де вони дорівнюють нулю, а де - не існують. Що, не знаєте про лінії тангенсу та котангенсу? Це сумно, але можна виправити.) Відвідали Розділ 555 Тангенс і котангенс на тригонометричному колі - і немає проблем!
Якщо ви зрозуміли, як чітко визначити синус, косинус, тангенс та котангенс для цих п'яти кутів – я вас вітаю! Про всяк випадок повідомляю, що ви тепер можете визначати функції будь-яких кутів, що потрапляють на осі.А це і 450 °, і 540 °, і 1800 °, і ще нескінченна кількість ...) Відрахував (правильно!) Кут на колі - і немає проблем з функціями.
Але саме з відрахуванням кутів і трапляються проблеми та помилки... Як їх уникнути, написано в уроці: Як намалювати (відрахувати) будь-який кут на тригонометричному колі в градусах. Елементарно, але дуже допомагає у боротьбі з помилками.)
А ось урок: Як намалювати (відрахувати) будь-який кут на тригонометричному колі в радіанах – крутіше буде. У сенсі можливостей. Скажімо, визначити, на яку з чотирьох півосей потрапляє кут
ви зможете за кілька секунд. Я не шуткую! Саме за кілька секунд. Ну, звичайно, не тільки 345 "пі"...) І 121, і 16, і -1345. Будь-який цілий коефіцієнт підходить для миттєвої відповіді.
А якщо кут
Подумаєш! Вірна відповідь виходить секунд за 10. Для будь-якого дробового значення радіанів із двійкою у знаменнику.
Власне, цим і добре тригонометричне коло. Тим, що вміння працювати з деякимикутами він автоматично розширює на нескінченна безлічкутів.
Отже, з п'ятьма кутами із сімнадцяти – розібралися.
Друга група кутів.
Наступна група кутів - це кути 30 °, 45 ° і 60 °. Чому саме ці, а не, наприклад, 20, 50 та 80? Так якось склалося так... Історично.) Далі буде видно, чим гарні ці кути.
Таблиця синусів косинусів тангенсів котангенсів для цих кутів виглядає так:
Кут х
|
0 |
30 |
45 |
60 |
90 |
Кут х
|
0 |
||||
sin x |
0 |
1 |
|||
cos x |
1 |
0 |
|||
tg x |
0 |
1 |
не сущ. |
||
ctg x |
не сущ. |
1 |
0 |
Я залишив значення для 0° та 90° з попередньої таблиці для завершеності картини.) Щоб було видно, що ці кути лежать у першій чверті та зростають. Від 0 до 90. Це стане нам у нагоді далі.
Значення таблиці для кутів 30°, 45° та 60° слід запам'ятати. Зазубрити, якщо хочете. Але і тут є можливість полегшити собі життя. Зверніть увагу на значення таблиці синусівцих кутів. І порівняйте зі значеннями таблиці косінусів...
Так! Вони одні й ті ж!Тільки розташовані у зворотному порядку. Кути зростають (0, 30, 45, 60, 90) - та значення синуса зростаютьвід 0 до 1. Ви можете переконатися з калькулятором. А значення косинуса - спадаютьвід 1 до нуля. Причому самі значення одні й ті ж.Для кутів 20, 50, 80 так би не вийшло...
Звідси корисний висновок. Достатньо вивчити тризначення для кутів 30, 45, 60 градусів. І пам'ятати, що у синуса вони зростають, а у косинуса – зменшуються. Назустріч синусу.) На половині шляху (45 °) вони зустрічаються, тобто синус 45 градусів дорівнює косінус 45 градусів. А далі знову розходяться... Три значення можна вивчити, правда?
З тангенсами - котангенсами картина виключно та сама. Один в один. Лише значення інші. Ці значення (ще три!) теж треба вивчити.
Ну ось, практично все запам'ятовування закінчилося. Ви зрозуміли (сподіваюся), як визначати значення для п'яти кутів на осі і вивчили значення для кутів 30, 45, 60 градусів. Усього 8.
Залишилося розібратися з останньою групою із 9 кутів.
Ось ці кути:
120 °; 135 °; 150 °; 210 °; 225 °; 240 °; 300 °; 315 °; 330 °. Для цих кутів треба залізно знати таблицю синусів, таблицю косінусів тощо.
Кошмар, правда?)
А якщо додати сюди кути, типу: 405 °, 600 °, або 3000 ° і багато-багато такого ж красивого?)
Чи кути у радіанах? Наприклад, про кути:

і багато інших, ви повинні знати Усе.
Найцікавіше, що знати це Усе - неможливо у принципі.Якщо використати механічну пам'ять.
І дуже легко, фактично елементарно – якщо використовувати тригонометричне коло. Якщо ви освоїте практичну роботу з тригонометричним колом, всі ці жахливі кути в градусах будуть легко і елегантно зводитися до старих добрих:
До речі, у мене є ще кілька цікавих сайтів для Вас.)
Можна потренуватися у вирішенні прикладів та дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося – з інтересом!)
можна познайомитися з функціями та похідними.
У статті ми повністю розберемося, як виглядає таблиця тригонометричних значень, синуса, косинуса, тангенсу та котангенсу. Розглянемо основне значення тригонометричних функцій, від кута 0,30,45,60,90,...,360 градусів. І подивимося як користуватись даними таблицями у обчисленні значення тригонометричних функцій.
Першою розглянемо таблицю косинуса, синуса, тангенсу та котангенсувід кута в 0, 30, 45, 60, 90, .. градусів. Визначення даних величин дають визначити значення функцій кутів 0 і 90 градусів:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, котангенс від 00 буде невизначеним
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс від 90 0 буде невизначеним
Якщо взяти прямокутні трикутники кути яких від 30 до 90 градусів. Отримаємо:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Зобразимо всі отримані значення як тригонометричної таблиці:
Таблиця синусів, косінусів, тангенсів та котангенсів!
Якщо використовувати формулу приведення, то наша таблиця збільшиться, додадуться значення для кутів до 360 градусів. Виглядатиме вона як:

Також виходячи з властивостей періодичності таблицю можна збільшити, якщо замінимо кути на 0 0 +360 0 *z .... 330 0 +360 0 *z, в якому z є цілим числом. У цій таблиці можна визначити значення всіх кутів, відповідними точками в єдиному колі.
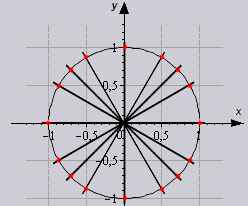
Розберемо наочно використовувати таблицю у рішенні.
Все дуже просто. Оскільки необхідне значення лежить у точці перетину необхідних нам осередків. Наприклад візьмемо cos кута 60 градусів, у таблиці це буде виглядати як:

У підсумковій таблиці основних значень тригонометричних функцій діємо так само. Але в цій таблиці можна дізнатися скільки складе тангенс від кута в 1020 градусів, він = -√3 Перевіримо 1020 0 = 300 0 +360 0 *2. Знайдемо за таблицею.

Таблиця Брадіса. Для синуса, косинуса, тангенсу та котангенсу.
Таблиці Брадіса поділені на кілька частин, складаються з таблиць косинуса та синуса, тангенсу та котангенсу - яка поділена на дві частини (tg кута до 90 градусів і ctg малих кутів).
Синус та косинус


tg кута з 00 закінчуючи 760, ctg кута з 140 закінчуючи 900.
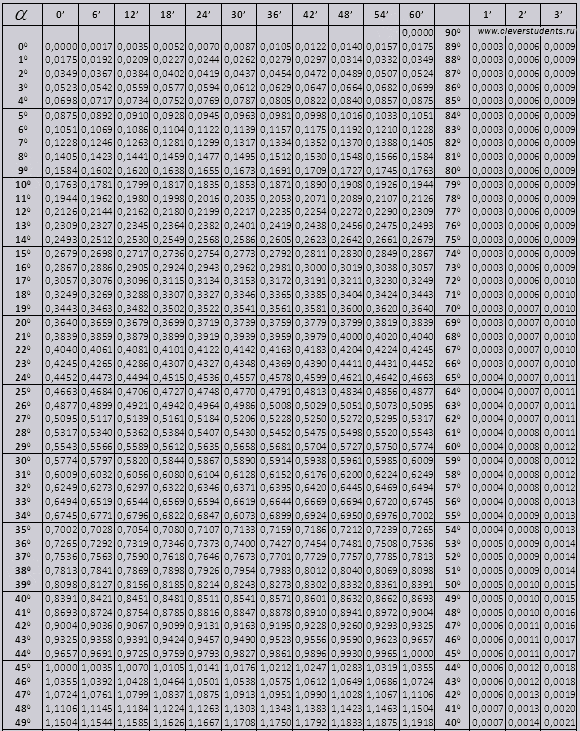

tg до 900 та ctg малих кутів.


Розберемося як користуватися таблицями Брадіса у вирішенні завдань.
Знайдемо позначення sin (позначення в стовпці з лівого краю) 42 хвилини (позначення знаходиться на верхньому рядку). Шляхом перетину шукаємо позначення, воно = 0,3040.
Величини хвилин вказані з проміжком у шість хвилин, як бути, якщо потрібне нам значення потрапить саме в цей проміжок. Візьмемо 44 хвилини, а в таблиці є тільки 42. Беремо за основу 42 і скористаємося додатковими стовпцями в правій стороні, беремо 2 поправку і додаємо до 0,3040 + 0,0006, отримуємо 0,3046.
При sin 47 хв беремо за основу 48 хв і віднімаємо від неї 1 поправку, тобто 0,3057 - 0,0003 = 0,3054
При обчисленні cos працюємо аналогічно sin тільки за основу беремо нижній рядок таблиці. Наприклад cos 20 0 = 0.9397
Значення tg кута до 90 0 і cot малого кута, вірні та поправок у них немає. Наприклад, визначити tg 78 0 37хв = 4,967 
а ctg 20 0 13хв = 25,83 
Ну, ось ми і розглянули основні тригонометричні таблиці. Сподіваємося, ця інформація була для вас вкрай корисною. Свої питання щодо таблиць, якщо вони з'явилися, обов'язково пишіть у коментарях!
Стінові відбійники - відбійна дошка для захисту стін. Перейдіть за посиланням настінні безкаркасні відбійники (http://www.spi-polymer.ru/otboyniki/) і дізнайтесь докладніше.
Тригонометрія, як наука, зародилася на Стародавньому Сході. Перші тригонометричні співвідношення були виведені астрономами для створення точного календаря та орієнтування за зірками. Дані обчислення належали до сферичної тригонометрії, тоді як у шкільному курсі вивчають співвідношення сторін та кута плоского трикутника.
Тригонометрія – це розділ математики, що займається властивостями тригонометричних функцій та залежністю між сторонами та кутами трикутників.
У період розквіту культури та науки I тисячоліття нашої ери знання поширилися з Стародавнього Сходу до Греції. Але основні відкриття тригонометрії – заслуга чоловіків арабського халіфату. Зокрема, туркменський учений аль-Маразві ввів такі функції, як тангенс та котангенс, склав перші таблиці значень для синусів, тангенсів та котангенсів. Поняття синуса та косинуса введено індійськими вченими. Тригонометрії присвячено чимало уваги у працях таких великих діячів давнини, як Евкліда, Архімеда та Ератосфена.
Основні величини тригонометрії
Основні тригонометричні функції числового аргументу – це синус, косинус, тангенс та котангенс. Кожна з них має свій графік: синусоїда, косінусоїда, тангенсоїда та котангенсоїда.
У основі формул до розрахунку значень зазначених величин лежить теорема Піфагора. Школярам вона більше відома у формулюванні: «Піфагорові штани, на всі боки рівні», оскільки доказ наводиться на прикладі рівнобедреного прямокутного трикутника.
Синус, косинус та інші залежності встановлюють зв'язок між гострими кутами та сторонами будь-якого прямокутного трикутника. Наведемо формули для розрахунку цих величин для кута A і простежимо взаємозв'язки тригонометричних функцій:

Як видно, tg та ctg є зворотними функціями. Якщо уявити катет a як добуток sin A та гіпотенузи с, а катет b у вигляді cos A * c, то отримаємо такі формули для тангенсу та котангенсу:

Тригонометричне коло
Графічно співвідношення згаданих величин можна так:

Коло, в даному випадку, являє собою всі можливі значення кута - від 0° до 360°. Як видно з малюнка, кожна функція набуває негативного або позитивного значення в залежності від величини кута. Наприклад, sin α буде зі знаком «+», якщо α належить І і ІІ чверті кола, тобто знаходиться у проміжку від 0° до 180°. При від 180° до 360° (III і IV чверті) sin α може бути тільки негативним значенням.
Спробуємо побудувати тригонометричні таблиці для конкретних кутів та дізнатися значення величин.

Значення α рівні 30°, 45°, 60°, 90°, 180° тощо – називають окремими випадками. Значення тригонометричних функцій їм прораховані і представлені у вигляді спеціальних таблиць.

Ці кути обрані зовсім не випадково. Позначення π у таблицях стоїть для радіан. Радий - це кут, при якому довжина дуги кола відповідає її радіусу. Дана величина була введена для того, щоб встановити універсальну залежність, при розрахунках у радіанах не має значення дійсна довжина радіуса см.

Кути в таблицях для тригонометричних функцій відповідають значенням радіан:

Отже, не важко здогадатися, що 2π - це повне коло або 360 °.
Властивості тригонометричних функцій: синус та косинус
Для того, щоб розглянути та порівняти основні властивості синуса та косинуса, тангенсу та котангенсу, необхідно накреслити їх функції. Зробити це можна у вигляді кривої, розташованої у двовимірній системі координат.
Розглянь порівняльну таблицю властивостей для синусоїди та косінусоїди:

| Синусоїда | Косинусоїда |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, де k ϵ Z | cos x = 0 при x = π/2 + πk, де k ϵ Z |
| sin x = 1, за x = π/2 + 2πk, де k ϵ Z | cos x = 1 при x = 2πk, де k ϵ Z |
| sin x = - 1 при x = 3π/2 + 2πk, де k ϵ Z | cos x = - 1 при x = π + 2πk, де k ϵ Z |
| sin (-x) = - sin x, тобто функція непарна | cos (-x) = cos x, тобто функція парна |
| функція періодична, найменший період - 2π | |
| sin x › 0, при x належить I і II чвертям або від 0° до 180° (2πk, π + 2πk) | cos x › 0, при x належить I і IV чвертям або від 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x належить III і IV чвертям або від 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x належить II і III чвертям або від 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| зростає на проміжку [- π/2 + 2πk, π/2 + 2πk] | зростає на проміжку [-π + 2πk, 2πk] |
| зменшується на проміжках [ π/2 + 2πk, 3π/2 + 2πk] | зменшується на проміжках |
| похідна (sin x)’ = cos x | похідна (cos x)' = - sin x |
Визначити чи є функція парною чи ні дуже просто. Достатньо уявити тригонометричний круг зі знаками тригонометричних величин і подумки «скласти» графік щодо осі OX. Якщо знаки збігаються, функція парна, інакше непарна.

Введення радіан та перерахування основних властивостей синусоїди та косінусоїди дозволяють навести наступну закономірність:

Переконатись у вірності формули дуже просто. Наприклад, для x = π/2 синус дорівнює 1, як і косинус x = 0. Перевірку можна здійснити звернули до таблиць або простеживши криві функцій для заданих значень.
Властивості тангенсоїди та котангенсоїди
Графіки функцій тангенсу та котангенсу значно відрізняються від синусоїди та косинусоїди. Величини tg та ctg є зворотними один одному.


- Y = tg x.
- Тангенсоіда прагне значень y при x = π/2 + πk, але ніколи не досягає їх.
- Найменший позитивний період тангенсоіди дорівнює π.
- Tg (-x) = - tg x, тобто функція непарна.
- Tg x = 0 при x = πk.
- Функція є зростаючою.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Похідна (tg x)' = 1/cos 2 x .
Розглянемо графічне зображення котангенсоіди нижче за текстом.

Основні властивості котангенсоіди:
- Y = ctg x.
- На відміну від функцій синуса і косинуса, в тангенсоіді Y може набувати значення безлічі всіх дійсних чисел.
- Котангенсоіда прагне значень y при x = πk, але ніколи не досягає їх.
- Найменший позитивний період котангенсоіди дорівнює π.
- Ctg (-x) = - ctg x, тобто функція непарна.
- Ctg x = 0, при x = π/2 + πk.
- Функція є спадною.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Похідна (ctg x)’ = — 1/sin 2 x Виправити



