Довести безперервність функції на всій числовій прямій. Як вивчити функцію на безперервність? Безперервність основних елементарних функцій

Безперервна функціяє функцією без «стрибків», тобто таку, на яку виконується умова: малим змінам аргументу слідують малі зміни відповідних значень функції. Графік подібної функції є плавною або безперервною кривою.

Безперервність у точці, граничної для деякої множини, можна визначити за допомогою поняття межі, а саме: функція повинна мати в цій точці межу, яка дорівнює її значенню в граничній точці.

При порушенні цих умов у певній точці говорять, що функція в даній точці зазнає розриву, тобто її безперервність порушується. На мові меж точку розриву можна описати як розбіжність значення функції у розривній точці з межею функції (якщо вона існує).

Точка розриву може бути усувною, для цього необхідне існування межі функції, але не збігається з його значенням заданій точці. І тут її у цій точці можна «поправити», тобто довизначити до безперервності.
Зовсім інша картина складається, якщо межі функції заданої існує. Можливо два варіанти точок розриву:

• першого роду - є і кінцеві обидва з односторонніх меж, і значення одного з них або обох не збігаються зі значенням функції заданої точки;
• другого роду, коли не існує одна або обидві з односторонніх меж або їх значення нескінченні.

Властивості безперервних функцій

• Функція, отримана в результаті арифметичних дій, а також суперпозиції безперервних функцій на їхній області визначення також є безперервною.
• Якщо дана безперервна функція, яка позитивна у певній точці, завжди можна знайти досить малу її околиця, де вона збереже свій знак.
• Аналогічно, якщо її значення у двох точках A і B рівні, відповідно, a і b, причому a відмінно від b, то для проміжних точок вона набуде всіх значень з проміжку (a ; b). Звідси можна зробити цікавий висновок: якщо дати розтягнутій гумці стиснутись так, щоб вона не провисала (залишалася прямолінійною), то одна з її точок залишиться нерухомою. А геометрично це означає, що існує пряма, яка проходить через будь-яку проміжну точку між A та B, яка перетинає графік функції.

Зазначимо деякі з безперервних (на області визначення) елементарних функцій:

• постійна;
• раціональна;
• тригонометричні.

Між двома фундаментальними поняттями в математиці – безперервністю та диференційністю – існує нерозривний зв'язок. Досить згадати, що з диференційованості функції необхідно, щоб це була безперервна функція.

Якщо ж функція у певній точці диференційована, там вона безперервна. Проте зовсім не обов'язково, щоб і її похідна була безперервною.

Функція, що має на деякому безлічі безперервну похідну, належить окремому класу гладких функцій. Інакше висловлюючись, це - безперервно диференційована функція. Якщо ж похідна має обмежену кількість точок розриву (тільки першого роду), то таку функцію називають шматково гладкою.

Ще одним важливим поняттямє рівномірна безперервність функції, тобто її здатність бути у будь-якій точці своєї області визначення однаково безперервної. Таким чином, це властивість, що розглядається на безлічі точок, а не в будь-якій окремо взятій.

Якщо ж зафіксувати точку, то вийде нічим іншим, як визначення безперервності, тобто із наявності рівномірної безперервності випливає, що маємо безперервна функція. Взагалі кажучи, зворотне затвердженнянеправильно. Однак згідно з теоремою Кантора, якщо функція безперервна на компакті, тобто на замкнутому проміжку, вона на ньому рівномірно безперервна.

Визначення.Нехай функція у = f(x) визначена в точці x0 та деякої її околиці. Функція у = f(x) називається безперервний у точці x0, якщо:

1. існує
2. ця межа дорівнює значеннюфункції у точці x0:

При визначенні межі підкреслювалося, що f(x) може бути не визначена в точці x0, а якщо вона визначена в цій точці, то значення f(x0) не бере участі у визначенні межі. При визначенні безперервності важливо, що f(x0) існує, і це значення має дорівнювати lim f(x).

Визначення.Нехай функція у = f(х) визначена в точці x0 та деякої її околиці. Функція f(x) називається безперервною у точці x0, якщо для всіх ε>0 існує додатне числоδ, таке що всім x з δ-околиці точки x0 (тобто.х-x0|
Тут враховується, що значення межі має дорівнювати f(x0), тому, порівняно з визначенням межі, знято умову проколотості δ-околиці 0
Дамо ще одне (рівносильне попереднім) визначення у термінах прирощень. Позначимо Δх = x - x0, цю величину називатимемо збільшенням аргументу. Оскільки х->x0, то Δх->0, тобто Δх - б.м. (Безмежно мала) величина. Позначимо Δу = f(х)-f(x0), цю величину називатимемо збільшенням функції, оскільки |Δу| має бути (при досить малих | Δх |) менше довільного числаε>0, то Δу- теж б.м. величина, тому

Визначення.Нехай функція у = f(х) визначена в точці x0 та деякої її околиці. Функція f(х) називається безперервний у точці x0якщо нескінченно малому прирощенню аргументу відповідає нескінченно мале прирощення функції.

Визначення.Функція f(х), яка не є безперервною в точці x0, називається розривноюу цій точці.

Визначення.Функція f(х) називається безперервною на множині X, якщо вона безперервна в кожній точці цієї множини.

Теорема про безперервність суми, твору, приватного

Теорема про перехід до межі під знаком безперервної функції

Теорема про безперервність суперпозиції безперервних функцій

Нехай функція f(x) визначена на відрізку та монотонна на цьому відрізку. Тоді f(x) може мати у цьому відрізку лише точки розриву першого роду.

Теорема про проміжне значення.Якщо функція f(x) безперервна на відрізку і в двох точках а і b (a менше b) набуває нерівних значень A = f(a) ≠ В = f(b), то для будь-якого числа С, що лежить між А і В, знайдеться точка c ∈ , у якій значення функції дорівнює С: f(c) = C.

Теорема про обмеженість безперервної функції на відрізку.Якщо функція f(x) безперервна на відрізку, вона обмежена у цьому відрізку.

Теорема про досягнення мінімального та максимального значень.Якщо функція f(x) безперервна на відрізку, вона досягає цьому відрізку свої нижню і верхню грані.

Теорема про безперервність зворотної функції.Нехай функція y = f (x) безперервна і строго зростає (зменшується) на відрізку [а, b]. Тоді на відрізку існує зворотна функціях = g(y), також монотонно зростаюча (зменшується) і безперервна.

На цьому уроці вчимося встановлювати безперервність функції. Робитимемо це за допомогою меж, причому односторонніх - правого та лівого, які зовсім не страшні, незважаючи на те, що записуються як і .

Але що таке взагалі безперервність функції? Поки ми не дійшли до суворого визначення, найпростіше уявити лінію, яку можна накреслити, не відриваючи олівець від паперу. Якщо така лінія накреслена, вона безперервна. Ця лінія є графіком безперервної функції.

Графічно функція безперервна у точці , якщо її графік не " розривається " у цій точці. Графік такої безперервної функції - показано на малюнку нижче.

Визначення безперервності функції через межу.Функція є безперервною у точці за дотримання трьох умов:

1. Функція визначена у точці .

Якщо хоча б жодної з перерахованих умов не дотримано, функція не є безперервною в точці. При цьому говорять, що функція зазнає розриву, а точки на графіку, в яких графік переривається, називаються точками розриву функції. Графік такої функції , що зазнає розриву в точці x = 2 - на малюнку нижче.

приклад 1.Функція f(x) визначено наступним чином:

Чи буде ця функція безперервною у кожній з граничних точок її гілок, тобто у точках x = 0 , x = 1 , x = 3 ?

Рішення. Перевіряємо всі три умови безперервності функції у кожній граничній точці. Перше умова дотримується, оскільки те, що функція визначенау кожній з граничних точок, випливає з визначення функції. Залишилося перевірити решту двох умов.

Крапка x= 0. Знайдемо лівосторонню межу в цій точці:

.

Знайдемо правосторонню межу:

x= 0 повинні бути знайдені при тій галузі функції, яка включає в себе цю точку, тобто другої гілки. Знаходимо їх:

Як бачимо, межа функції та значення функції у точці x= 0 рівні. Отже, функція є безперервною у точці x = 0 .

Крапка x= 1. Знайдемо лівосторонню межу в цій точці:

Знайдемо правосторонню межу:

Межа функції та значення функції у точці x= 1 повинні бути знайдені при тій галузі функції, яка включає в себе цю точку, тобто другої гілки. Знаходимо їх:

.

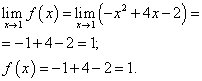Межа функції та значення функції у точці x= 1 рівні. Отже, функція є безперервною у точці x = 1 .

Крапка x= 3. Знайдемо лівосторонню межу в цій точці:

Знайдемо правосторонню межу:

Межа функції та значення функції у точці x= 3 повинні бути знайдені при тій галузі функції, яка включає в себе цю точку, тобто другої гілки. Знаходимо їх:

.

Межа функції та значення функції у точці x= 3 рівні. Отже, функція є безперервною у точці x = 3 .

Основний висновок: дана функціяє безперервною у кожній граничній точці.

Встановити безперервність функції в точці самостійно, а потім переглянути рішення

Безперервна зміна функції можна визначити як поступова зміна, без стрибків, при якому мала зміна аргументу тягне за собою малу зміну функції .

Проілюструємо це безперервна змінафункції з прикладу.

Нехай над столом висить на нитці вантаж. Під дією цього вантажу нитка розтягується, тому відстань lвантажу від точки підвісу нитки є функцією маси вантажу m, тобто l = f(m) , m≥0 .

Якщо трохи змінити масу вантажу, то відстань lзміниться мало: малим змінам mвідповідають малі зміни l. Однак якщо маса вантажу близька до межі міцності нитки, то невелике збільшення маси вантажу може спричинити розрив нитки: відстань lстрибкоподібно збільшиться і дорівнюватиме відстані від точки підвісу до поверхні столу. Графік функції l = f(m) зображений малюнку. На ділянці цей графік є безперервною (суцільною) лінією, а точці він переривається. В результаті виходить графік, що складається із двох гілок. У всіх точках, крім , функція l = f(m) безперервна, а точці вона має розрив.

Дослідження функції на безперервність може бути як самостійним завданням, так і одним з етапів повного дослідження функції та побудови її графіка.

Безперервність функції на проміжку

Нехай функція y = f(x) визначена в інтервалі] a, b[ і безперервна у кожній точці цього інтервалу. Тоді вона називається безперервною в інтервалі] a, b[ . Аналогічно визначається поняття безперервності функції на проміжках виду ]- ∞, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Нехай тепер функція y = f(x) визначено на відрізку [ a, b]. Різниця між інтервалом та відрізком: граничні точки інтервалу не входять до інтервалу, а граничні точки відрізка входять у відрізок. Тут слід згадати про так звану односторонню безперервність: у точці a, залишаючись на відрізку [ a, b] , ми можемо наближатися тільки праворуч, а до точки b- Тільки зліва. Функція називається безперервною на відрізку [ a, b] , якщо вона безперервна у всіх внутрішніх точкахцього відрізка, безперервна праворуч у точці aі безперервна зліва в точці b.

Прикладом безперервної функції може бути будь-яка з елементарних функцій. Кожна елементарна функція безперервна будь-якому відрізку, у якому вона визначена. Наприклад, функції та безперервні на будь-якому відрізку [ a, b] , функція безперервна на відрізку [ 0 , b] , функція безперервна на будь-якому відрізку, що не містить точку a = 2 .

приклад 4.Дослідити функцію на безперервність.

Рішення. Перевіряємо першу умову. Функція не визначена в точках - 3 і 3. Щонайменше одна з умов безперервності функції на всій числовій прямій не виконується. Тому ця функція є безперервною на інтервалах

Приклад 5.Визначити, за якого значення параметра aбезперервна на всій області визначенняфункція

Рішення.

Знайдемо правосторонню межу при:

.

Очевидно, що значення у точці x= 2 має бути рівним ax :

a = 1,5 .

Приклад 6.Визначити, за яких значень параметрів aі bбезперервна на всій області визначенняфункція

Рішення.
Знайдемо лівосторонню межу функції в точці:

.

Отже, значення в точці має дорівнювати 1:

Знайдемо лівосторонній функції в точці:

Очевидно, що значення функції в точці має дорівнювати :

Відповідь: функція безперервна на всій області визначення при a = 1; b = -3 .

Основні властивості безперервних функцій

До поняття безперервної функції математика дійшла, вивчаючи насамперед різні закони руху. Простір і час нескінченні, і залежність, наприклад, шляхи sвід часу t, виражена законом s = f(t) , дає приклад безперервної функції f(t). Безперервно змінюється і температура води, що нагрівається, вона також є безперервною функцією від часу: T = f(t) .

У математичний аналіздоведені деякі властивості, які мають безперервні функції. Наведемо найважливіші з цих властивостей.

1. Якщо безперервна на інтервалі функція набирає на кінцях інтервалу значення різних знаків, то в деякій точці цього відрізка вона набуває значення, рівне нулю. У формальному викладі це властивість дано в теоремі, відомої як перша теорема Больцано-Коші.

2. Функція f(x) , безперервна на інтервалі [ a, b] , приймає всі проміжні значення між значеннями в кінцевих точках, тобто між f(a) та f(b). У формальному викладі це властивість дано в теоремі, відомої як друга теорема Больцано-Коші.

Розглянемо дві функції, графіки яких зображено на рис. 1 та 2. Графік першої функції можна намалювати, не відриваючи олівця від паперу. Цю функцію можна назвати безперервною. Графік іншої функції так намалювати не можна. Він складається із двох безперервних шматків, а в точці має розрив, і функцію ми назвемо розривною.

Таке наочне визначення безперервності ніяк не може влаштувати математику, оскільки містить зовсім нематематичні поняття «олівець» та «папір». Точне математичне визначеннябезперервності дається на основі поняття межі та полягає в наступному.

Нехай функція визначена на відрізку і деяка точка цього відрізка. Функція називається безперервною у точці , якщо за прагненні ( розглядається лише з відрізка ) значення функції прагнуть , тобто . якщо

. (1)

Функція називається безперервною на відрізку, якщо вона безперервна у кожній його точці.

Якщо у точці рівність (1) не виконується, функція називається розривною у точці .

Як бачимо, математично властивість безперервності функції на відрізку визначається через місцеву (локальну) властивість безперервності в точці.

Розмір називається збільшенням аргументу, різниця значень функції називається збільшенням функції і позначається . Вочевидь, що з прагненні до збільшення аргументу прагне нулю: .

Перепишемо рівність (1) у рівносильному вигляді

.

Використовуючи введені позначення, його можна переписати так:

Отже, якщо функція безперервна, то при прагненні збільшення аргументу до нуля збільшення функції прагне до нуля. Говорять і інакше: малому прирощенню аргументу відповідає мале збільшення функції. На рис. 3 наведено графік безперервної у точці функції, прирощенню відповідає збільшення функції . На рис. 4 приросту відповідає таке збільшення функції , яке, як би мало не було, не буде менше половини довжини відрізка ; функція розривна в точці.

Наше уявлення про безперервну функцію як про функцію, графік якої можна намалювати, не відриваючи олівця від паперу, чудово підтверджується властивостями безперервних функцій, які доводяться в математичному аналізі. Зазначимо, наприклад, такі властивості.

1. Якщо безперервна на відрізку функція приймає на кінцях відрізка значення різних знаків, то деякій точці цього відрізка вона приймає значення, що дорівнює нулю.

2. Функція , безперервна на відрізку , приймає всі проміжні значення між значеннями кінцевих точках, тобто. між та .

3. Якщо функція безперервна на відрізку, то на цьому відрізку вона досягає свого найбільшого та свого найменшого значення, тобто. якщо - найменше, а - найбільше значення функції на відрізку , то знайдуться цьому відрізку такі точки і , як і .

Геометричний зміст першого з цих тверджень абсолютно зрозумілий: якщо безперервна крива переходить з одного боку осі на іншу, вона перетинає цю вісь (рис. 5). Розривна функція цією властивістю не має, що підтверджується графіком функції на рис. 2, а також властивостями 2 та 3. На рис. 2 функція не набуває значення, хоча воно укладено між і. На рис. 6 наведено приклад розривної функції ( дрібна частиначисла ), яка не досягає свого найбільшого значення.

Додавання, віднімання, множення безперервних одному й тому відрізку функцій знову призводять до безперервним функцій. При розподілі двох безперервних функцій вийде безперервна функція, якщо знаменник скрізь відмінний від нуля.

До поняття безперервної функції математика дійшла, вивчаючи насамперед різні закони руху. Простір і час безперервні, і залежність, наприклад, шляху від часу, виражена законом, дає приклад безперервної функції.

За допомогою безперервних функцій описують стани та процеси у твердих тілах, рідинах та газах. Вивчають їх науки – теорія пружності, гідродинаміка та аеродинаміка – об'єднуються однією назвою – «механіка суцільного середовища».