Як визначити невизначений інтеграл. Рішення інтеграла онлайн

I. Вирази, у яких поряд із літерами можуть бути використані числа, знаки арифметичних дійі дужки, називаються виразами алгебри.

Приклади виразів алгебри:

2m-n; 3 · (2a + b); 0,24x; 0,3a -b · (4a + 2b); a 2 - 2ab;

Так як букву в алгебраїчному виразі можна замінити якимись різними числами, то букву називають змінною, а саме алгебраїчний вираз- Виразом зі змінною.

ІІ. Якщо в алгебраїчному вираженні літери (змінні) замінити їх значеннями та виконати зазначені дії, то отримане в результаті число називається значенням виразу алгебри.

приклади. Знайти значення виразу:

1) a + 2b -c при a = -2; b = 10; c = -3,5.

2) | + | y ​​| -|z| при х = -8; y = -5; z = 6.

Рішення.

1) a + 2b -c при a = -2; b = 10; c = -3,5. Замість змінних підставимо їх значення. Отримаємо:

— 2+ 2 · 10- (-3,5) = -2 + 20 +3,5 = 18 + 3,5 = 21,5.

2) | + | y ​​| -|z| при x = -8; y = -5; z = 6. Підставляємо вказані значення. Пам'ятаємо, що модуль негативного числадорівнює протилежному йому числу, а модуль позитивного числадорівнює самому цьому числу. Отримуємо:

|-8| + |-5| -|6| = 8 + 5 -6 = 7.

ІІІ.Значення літери (змінної), у яких алгебраїчне вираз має сенс, називають допустимими значеннями літери (змінної).

приклади. При яких значеннях змінної виразне має сенсу?

Рішення.Ми знаємо, що на нуль ділити не можна, тому кожне з цих виразів не матиме сенсу при тому значенні літери (змінної), яка звертає знаменник дробу в нуль!

У прикладі 1) це значення а = 0. Справді, якщо замість а підставити 0, потрібно буде число 6 ділити на 0, а цього робити не можна. Відповідь: вираз 1) немає сенсу при а = 0.

У прикладі 2) знаменник х - 4 = 0 при х = 4, отже, це значення х = 4 і не можна брати. Відповідь: вираз 2) немає сенсу при х = 4.

У прикладі 3) знаменник х + 2 = 0 за х = -2. Відповідь: вираз 3) немає сенсу при х = -2.

У прикладі 4) знаменник 5-|x| = 0 за |x| = 5. Оскільки |5| = 5 та |-5| = 5, то не можна брати х = 5 та х = -5. Відповідь: вираз 4) немає сенсу при х = -5 і за х = 5.
IV. Два вирази називаються тотожно рівними, якщо за будь-яких допустимих значенняхЗмінні відповідні значення цих виразів рівні.

Приклад: 5 (a – b) і 5a – 5b теж однакові, оскільки рівність 5 (a – b) = 5a – 5b буде вірним за будь-яких значеннях a і b. Рівність 5 (a – b) = 5a – 5b є тотожністю.

Тотожність – це рівність, справедливе за всіх допустимих значеннях змінних, що входять до нього. Прикладами вже відомих вам тотожностей є, наприклад, властивості додавання та множення, розподільна властивість.

Заміну одного виразу іншим, тотожно рівним йому виразом, називають тотожним перетворенням або просто перетворенням виразу. Тотожні перетворення виразів зі змінними виконуються з урахуванням властивостей дій над числами.

приклади.

a)перетворіть вираз у тотожно рівну, використовуючи розподільну властивість множення:

1) 10 · (1,2 х + 2,3у); 2) 1,5 · (a -2b + 4c); 3) a · (6m -2n + k).

Рішення. Згадаймо розподільну властивість (закон) множення:

(a+b)·c=a·c+b·c(розподільний закон множення щодо додавання: щоб суму двох чисел помножити на третє число, можна кожне доданок помножити на це число та отримані результати скласти).
(а-b)·c=a·с-b·c(розподільний закон множення щодо віднімання: щоб різницю двох чисел помножити на третє число, можна помножити на це число, що зменшується і віднімається окремо і з першого результату відняти другий).

1) 10 · (1,2 х + 2,3у) = 10 · 1,2 х + 10 · 2,3у = 12х + 23у.

2) 1,5 · (a -2b + 4c) = 1,5а -3b + 6c.

3) a · (6m -2n + k) = 6am -2an + ak.

б)перетворіть вираз у тотожно рівну, використовуючи переміщувальну та поєднувальну властивості (закони) складання:

4) х+4,5+2х+6,5; 5) (3а + 2,1) + 7,8; 6) 5,4 с -3 -2,5 -2,3 с.

Рішення.Застосуємо закони (властивості) складання:

a+b=b+a(переміщувальний: від перестановки доданків сума не змінюється).
(a+b)+c=a+(b+c)(Сполучний: щоб до суми двох доданків додати третє число, можна до першого числа додати суму другого та третього).

4) х + 4,5 +2х + 6,5 = (х + 2х) + (4,5 + 6,5) = 3х + 11.

5) (3а + 2,1) + 7,8 = 3а + (2,1 + 7,8) = 3а + 9,9.

6) 6) 5,4 с -3 -2,5 -2,3 с = (5,4 с -2,3 с) + (-3 -2,5) = 3,1 с -5,5.

в)перетворіть вираз у тотожно рівне, використовуючи переміщувальну та поєднувальну властивості (закони) множення:

7) 4 · х · (-2,5); 8) -3,5 · 2у · (-1); 9) 3а · (-3) · 2с.

Рішення.Застосуємо закони (властивості) множення:

a b = b a(Перемістковий: від перестановки множників твір не змінюється).
(a·b)·c=a·(b·c)(Сполучний: щоб добуток двох чисел помножити на третє число, можна перше число помножити на твір другого та третього).

7) 4 · х · (-2,5) = -4 · 2,5 · х = -10х.

8) -3,5 · 2у · (-1) = 7у.

9) 3а · (-3) · 2с = -18ас.

Якщо алгебраїчне вираз дано як скоротливої ​​дробу, то користуючись правилом скорочення дробу його можна спростити, тобто. замінити тотожно рівним йому простішим виразом.

приклади. Спростіть за допомогою скорочення дробів.

Рішення.Скоротити дріб - це означає розділити її чисельник і знаменник на те саме число (вираз), відмінне від нуля. Дроб 10) скоротимо на 3b; дріб 11) скоротимо на аі дріб 12) скоротимо на 7n. Отримуємо:

Алгебраїчні вирази застосовують для складання формул.

Формула – це вираз алгебри, записаний у вигляді рівності і виражає залежність між двома або декількома змінними.Приклад: відома вам формула шляху s=v·t(s - пройдений шлях, v - швидкість, t - час). Згадайте, які формули ви знаєте.

Сторінка 1 з 1 1

За допомогою будь-якої мови можна висловити ту саму інформацію різними словамита оборотами. Не є винятком і математична мова. Але те саме вираз можна еквівалентним чином записати по-різному. І в деяких ситуаціях один із записів є більш простим. Про спрощення висловлювань ми й поговоримо на цьому уроці.

Люди спілкуються на різних мовах. Для нас важливим порівнянням є пара «російська - математична мова». Одну й ту саму інформацію можна повідомити різними мовами. Але, крім цього, її можна і однією мовою вимовити по-різному.

Наприклад: «Петя товаришує з Васею», «Вася товаришує з Петею», «Петя з Васею друзі». Сказано по-різному, але те саме. За будь-якою з цих фраз ми зрозуміли б, про що йдеться.

Давайте подивимося таку фразу: «Хлопчик Петя і хлопчик Вася дружать». Ми зрозуміли, про що йде мова. Проте нам не подобається, як звучить ця фраза. Чи не можемо ми її спростити, сказати те саме, але простіше? «Хлопчик і хлопчик» - можна один раз сказати: «Хлопчики Петя і Вася дружать».

Хлопчики ... Хіба за іменами не зрозуміло, що вони не дівчатка. Прибираємо «хлопчики»: «Петя та Вася дружать». А слово «дружать» можна замінити на «друзі»: «Петя та Вася – друзі». У результаті першу, довгу негарну фразу замінили еквівалентним висловлюванням, яке простіше сказати та простіше зрозуміти. Ми спростили цю фразу. Спростити - означає сказати простіше, але не втратити, не спотворити сенс.

У математичною мовоювідбувається приблизно те саме. Одне й те саме можна сказати, записати по-різному. Що означає спростити вираз? Це означає, що з вихідного висловлювання існує безліч еквівалентних виразів, тобто тих, що означають те саме. І з усієї цієї множини ми повинні вибрати найпростіше, на наш погляд, чи найпридатніше для наших подальших цілей.

Наприклад, розглянемо числове вираз . Йому еквівалентне буде.

Також буде еквівалентно першим двом: .

Виходить, що ми спростили наші вирази і знайшли найкоротший еквівалентний вираз.

Для числових виразівзавжди потрібно виконувати всі дії та отримувати еквівалентний вираз у вигляді одного числа.

Розглянемо приклад літерного виразу . Очевидно, що простіше буде.

При спрощенні буквених виразівнеобхідно виконати всі дії, які можливі.

Чи завжди потрібно спрощувати вираз? Ні, іноді нам зручніше буде еквівалентний, але довший запис.

приклад: від числа потрібно відібрати число .

Обчислити можна, але якби перше число було представлено своїм еквівалентним записом: , то обчислення були миттєвими: .

Тобто спрощене вираження не завжди нам вигідне для подальших обчислень.

Проте дуже часто ми стикаємося із завданням, яке так і звучить «спростити вираз».

Спростити вираз: .

Рішення

1) Виконаємо дії у перших та у других дужках: .

2) Обчислимо твори: .

Очевидно, останній вираз має простіший вигляд, ніж початковий. Ми його спростили.

Щоб спростити вираз, його необхідно замінити на еквівалентне (рівне).

Для визначення еквівалентного виразу необхідно:

1) виконати всі можливі дії,

2) користуватися властивостями додавання, віднімання, множення та поділу для спрощення обчислень.

Властивості додавання та віднімання:

1. Переміщувальна властивістьдодавання: від перестановки доданків сума змінюється.

2. Сполучна властивістьскладання: щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого та третього числа.

3. Властивість віднімання суми з числа: щоб відняти суму з числа, можна віднімати кожен доданок окремо.

Властивості множення та поділу

1. Переміщувальна властивість множення: від перестановки множників твір не змінюється.

2. Сполучна властивість: щоб помножити число на добуток двох чисел, можна спочатку помножити його на перший множник, а потім отриманий добуток помножити на другий множник.

3. Розподільча властивістьмноження: щоб число помножити на суму, потрібно його помножити на кожен доданок окремо.

Подивимося, як ми насправді робимо обчислення в умі.

Обчисліть:

Рішення

1) Уявимо як

2) Представимо перший множник як суму розрядних доданківі виконаємо множення:

3) можна уявити як і виконати множення:

4) Замінимо перший множник еквівалентною сумою:

Розподільний закон можна використовувати і в зворотний бік: .

Виконайте дії:

1) 2)

Рішення

1) Для зручності можна скористатися розподільчим законом, тільки використовувати його у зворотний бік – винести загальний множникза дужки.

2) Винесемо за дужки загальний множник

Необхідно купити лінолеум на кухню та передпокій. Площа кухні - , вітальні - . Є три види лінолеумів: по , і за . Скільки буде коштувати кожен з трьох видівлінолеуму? (Мал. 1)

Мал. 1. Ілюстрація до умови завдання

Рішення

Спосіб 1. Можна окремо знайти, скільки грошей потрібно на купівлю лінолеуму на кухню, а потім у передпокій та отримані твори скласти.

Знайти невизначений інтеграл (безліч первісних або "антипохідних") означає відновити функцію за відомою похідною цієї функції. Відновлена ​​безліч первісних F(x) + З для функції f(x) враховує константу інтегрування C. За швидкістю переміщення матеріальної точки(похідною) може бути відновлено закон руху цієї точки (первоподібна); щодо прискорення руху точки - її швидкість та закон руху. Як бачимо, інтегрування - широке полі діяльності Шерлоков Холмсов від фізики. Та й в економіці багато понять надаються через функції та їх похідні і тому, наприклад, можна за продуктивністю праці у певний момент часу (похідної) відновити обсяг продукції, випущений у відповідний час.

Щоб знайти невизначений інтеграл, потрібна досить невелика кількість основних формул інтегрування. Але процес його знаходження значно важче, ніж лише застосування цих формул. Вся складність відноситься не до інтегрування, а до приведення інтегрованого виразу до такого виду, який дає можливість знайти невизначений інтеграл за вищезазначеними основними формулами. Це означає, що для початку практики інтегрування потрібно активізувати отримані в середній школінавички перетворення виразів.

Вчитися знаходити інтеграли будемо, користуючись властивостями та таблицею невизначених інтегралівз уроку про основні поняття цієї теми (відкриється у новому вікні).

Існує кілька методів знаходження інтеграла, з яких метод заміни змінноїі метод інтегрування частинами- обов'язковий джентльменський набір кожного, хто успішно здав найвищу математику. Однак починати освоювати інтегрування корисніше і приємніше із застосуванням методу розкладання, заснованому на двох теоремах про властивості невизначеного інтеграла, які для зручності повторимо тут.

Теорема 3.Постійний множник у подинтегральном вираженні можна виносити за знак невизначеного інтеграла, тобто.

Теорема 4.Невизначений інтеграл суми алгебри кінцевого числафункцій дорівнює алгебраїчній суміневизначених інтегралів цих функцій, тобто.

(2)

Крім того, в інтегруванні може стати в нагоді наступне правило: якщо вираз підінтегральної функції містить постійний множник, то вираз первісної домножується на число, зворотне постійному множнику, тобто

(3)

Оскільки цей урок - вступний у вирішення завдань інтегрування, важливо відзначити дві речі, які або вже насправді початковому етапіабо трохи пізніше можуть вас здивувати. Здивування пов'язане з тим фактом, що інтегрування - операція, зворотна диференціюванню і невизначений інтеграл можна справедливо називати "антипохідною".

Перша річ, якою не слід дивуватися при інтегруванні.У таблиці інтегралів існують формули, які не мають аналогів серед формул похідної таблиці . Це такі формули:

Однак можна переконатися в тому, що похідні виразів, що стоять у правих частинах цих формул, збігаються з відповідними підінтегральними функціями.

Друга річ, якій не слід дивуватися при інтегруванні. Хоча похідна будь-якої елементарної функції є також елементарною функцією, невизначені інтеграли від деяких елементарних функцій не є елементарними функціями . Прикладами таких інтегралів можуть бути такі:

Для вироблення техніки інтегрування стануть у нагоді такі навички: скорочення дробів, розподіл багаточлена в чисельнику дробу на одночлен у знаменнику (для отримання суми невизначених інтегралів), перетворення коренів у ступені, множення одночлена на багаточлен, зведення в ступінь. Ці навички потрібні для перетворень підінтегрального виразу, у яких має вийти сума інтегралів, присутніх у таблиці інтегралів.

Знаходимо невизначені інтеграли разом

приклад 1.Знайти невизначений інтеграл

.

Рішення. Бачимо у знаменнику підінтегрального виразу багаточлен, у якому ікс у квадраті. Це майже вірна ознака того, що можна застосувати табличний інтеграл 21 (з арктангенсом у результаті). Виносимо із знаменника множник-двійку (є така властивість інтеграла - постійний множник можна виносити за знак інтеграла, вище воно було згадано як теорема 3). Результат всього цього:

Тепер у знаменнику є сума квадратів, а це означає, що можемо застосувати згаданий табличний інтеграл. Остаточно отримуємо відповідь:

.

приклад 2.Знайти невизначений інтеграл

Рішення. Знову застосовуємо теорему 3 - властивість інтеграла, на підставі якого постійний множник можна виносити за знак інтеграла:

Застосовуємо формулу 7 з таблиці інтегралів (змінна до ступеня) до підінтегральної функції:

.

Скорочуємо дроби і перед нами кінцева відповідь:

приклад 3.Знайти невизначений інтеграл

Рішення. Застосовуючи спочатку теорему 4, а потім теорему 3 про властивості знайдемо даний інтеграл як суму трьох інтегралів:

Усі три отримані інтеграли – табличні. Використовуємо формулу (7) з таблиці інтегралів при n = 1/2, n= 2 і n= 1/5, і тоді

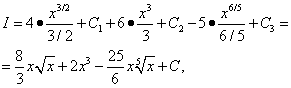
об'єднує всі три довільні постійні, які були введені при знаходженні трьохінтегралів. Тому в аналогічних ситуаціяхслід вводити лише одну довільну постійну (константу) інтегрування.

приклад 4.Знайти невизначений інтеграл

Рішення. Коли знаменнику подинтегральной дробу - одночлен, можемо почленно розділити чисельник на знаменник. Вихідний інтеграл перетворився на суму двох інтегралів:

.

Щоб застосувати табличний інтеграл, перетворимо коріння в міру і ось вже остаточна відповідь:

Продовжуємо знаходити невизначені інтеграли разом

Приклад 7.Знайти невизначений інтеграл

Рішення. Якщо ми перетворимо підінтегральну функцію, звівши двочлен у квадрат і розділивши почленно чисельник на знаменник, то вихідний інтеграл стане сумою трьох інтегралів.