Інтеграл від синус ікс у квадраті. Інтегрування тригонометричних функцій: методи та приклади

Розглянемо інтеграли, в яких підінтегральна функція є твір синусів і косінусів першого ступеня від іксу, помноженого на різні множники, тобто інтеграли виду

Скориставшись відомими тригонометричними формулами

(2)
(3)
(4)
можна перетворити кожен із творів в інтегралах виду (31) в алгебраїчну сумута проінтегрувати за формулами

(5)

(6)

приклад 1.Знайти

Рішення. За формулою (2) при

приклад 2.Знайти інтеграл від тригонометричної функції

Рішення. За формулою (3) при

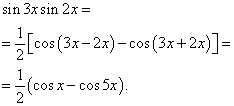
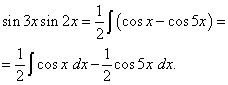
приклад 3.Знайти інтеграл від тригонометричної функції

Рішення. За формулою (4) при отримуємо наступне перетворення підінтегрального виразу:

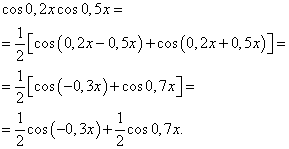
Застосовуючи формулу (6), отримаємо

Інтеграл твору ступенів синуса та косинуса одного і того ж аргументу

Розглянемо тепер інтеграли від функцій, які є твір ступенів синуса і косинуса однієї й тієї ж аргументу, тобто.

(7)

У окремих випадках один із показників ( mабо n) може дорівнювати нулю.

При інтегруванні таких функцій використовують те, що парний ступінь косинуса можна виразити через синус, а диференціал синуса дорівнює cos x dx(або парний ступінь синуса можна виразити через косинус, а диференціал косинуса дорівнює - sin x dx ) .

Слід розрізняти два випадки: 1) хоча б один із показників mі nнепарний; 2) обидва показники парні.

Нехай має місце перший випадок, а саме показник n = 2k+ 1 – непарний. Тоді, враховуючи, що

Подинтегральное вираз представлено у вигляді, що його частина – функція лише синуса, іншу – диференціал синуса. Тепер за допомогою заміни змінної t= sin xрішення зводиться до інтегрування багаточлена щодо t. Якщо ж лише ступінь mнепарна, то чинять аналогічно, виділяючи множник sin x, висловлюючи решту підінтегральної функції через cos xі вважаючи t= cos x. Цей прийом можна використовувати і при інтегруванні приватного ступенів синуса та косинуса , коли хоча б один із показників - непарний . Вся справа в тому, що приватне ступенів синуса та косинуса - це окремий випадокїх твори : коли тригонометрична функція знаходиться в знаменнику підінтегрального виразу, її ступінь - негативний. Але бувають і випадки приватного тригонометричних функцій, коли їх ступеня - лише парні. Про них – наступний абзац.

Якщо ж обидва показники mі n– парні, то, використовуючи тригонометричні формули

знижують показники ступеня синуса та косинуса, після чого вийде інтеграл того самого типу, що й вище. Тому інтегрування слід продовжувати за тією самою схемою. Якщо ж один із парних показників- негативний, тобто розглядається приватне парних ступенів синуса та косинуса, то дана схемане підходить . Тоді використовується заміна змінної залежно від цього, як можна перетворити подынтегральное вираз. Такий випадок буде розглянуто у наступному параграфі.

приклад 4.Знайти інтеграл від тригонометричної функції

Рішення. Показник ступеня косинуса – непарний. Тому уявімо

t= sin x(тоді dt= cos x dx ). Тоді отримаємо

Повертаючись до старої змінної, остаточно знайдемо

Приклад 5.Знайти інтеграл від тригонометричної функції

Рішення. Показник ступеня косинуса, як і попередньому прикладі – непарний, але більше. Уявимо

і зробимо заміну змінної t= sin x(тоді dt= cos x dx ). Тоді отримаємо

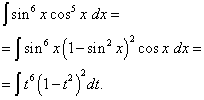
Розкриємо дужки

і отримаємо

Повертаючись до старої змінної, отримуємо рішення

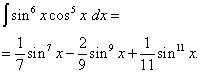
Приклад 6.Знайти інтеграл від тригонометричної функції

Рішення. Показники ступеня синуса та косинуса – парні. Тому перетворимо підінтегральну функцію так:

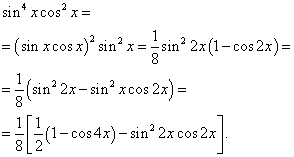
Тоді отримаємо

У другому інтегралі зробимо заміну змінної, вважаючи t= sin2 x. Тоді (1/2)dt= cos2 x dx . Отже,

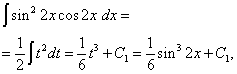
Остаточно отримуємо

Використання методу заміни зміною

Метод заміни змінноїпри інтегруванні тригонометричних функцій можна застосовувати у випадках, коли в підінтегральному вираженні присутній тільки синус або тільки косинус, добуток синуса і косинуса, в якому або синус або косинус - в першому ступені, тангенс або котангенс, а також приватне парних ступенів синуса і косинуса одного і того ж аргументу. При цьому можна проводити перестановки не тільки в sin x = tі sin x = t, Але і tg x = tта ctg x = t .

Приклад 8.Знайти інтеграл від тригонометричної функції

Рішення. Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, легко інтегрується за таблицею інтегралів:

Приклад 9.Знайти інтеграл від тригонометричної функції

Рішення. Перетворюємо тангенс у відношенні синуса та косинуса:

Зробимо заміну змінної: , Тоді . Підинтегральний вираз, що вийшов, являє собою табличний інтегралзі знаком мінус:

Повертаючись до початкової змінної, остаточно отримуємо:

приклад 10.Знайти інтеграл від тригонометричної функції

Рішення. Зробимо заміну змінної: , Тоді .

Перетворимо підінтегральний вираз, щоб застосувати тригонометричну тотожність :

Здійснюємо заміну змінної, не забуваючи перед інтегралом поставити знак мінус (дивіться вище, чому одно dt). Далі розкладаємо підінтегральний вираз на множники та інтегруємо за таблицею:

Повертаючись до початкової змінної, остаточно отримуємо:

Знайти інтеграл від тригонометричної функції самостійно, а потім переглянути рішення

Універсальна тригонометрична підстановка

Універсальну тригонометричну підстановку можна застосовувати у випадках, коли підінтегральний вираз не підпадає під випадки, розібрані у попередніх параграфах. В основному, коли синус або косинус (або те й інше) знаходяться в знаменнику дробу. Доведено, що синус та косинус можна замінити іншим виразом, що містить тангенс половини вихідного кута наступним чином:

Але зауважимо, що універсальна тригонометрична підстановка часто спричиняє досить складні. алгебраїчні перетворенняТому її краще застосовувати, коли ніякий інший метод не працює. Розберемо приклади, коли разом із універсальною тригонометричною підстановкою використовуються підведення під знак диференціалу та метод невизначених коефіцієнтів.

приклад 12.Знайти інтеграл від тригонометричної функції

Рішення. Рішення. Скористаємося універсальною тригонометричною підстановкою. Тоді
.

Дроби в чисельнику та знаменнику множимо на , а двійку виносимо і ставимо перед знаком інтеграла. Тоді

Докладно розглянуті приклади рішень інтегралів частинами, подинтегральное вираз яких є твором многочлена на експоненту (е ступеня х) чи синус (sin x) чи косинус (cos x).

Формула інтегрування частинами

При вирішенні прикладів цього розділу використовується формула інтегрування частинами:
;
.

Приклади інтегралів, що містять добуток багаточлена і sin x, cos x або e x

Ось приклади таких інтегралів:
, , .

Для інтегрування подібних інтегралів, многочлен позначають через u , а частину, що залишилася - через v dx . Далі застосовують формулу інтегрування частинами.

Нижче дається докладне рішенняцих прикладів.

Приклади вирішення інтегралів

Приклад з експонентою, е в ступені х

Визначити інтеграл:
.

Рішення

Введемо експоненту під знак диференціалу:
e - x dx = - e - x d(-x) = - d(e - x).

Інтегруємо частинами.

тут
.
Інтеграл, що залишився, також інтегруємо частинами.
.
.
.
Остаточно маємо:
.

Відповідь

Приклад визначення інтеграла із синусом

Обчислити інтеграл:
.

Рішення

Введемо синус під знак диференціалу:

Інтегруємо частинами.

тут u = x 2 , v = cos(2 x+3), du = ( x 2 )′ dx

Інтеграл, що залишився, також інтегруємо частинами. І тому вводимо косинус під знак диференціала.

тут u = x, v = sin(2 x+3), du = dx

Остаточно маємо:

Відповідь

Приклад твору багаточлена та косинуса

Обчислити інтеграл:
.

Рішення

Введемо косинус під знак диференціалу:

Інтегруємо частинами.

тут u = x 2 + 3 x + 5, v = sin 2 x, du = ( x 2 + 3 x + 5 )′ dx

Раніше ми по заданої функції, керуючись різними формулами та правилами, знаходили її похідну. Похідна має численні застосування: це швидкість руху (або узагальнюючи швидкість протікання будь-якого процесу); кутовий коефіцієнтщо стосується графіку функції; за допомогою похідної можна досліджувати функцію на монотонність та екстремуми; вона допомагає вирішувати завдання оптимізацію.

Але поряд із завданням про знаходження швидкості за відомим законом руху зустрічається і зворотне завдання- завдання про відновлення закону руху по відомої швидкості. Розглянемо одне з таких завдань.

приклад 1.По прямій рухається матеріальна точка, Швидкість її руху в момент часу t задається формулою v = gt. Знайти закон руху.
Рішення. Нехай s = s(t) – шуканий закон руху. Відомо, що s"(t) = v(t). Значить, для вирішення задачі потрібно підібрати функцію s = s(t), похідна якої дорівнює gt. Неважко здогадатися, що $s(t) = \frac(gt^) 2) (2) $.
$s"(t) = \left(\frac(gt^2)(2) \right)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t = gt $
Відповідь: $s(t) = \frac(gt^2)(2) $

Відразу зауважимо, що приклад вирішено правильно, але неповно. Ми отримали $s(t) = \frac(gt^2)(2) $. Насправді завдання має безліч рішень: будь-яка функція виду $s(t) = \frac(gt^2)(2) + C $, де C - довільна константа, може служити законом руху, оскільки $\left (\frac(gt^2)(2) +C \right)" = gt $

Щоб завдання стало більш визначеним, нам треба було зафіксувати вихідну ситуацію: вказати координату точки, що рухається в якийсь момент часу, наприклад при t = 0. Якщо, скажімо, s(0) = s 0 , то з рівності s(t) = (gt 2)/2 + C одержуємо: s(0) = 0 + С, тобто C = s 0 . Тепер закон руху визначено однозначно: s(t) = (gt 2)/2 + s 0 .

У математиці взаємно зворотним операціям надають різні назви, вигадують спеціальні позначення, наприклад: зведення в квадрат (х 2) та витяг квадратного кореня($\sqrt(x) $), синус (sin x) і арксинус (arcsin x) і т. д. Процес знаходження похідної за заданою функцією називають диференціюванням, а зворотну операцію, Т. е. процес знаходження функції за заданою похідною, - інтегруванням.

Сам термін «похідна» можна обґрунтувати «по-житейськи»: функція у = f(x) «виробляє світ» нову функціюу "= f"(x). Функція у = f(x) виступає хіба що як «батька», але математики, природно, не називають її «батьком» чи «виробником», вони кажуть, що це стосовно функції у" = f"(x) , первинний образ, або первісна.

Визначення.Функцію y = F(x) називають первісною для функції y = f(x) на проміжку X, якщо для (x \ in X \) виконується рівність F"(x) = f(x)

Насправді проміжок X зазвичай не вказують, але мають на увазі (як природної області визначення функції).

Наведемо приклади.
1) Функція у = х 2 є первісною для функції у = 2х, оскільки для будь-якого х справедлива рівність (x 2) "= 2х
2) Функція у = х 3 є первісною для функції у = 3х 2, оскільки для будь-якого х справедлива рівність (x 3) "= 3х 2
3) Функція у = sin(x) є первісною для функції y = cos(x), оскільки для будь-якого x справедлива рівність (sin(x))" = cos(x)

При знаходженні первісних, як і похідних, використовуються як формули, а й деякі правила. Вони безпосередньо пов'язані з відповідними правилами обчислення похідних.

Ми знаємо, що похідна сума дорівнює сумі похідних. Це породжує відповідне правило знаходження первісних.

Правило 1.Первісна сума дорівнює сумі первісних.

Ми знаємо, що постійний множникможна винести за знак похідної. Це породжує відповідне правило знаходження первісних.

Правило 2Якщо F(x) - первісна для f(x), то kF(x) - первісна для kf(x).

Теорема 1.Якщо y = F(x) - первісна для функції y = f(x), то першорядною для функції у = f(kx + m) служить функція $y=\frac(1)(k)F(kx+m) $

Теорема 2.Якщо y = F(x) - первісна для функції y = f(x) на проміжку X, то у функції у = f(x) нескінченно багато первісних, і всі вони мають вигляд y = F(x) + C.

Методи інтегрування

Метод заміни змінної (метод підстановки)

Метод інтегрування підстановкою полягає у запровадженні нової змінної інтегрування (тобто підстановки). При цьому заданий інтеграл приводиться до нового інтеграла, який є табличним або зводиться до нього. Загальних методівпідбору підстановок немає. Вміння правильно визначити підстановку набуває практики.
Нехай потрібно обчислити інтеграл $\textstyle \int F(x)dx $. Зробимо підстановку $x= \varphi(t) $ де $\varphi(t) $ - функція, що має безперервну похідну.
Тоді $dx = \varphi "(t) \cdot dt $ і на підставі властивості інваріантності формули інтегрування невизначеного інтеграла отримуємо формулу інтегрування підстановкою:
$\int F(x) dx = \int F(\varphi(t)) \cdot \varphi "(t) dt $

Інтегрування виразів виду $\textstyle \int \sin^n x \cos^m x dx $

Якщо m непарне, m > 0, то зручніше зробити підстановку sin x = t.
Якщо n непарне, n > 0, зручніше зробити підстановку cos x = t.
Якщо n і m парні, зручніше зробити підстановку tg x = t.

Інтегрування частинами

Інтегрування частинами - застосування наступної формули для інтегрування:
$\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du $
або:
$\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx $

Таблиця невизначених інтегралів (первоподібних) деяких функцій

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) + C \; \; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch) ) x + C $$

Для інтегрування раціональних функційвиду R(sin x, cos x) застосовують підстановку, яка називається універсальною тригонометричною підстановкою. Тоді. Універсальна тригонометрична підстановка часто призводить до великих обчислень. Тому, наскільки можна, користуються такими підстановками.

Інтегрування функцій, що раціонально залежать від тригонометричних функцій

1. Інтеграли виду ∫ sin n xdx , ∫ cos n xdx , n>0
a) Якщо n непарне, то один ступінь sinx (або cosx) слід внести під знак диференціала, а від решти парного ступеняслід перейти до протилежної функції.
б) Якщо n парне, то користуємося формулами зниження ступеня
2. Інтеграли виду ∫ tg n xdx , ∫ ctg n xdx , де n – ціле.
Необхідно використовувати формули

3. Інтеграли виду ∫ sin n x·cos m x dx
а) Нехай m і n різної парності. Застосовуємо підстановку t = sin x, якщо n - непарне або t = cos x, якщо m - непарне.
б) Якщо m і n парні, то користуємося формулами зниження ступеня
2sin 2 x=1-cos2x, 2cos 2 x=1+cos2x.
4. Інтеграли виду

Якщо числа m і n однакової парності, використовуємо підстановку t=tg x . Часто буває зручним застосувати прийом тригонометричної одиниці.
5. ∫ sin(nx)·cos(mx)dx , ∫ cos(mx)·cos(nx)dx , ∫ sin(mx)·sin(nx)dx
Скористаємося формулами перетворення твору тригонометричних функцій на їх суму

Приклади
1. Обчислити інтеграл ∫ cos 4 x sin 3 xdx .
Робимо заміну cos(x)=t. Тоді ∫ cos 4 x·sin 3 xdx =
2. Обчислити інтеграл.
Роблячи заміну sin x = t, отримуємо

3. Знайти інтеграл.
Робимо заміну tg (x) = t. Підставляючи, отримуємо

Зауважимо, що заміна ctg(x)=t тут зручніша, тому що тоді , і тому

Інтегрування виразів виду R(sinx, cosx)

Приклад №1. Обчислити інтеграли:

Рішення.
а) Інтегрування виразів виду R(sinx, cosx) , де R - раціональна функція від sin x і cos x перетворюються в інтеграли від раціональних функцій за допомогою універсальної тригонометричної підстановки tg(x/2) = t.
Тоді маємо

Універсальна тригонометрична підстановка дає можливість перейти від інтеграла виду ∫ R(sinx, cosx) dx до інтеграла від дробово-раціональної функціїАле часто така заміна веде до громіздких виразів. При певних умовефективними виявляються простіші підстановки:

Якщо виконується рівність R(-sin x, cos x) = -R(sin x, cos x) dx, то застосовується підстановка cos x = t.
Якщо виконується рівність R(sin x, -cos x) = -R(sin x, cos x) dx, то підстановка sin x = t.
Якщо виконується рівність R(-sin x, -cos x) = R(sin x, cos x) dx, то підстановка tgx = t або ctg x = t.

У даному випадкудля знаходження інтегралу

застосуємо універсальну тригонометричну підстановку tg(x/2) = t.
Тоді
Так як дріб неправильний, то, виділяючи цілу частину, отримаємо
Повертаючись до вихідної змінної будемо мати

b) У другому прикладі розглянемо важливий окремий випадок, коли загальний вираз ∫ R(sinx, cosx) dx має вигляд ∫ sin m x·cos n xdx . У цьому випадку, якщо m непарно, слід застосувати підстановку cos x = t . Якщо непарно n, слід застосувати підстановку sin x = t. Якщо обидва показники тип - парні невід'ємні числа (зокрема, одне з них може бути рівним нулю), то виконують заміну за відомими тригонометричними формулами:
В даному випадку

Відповідь:

Інтеграл від синуса sin(x) дорівнює косинусу, причому зі знаком мінус. Багато хто часто припускається помилок тому що не може запам'ятати, що похідна від синуса дорівнює мінус косинусу, а від косинуса - синусу зі знаком плюс.
Ті, хто вивчає початкову, повинні пам'ятати, що до правої сторони слід додати постійну.
Цю постійну визначають з додаткової умови.
Графік синуса має вигляд

Синус непарна, а косинус - парна функціятому при інтегруванні з'являється знак мінус. Спочатку всім здається все простим і зрозумілим. Але рано чи пізно настає час ускладнювати інтеграл, тобто інтегрувати синус подвійного кута, потрійний аргумент і т.д. І в багатьох виникають проблеми з інтегруванням. Для виведення формули інтеграла для sin (k*x) проведемо усі викладки спочатку. Щоб звести інтеграл до табличної формули треба внести коефіцієнт під диференціал, але це змінить сам інтеграл. Тому одночасно ділимо на коефіцієнт

Знаючи цю формулу, інтеграл від синуса подвійного кута записуємо одним рядком
Далі можемо проінтегрувати синус потрійного кута
і т.д.
int(sin(k*x)=-1/k*cos(k*x).
За такою ж формулою виводять інтеграл від синуса половини кута, який дорівнює мінус 2 косинус половини кута.
Інтеграл від синуса однієї третьої х дорівнює

Поширені приклади інтегрування синусу

приклад 1. Знайти інтеграл від sin(4*x).
Рішення: За формулою інтегрування знаходимо

приклад 2. Обчислити інтеграл sin(5*x).
Рішення: Виконуємо інтегрування

приклад 3. Проінтегрувати вираз sin(7*x).

приклад 4. Знайти інтеграл функції y=sin(x/5).
Рішення: Знаходимо невизначений інтеграл

Як тільки Ви навчитеся обчислювати прості інтеграливід синуса можете переходити до певному інтегралу

Приклад 5. Знайти початкову від sin(x), яка в нулі дорівнює 2.
Рішення: Обчислюємо початкову

З умови на початкову знаходимо постійну
-cos(0)+C=2;
C = 2 + cos (0) = 3.
Повертаємося до початкової та підставляємо знайдену постійну

Це і є відповідь до завдання.

Приклад 7. Проінтегрувати синус подвійного кута y = sin (2 * x) від 0 до 45 градусів.
Рішення: Записуємо інтеграл від синуса та підставляємо межі інтегрування

За фізичним змістом певний інтеграл дорівнює площі фігури обмеженою функцією sin(x) та віссю абсцис.

Але певний інтеграл і площа, це не те саме. Інтеграл може бути негативним, а площу немає. Якщо функція велику площумає під віссю абсцис, її певний інтеграл негативний.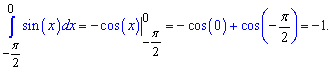

Площа криволінійної трапеціїдорівнює інтегралу від різниці рівняння верхньої кривої та нижньої.

У разі верхня крива це вісь абсцис чи y = 0. Нижня - це графік синуса. Тому формула площі синус функції дорівнює 1 або певному інтегралу по модулю.

Якщо функція антисиметрична щодо осі абсцис то її інтеграл дорівнює нулю, а площа дорівнює подвійному інтегралуграфіка над віссю абсцис. Наприклад, інтеграл синуса подвійного кута від -45 до 45 градусів дорівнює нулю.

У той же час площа заштрихованої фігури дорівнює одиниці.