Багатогранні кути теореми багатогранних кутах. Багатогранні кути багатогранний кут є просторовим аналогом багатокутника
Слайд 1
Фігура, утворена зазначеною поверхнею та однією з двох частин простору, нею обмежених, називається багатогранним кутом. Загальна вершина S називається вершиною багатогранного кута. Промені SA1, …, SAn називаються ребрами багатогранного кута, а самі плоскі кути A1SA2, A2SA3, …, An-1SAn, AnSA1 – гранями багатогранного кута. Багатогранний кут позначається літерами SA1 ... An, що вказують вершину та точки на його ребрах. Поверхня, утворена кінцевим набором плоских кутів A1SA2, A2SA3, …, An-1SAn, AnSA1 з загальною вершиною S, у яких сусідні кути не мають загальних точок, крім точок загального променя, а несусідні кути не мають загальних точокКрім загальної вершини, будемо називати багатогранною поверхнею.
Слайд 2
Залежно від кількості граней багатогранні кути бувають тригранними, чотиригранними, п'ятигранними тощо.
Слайд 3
ТРИГРАНІ КУТИ
Теорема. Кожен плоский кут тригранного кута менше сумидвох інших його плоских кутів. Розглянемо тригранний кут SABC. Нехай найбільший із його плоских кутів є кут ASC. Тоді виконуються нерівності ASB ASC
Слайд 4
Властивість. Сума плоских кутів тригранного кута менша за 360°. Аналогічно для тригранних кутів з вершинами B і С мають місце нерівності: ABС
Слайд 5
Випуклі багатогранні кути
Багатогранний кут називається опуклим, якщо він є опуклою фігурою, тобто разом з будь-якими двома своїми точками цілком містить і відрізок, що з'єднує їх. На малюнку наведені приклади опуклого і непуклого багатогранних кутів. Властивість.Сума всіх плоских кутів опуклого багатогранного кута менше 360 °. Доказ аналогічний доведенню відповідної властивості для тригранного кута.
Слайд 6
Вертикальні багатогранні кути
На рисунках наведено приклади тригранних, чотиригранних та п'ятигранних вертикальних кутів Теорема. Вертикальні кутирівні.
Слайд 7
Вимірювання багатогранних кутів
Оскільки градусна величина розгорнутого двогранного кута вимірюється градусною величиною відповідного лінійного кута і дорівнює 180о, то вважатимемо, що градусна величина всього простору, що складається з двох розгорнутих двогранних кутів, дорівнює 360о. Розмір багатогранного кута, виражена в градусах, показує яку частину простору займає даний багатокутний кут. Наприклад, тригранний кут куба займає одну восьму частину простору і, отже, його градусна величина дорівнює 360о: 8 = 45о. Тригранний кут у правильній n-вугільної призмидорівнює половині двогранного кута при бічному ребрі. Враховуючи, що цей двогранний кут дорівнює, отримуємо, що тригранний кут призми дорівнює.
Слайд 8
Вимірювання трикутних кутів*
Виведемо формулу, що виражає величину тригранного кута через його двогранні кути. Опишемо біля вершини Sтрехгранного кута одиничну сферу і позначимо точки перетину ребер тригранного кута з цією сферою A, B, C. Площини граней тригранного кута розбивають цю сферу на шість попарно рівних сферичних двокутників, що відповідають двогранним кутам даного тригранного. Сферичний трикутник ABC і симетричний йому сферичний трикутник A"B"C" є перетином трьох двокутників.
Слайд 9
Вимірювання багатогранних кутів*
Нехай SA1 ... An - опуклий n-гранний кут. Розбиваючи його на тригранні кути, проведенням діагоналей A1A3, …, A1An-1 та застосовуючи до них отриману формулу, матимемо: SA1 + … + SAn = 180о(n – 2) + 2SA1…An. Багатогранні кутиможна вимірювати і числами. Дійсно, трьомстам шістдесяти градусів всього простору відповідає число 2? Переходячи від градусів до числа в отриманій формулі, матимемо: SA1+ …+SAn = π(n – 2) + 2SA1…An.
Слайд 10
Вправа 1
Чи може бути тригранний кут із плоскими кутами: а) 30°, 60°, 20°; б) 45 °, 45 °, 90 °; в) 30 °, 45 °, 60 °? Відповіді немає; б) ні; в) так.
Слайд 11
Вправа 2
Наведіть приклади багатогранників, у яких грані, перетинаючи у вершинах, утворюють лише: а) тригранні кути; б) чотиригранні кути; в) п'ятигранні кути. Відповідь: а) Тетраедр, куб, додекаедр; б) октаедр; в) ікосаедр.
Слайд 12
Вправа 3
Два плоскі кути тригранного кута дорівнюють 70° і 80°. У яких межах знаходиться третій плоский кут? Відповідь: 10о
Слайд 13
Вправа 4
Плоскі кути тригранного кута дорівнюють 45 °, 45 ° і 60 °. Знайдіть величину кута між площинами плоских кутів 45°. Відповідь: 90о.
Слайд 14
Вправа 5
У тригранному куті два плоскі кути рівні по 45°; двогранний кут між ними прямий. Знайдіть третій плоский кут. Відповідь: 60о.
Слайд 15
Вправа 6
Плоскі кути тригранного кута дорівнюють 60°, 60° та 90°. На його ребрах від вершини відкладено рівні відрізки OA, OB, OC. Знайдіть двогранний кут між площиною кута 90° і площиною ABC. Відповідь: 90о.
Слайд 16
Вправа 7
Кожен плоский кут тригранного кута дорівнює 60 °. На одному з його ребер відкладений від вершини відрізок, що дорівнює 3 см, і з кінця опущений перпендикуляр на протилежну грань. Знайдіть довжину цього перпендикуляра. Відповідь: див.
Слайд 17
Вправа 8
Знайдіть геометричне місце внутрішніх точоктригранного кута, рівновіддаленого від його граней. Відповідь: Промінь, вершиною якого є вершина тригранного кута, що лежить на лінії перетину площин, що ділять двогранні кути навпіл.
Слайд 18
Вправа 9
Знайдіть геометричне місце внутрішніх точок тригранного кута, рівновіддалених від його ребер. Відповідь: Промінь, вершиною якого є вершина тригранного кута, що лежить на лінії перетину площин, що проходять через бісектриси плоских кутів і перпендикулярних площин цих кутів.
Слайд 19
Вправа 10
Для двогранних кутів тетраедра маємо: , звідки 70о30". Для тригранних кутів тетраедра маємо: 15о45". Відповідь: 15о45". Знайдіть наближені значення тригранних кутів тетраедра.
Слайд 20
Вправа 11
Знайдіть наближені значення чотиригранних кутів октаедра. Для двогранних кутів октаедра маємо: , звідки 109о30". Для чотиригранних кутів октаедра маємо: 38о56". Відповідь: 38о56".
Слайд 21
Вправа 12
Знайдіть наближені значення п'ятигранних кутів ікосаедра. Для двогранних кутів ікосаедра маємо: , звідки 138о11". Для п'ятигранних кутів ікосаедра маємо: 75о28". Відповідь: 75о28".
Слайд 22
Вправа 13
Для двогранних кутів додекаедра маємо: , звідки 116о34". Для тригранних кутів додекаедра маємо: 84о51". Відповідь: 84о51". Знайдіть наближені значення тригранних кутів додекаедра.
Слайд 23
Вправа 14
У правильній чотирикутній піраміді SABCD сторона основи дорівнює 2 см, висота 1 см. Знайдіть чотиригранний кут при вершині цієї піраміди. Рішення: Зазначені піраміди розбивають куб на шість рівних пірамід з вершинами в центрі куба. Отже, 4-х гранний кут при вершині піраміди становить одну шосту частину кута 360о, тобто. дорівнює 60о. Відповідь: 60о.
Слайд 24
Вправа 15
У правильній трикутної піраміди бічні ребрадорівнюють 1, кути при вершині 90о. Знайдіть тригранний кут при вершині цієї піраміди. Рішення: Вказані піраміди розбивають октаедр на вісім рівних пірамід з вершинами в центрі O октаедра. Отже, 3-х гранний кут при вершині піраміди становить одну восьму частину кута 360о, тобто. дорівнює 45о. Відповідь: 45о.
Слайд 25
Вправа 16
У правильній трикутній піраміді бічні ребра дорівнюють 1, а висота Знайдіть тригранний кут при вершині цієї піраміди. Рішення: Вказані піраміди розбивають правильний тетраедрна чотири рівні пірамідиз вершинами в центрі Oтетраедра. Отже, 3-гранний кут при вершині піраміди становить одну четверту частину кута 360о, тобто. дорівнює 90о. Відповідь: 90о.
Переглянути всі слайди
Багатогранні кути Багатогранний кут є просторовим аналогомбагатокутник на площині. Нагадаємо, що багатокутником на площині називається фігура, утворена простою замкненою ламаною цієї площини та обмеженою нею внутрішньою областю.
Визначення багатогранного кута Поверхня, утворену кінцевим набором плоских кутів A1SA2, A2SA3, …, An-1SAn, An. SA 1 із загальною вершиною S, в яких сусідні кути не мають загальних точок, крім точок загального променя, а не сусідні кути не мають спільних точок, крім загальної вершини, називатимемо багатогранною поверхнею. Фігура, утворена зазначеною поверхнею та однією з двох частин простору, нею обмежених, називається багатогранним кутом. Загальна вершина S називається вершиною багатогранного кута. Промені SA 1, …, SAn називаються ребрами багатогранного кута, а самі плоскі кути A 1 SA 2, A 2 SA 3 …, An-1 SAn, An. SA 1 – гранями багатогранного кута. Багатогранний кут позначається літерами SA 1 ... An, що вказують вершину та точки на його ребрах.
Види багатогранних кутів Залежно від кількості граней багатогранні кути бувають тригранними, чотиригранними, п'ятигранними тощо.
Вправа 1 Наведіть приклади багатогранників, у яких грані, що перетинаються у вершинах, утворюють лише: а) тригранні кути; б) чотиригранні кути; в) п'ятигранні кути. Відповідь: а) Тетраедр, куб, додекаедр; б) октаедр; в) ікосаедр.
Вправа 2 Наведіть приклади багатогранників, у яких грані, перетинаючись у вершинах, утворюють лише: а) тригранні та чотиригранні кути; б) тригранні та п'ятигранні кути; в) чотиригранні та п'ятигранні кути. Відповідь: а) чотирикутна пірамідатрикутна біпіраміда; б) п'ятикутна піраміда; в) п'ятикутна біпіраміда.
Нерівність трикутника Для трикутника має місце така теорема. Теорема (Нерівність трикутника). Кожна сторона трикутника менша від суми двох інших сторін. Доведемо, що з тригранного кута має місце наступний просторовий аналог цієї теореми. Теорема. Кожен плоский кут тригранного кута менший за суму двох інших його плоских кутів.
Розглянемо тригранний кут SABC. Нехай найбільший із його плоских кутів є кут ASC. Тоді виконуються нерівності ASB ASC
Точка перетину бісектрис Для трикутника має місце така теорема. Теорема. Бісектриси трикутника перетинаються в одній точці – центрі вписаного кола. Доведемо, що з тригранного кута має місце наступний просторовий аналог цієї теореми. Теорема. Біссектральні площини двогранних кутів тригранного кута перетинаються однією прямою.
Розглянемо тригранний кут SABC. Біссектральна площина двостороннього SAD кута SA є геометричним місцем точок цього кута, рівновіддалених від його граней SAB і SAC. Аналогічно, біссектральна площина SBE двогранного кута SB є геометричним місцем точок цього кута, віддалених від його граней SAB і SBC. Лінія їх перетину SO складатиметься з точок, що рівно віддалені від усіх граней тригранного кута. Отже, через неї проходитиме біссектральна площина двогранного кута SC.
Крапка перетину серединних перпендикулярів Для трикутника має місце така теорема. Теорема. Серединні перпендикуляридо сторін трикутника перетинаються в одній точці – центр описаного кола. Доведемо, що з тригранного кута має місце наступний просторовий аналог цієї теореми. Теорема. Площини, що проходять через бісектриси граней тригранного кута і перпендикулярні до цих граней, перетинаються по одній прямій.
Розглянемо тригранний кут SABC. Площина, що проходить через бісектрису SD кута BSC і перпендикулярна до його площини, складається з точок рівновіддалених від ребер SB і SC тригранного кута SABC. Аналогічно, площина, що проходить через бісектрису SE кута ASC і перпендикулярна до його площини, складається з точок рівновіддалених від ребер SA і SC тригранного кута SABC. Лінія їх перетину SO складатиметься з точок, що рівно віддалені від усіх ребер тригранного кута. Отже, її міститиме площину, що проходить через бісектрису кута ASB і перпендикулярна його площині.
Точка перетину медіан Для трикутника має місце така теорема. Теорема. Медіани трикутника перетинаються в одній точці – центрі вписаного кола. Доведемо, що з тригранного кута має місце наступний просторовий аналог цієї теореми. Теорема. Площини, що проходять через ребра тригранного кута та бісектриси протилежних граней, перетинаються по одній прямій.
Розглянемо тригранний кут SABC. На його ребрах відкладемо рівні відрізки SA = SB = CS. Бісектриси SD, SE, SF плоских кутів тригранного кута є медіанами трикутників відповідно SBC, SAB. Отже, AD, BE, CF – медіани трикутника ABC. Нехай O – точка перетину медіан. Тоді пряма SO буде лінією перетину площин, що розглядаються.
Точка перетину висот Для трикутника має місце така теорема. Теорема. Висоти трикутника або їх продовження перетинаються в одній точці. Доведемо, що з тригранного кута має місце наступний просторовий аналог цієї теореми. Теорема. Площини, що проходять через ребра тригранного кута і перпендикулярні до площин протилежних граней, перетинаються по одній прямій.
Розглянемо тригранний кут Sabc. Нехай d, e, f – лінії перетину площин граней тригранного кута з площинами, що проходять через ребра a, b, c цього кута і перпендикулярні до відповідних площин граней. Виберемо якусь точку C на ребрі с. Опустимо з неї перпендикуляри CD та CE на прямі d та e відповідно. Позначимо A та B точки перетину прямих CD та CE з прямими SB та SA відповідно. Пряма d є ортогональною проекцієюпряма AD на площину BSC. Так як BC перпендикулярна до прямої d, то вона перпендикулярна і до прямої AD. Аналогічно, пряма AC перпендикулярна до прямої BE. Нехай O – точка перетину прямих AD та BE. Пряма BC перпендикулярна площині SAD, отже, вона перпендикулярна до прямої SO. Аналогічно, Пряма AC перпендикулярна площині SBE, отже, вона перпендикулярна до прямої SO. Таким чином, пряма SO перпендикулярна прямим BC і AC, отже перпендикулярна площині ABC, значить, перпендикулярна і прямий AB. З іншого боку, пряма CO перпендикулярна до прямої AB. Таким чином, пряма AB перпендикулярна до площини SOC. Площина SAB проходить через пряму AB, перпендикулярну площині SOC, отже, сама перпендикулярна цій площині. Отже, всі три площини, що розглядаються, перетинаються по прямій SO.
Сума плоских кутів Теорема. Сума плоских кутів тригранного кута менша за 360°. Доведення. Нехай SABC – це трикутний кут. Розглянемо тригранний кут із вершиною A, утворений гранями ABS, ACS та кутом BAC. Через нерівність трикутника, має місце нерівність BAС
Випуклі багатогранні кути Багатогранний кут називається опуклим, якщо він є опуклою фігурою, тобто разом з будь-якими двома своїми точками цілком містить і відрізок, що з'єднує їх. На малюнку наведено приклади опуклого та невипуклого багатогранних кутів. Властивість. Сума всіх плоских кутів опуклого багатогранного кута менша за 360°. Доказ аналогічний доведенню відповідної властивості для тригранного кута. 
Вправа 5 Два плоскі кути тригранного кута дорівнюють 70° та 80°. У яких межах знаходиться третій плоский кут? Відповідь: 10 про
Вправа 6 Плоскі кути тригранного кута дорівнюють 45°, 45° та 60°. Знайдіть величину кута між площинами плоских кутів 45°. Відповідь: 90 о.
Вправа 7 У тригранному куті два плоскі кути рівні по 45°; двогранний кут між ними прямий. Знайдіть третій плоский кут. Відповідь: 60 о.
Вправа 8 Плоскі кути тригранного кута дорівнюють 60°, 60° та 90°. На його ребрах від вершини відкладено рівні відрізки OA, OB, OC. Знайдіть двогранний кут між площиною кута 90° і площиною ABC. Відповідь: 90 о.
Вправа 9 Кожен плоский кут трикутного кута дорівнює 60°. На одному з його ребер відкладений від вершини відрізок, що дорівнює 3 см, і з кінця опущений перпендикуляр на протилежну грань. Знайдіть довжину цього перпендикуляра. Відповідь: див.
БАГАТОГРАНІ КУТИ
Багатогранний кут є просторовим аналогом багатокутника. Нагадаємо, що багатокутником на площині називається фігура, утворена простою замкненою ламаною та обмеженою нею внутрішньою областю. Вважатимемо аналогом точки на площині промінь у просторі та аналогом відрізка на площині плоский кут у просторі. Тоді аналогом простої замкнутої ламаної на площині є поверхня, утворена кінцевим набором плоских кутів.A 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 із загальною вершиноюS (рис. 1), у яких сусідні кути немає спільних точок, крім точок загального променя, а несусідні кути немає спільних точок, крім загальної вершини. Фігура, утворена зазначеною поверхнею та однією з двох частин простору, нею обмежених, називається багатогранним кутом. Загальна вершинаSназивається вершиноюбагатогранного кута. ПроменіSA 1 , …, SA nназиваються ребрамибагатогранного кута, а самі плоскі кутиA 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 – гранямибагатогранного кута. Багатогранний кут позначається літерамиSA 1 … A n, що вказують вершину та крапки на його ребрах. Залежно від числа граней багатогранні кути називаються тригранними, чотиригранними, п'ятигранними (рис. 2) тощо.
Багатогранний кут називається опуклим, якщо він є опуклою фігурою, тобто. разом з будь-якими двома своїми точками містить і з'єднує їхвідрізок. На малюнку 2 тригранний та чотиригранний кути опуклі, а п'ятигранний кут – ні.
Розглянемо деякі властивості трикутників та аналогічні їм властивості тригранних кутів.
Властивість 1(Нерівність трикутника). Кожна сторона трикутника менша за суму двох інших його сторін.
Аналогічним властивістю для тригранних кутів є така властивість.
Властивість 1Кожен плоский кут тригранного кута менший за суму двох інших його плоских кутів.
Доведення.
Розглянемо тригранний кут SABC
.
Нехай найбільший із його плоских кутів є кут ASC. Тоді виконуються нерівності
ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .
Таким чином, залишається довести нерівність AСС< ASB+ BSC.
Відкладемо на межі ASCкут ASD, рівний ASB
,
і точку Bвиберемо так, щоб SB = SD(Рис. 3). Тоді трикутники ASBі ASDрівні (по обидва боки і кут між ними) і, отже, AB = AD. Скористаємося нерівністю трикутника AC< AB + BC
. Віднімаючи з обох його частин AD = AB, отримаємо нерівність DC< BC.
У трикутниках DSCі BSCодна сторона загальна ( SC), SD = SBі DC< BC.
В цьому випадку проти більшої сторони лежить більший куті, отже, DSC< BSC
. Додаючи до обох частин цієї нерівності кут ASD
,
рівний ASB, отримаємо потрібну нерівність AСС< ASB+ BSC.
Наслідок 1.Сума плоских кутів тригранного кута менше 360°
.
Доведення.
Нехай SABC- Цей трикутний кут. Розглянемо тригранний кут із вершиною A, утворений гранями ABS, ACSта кутом BAC. З огляду на доведену властивість, має місце нерівність BАС< BAS+ CAS. Аналогічно для трикутних кутів з вершинами. Bі Змають місце нерівності: ABС< ABS+ CBS, ACB< ACS+ BCS. Складаючи ці нерівності та враховуючи, що сума кутів трикутника ABCдорівнює 180° , отримуємо 180 ° < BAS +CAS+ ABS + CBS + BCS+ ACS = 180
°
- ASB + 180° - BSC+ 180° - ASC. Отже, ASB + BSC + ASC<
360
°
.
Наслідок 2.Сума плоских кутів опуклого багатогранного кута менша за 360.
Доказ аналогічний попередньому.
Наслідок 3.Сума двогранних кутів тригранного кута більше 180°
.
Доведення.
Нехай SABC- Тригранний кут. Виберемо якусь точку Pусередині нього і опустимо з неї перпендикуляри PA
1 ,
PB 1 ,
PC 1 на межі (рис. 4).
Плоскі кути B
1 PC 1 ,
A 1 PC 1 ,
A 1 PB 1 доповнюють відповідні двогранні кути з ребрами SA, SB, SCдо 180°
. Отже, сума цих двогранних кутів дорівнює 540°
- ( B
1 PC 1 +A 1 PC 1 + A
1 PB 1 ). Враховуючи, що сума плоских трикутних кутів з вершиною Pкута менше 360°
, Отримуємо, що сума двогранних кутів вихідного тригранного кута більше 180°
.
Властивість 2.Бісектриси трикутника перетинаються в одній точці.
Властивість 2".Біссектральні площини двогранних кутів тригранного кута перетинаються однією прямою.
Доказ аналогічний плоскому випадку. А саме, нехай SABC- Тригранний кут. Біссектральна площина двогранного кута SAє ГМТ кута, рівновіддалених від його граней ASCі ASB. Аналогічно, біссектральна площина двогранного кута. SBє ГМТ кута, рівновіддалених від його граней BSAі BSC
.
Лінія їхнього перетину SOбуде рівновіддалена від усіх граней тригранного кута і, отже, через неї проходитиме біссектральна площина двогранного кута. SC
.
Властивість 3.Серединні перпендикуляри до сторін трикутника перетинаються лише у точці.
Властивість 3".Площини, що проходять через бісектриси граней тригранного кута і перпендикулярні до цих граней, перетинаються по одній прямій.
Доказ аналогічний доведенню попередньої якості.
Властивість 4.Медіани трикутника перетинаються в одній точці.
Властивість 4".Площини, що проходять через ребра тригранного кута та бісектриси протилежних граней перетинаються по одній прямій.
Доведення.
Розглянемо тригранний кут SABC, SA = SB = SC(Рис. 5). Тоді бісектриси SA
1 ,
SB 1 ,
SC 1 кутів BSC, ASC, ASB
є медіанами відповідних трикутників. Тому AA
1 ,
BB 1 ,
CC 1 – медіани трикутника ABC. Нехай O- Точка їх перетину. Пряма SOміститься у всіх трьох площинах, що розглядаються, і, отже, є лінією їх перетину.
Властивість 5.Висоти трикутника перетинаються в одній точці.
Властивість 5Площини, що проходять через ребра тригранного кута і перпендикулярні протилежним граням, перетинаються по одній прямій.
Доведення.
Розглянемо тригранний кут із вершиною Sта ребрами a, b, c.Позначимо a
1 ,
b 1 ,
c 1 – лінії перетину граней з площинами, що проходять через відповідні ребра та перпендикулярні до цих граней (рис. 6). Зафіксуємо точку Cна ребрі cі опустимо з неї перпендикуляри CA
1
і CB 1 на прямі a 1 та b
1 .
Позначимо Aі Bперетину прямих CA
1 та CB
1 з прямими aі b. Тоді SA
1
є проекцією AA
1
на межу BSC. Так як BCперпендикулярна SA
1 , то вона перпендикулярна і AA
1 .
Аналогічно, ACперпендикулярна BB
1 . Таким чином, AA
1 та BB
1
є висотами трикутника ABC. Нехай O- Точка їх перетину. Площини, що проходять через прямі aі a
1 ,
bі b
1
перпендикулярні до площини ABCі, отже, лінія їхнього перетину SOперпендикулярна ABC. Значить, SOперпендикулярна AB. З іншого боку, COперпендикулярна AB. Тому площина, що проходить через ребро cі SOбуде перпендикулярна до протилежної грані.
Властивість 6 (теорема синусів).
У трикутнику ABCзі сторонами a, b, cвідповідно, мають місце рівності a
: sin A = b: sin B = c: sin C.
Властивість 6".Нехай a, b, g - Плоскі кути тригранного кута, a, b, c- Протилежні їм двогранні кути. Тоді sin a : sin a= sin b : sin b= sin g : sin c.
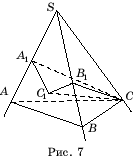
Доведення.Нехай SABC- Тригранний кут. Опустимо з точки Cперпендикуляр CC
1
на площину ASBта перпендикуляр CA
1
на ребро SA(Мал. 7). Тоді кут CA
1 C 1 буде лінійним кутомдвогранного кута a. Тому CC
1
=
CA 1 sin a
=
SC sin b sin a.
Аналогічно показується, що CC
1
= CB 1 sin b = SC sin
a sin b.
Отже, має місце рівність sin b sin a = sin a sin bі, отже, рівність sin a: sin a= sin b : sin b. Аналогічним чином доводиться, що має місце рівність sin b : sin b= sin g : sin c.
Властивість 7.Якщо в опуклий чотирикутникможна вписати коло, то суми протилежних сторін рівні.
Властивість 7".Якщо опуклий чотиригранний кут можна вписати сферу, то суми протилежних плоских кутів рівні.
Література
1. Адамар Ж. Елементарна геометрія. Частина ІІ. Стереометрія. - М.: Учпедгіз, 1938.
2. Перепілкін Д.І. Курс елементарної геометрії Частина ІІ. Геометрія у просторі. - М.-Л.: Гостехіздат, 1949.
3. Енциклопедія елементарної математики. Книга IV. Геометрія. - М.; 1963.
4. Смирнова І.М. У світі багатогранників. - М.: Просвітництво, 1995.
ТЕКСТОВЕ РОЗШИФРУВАННЯ УРОКУ:
У планіметрії одним із об'єктів вивчення є кут.
Кут - це геометрична фігура, Що складається з точки - вершини кута та двох променів, що виходять з цієї точки.
Два кути одна сторона, яких загальна та дві інші є продовженням одна одної, у планіметрії називаються суміжними.
Циркуль можна як модель плоского кута.
Згадаймо поняття двогранного кута.
Це фігура, утворена прямою а і двома напівплощинами з спільним кордонома, які не належать одній площині в геометрії називається двогранним кутом. Напівплощини – це грані двогранного кута. Пряма а – це ребро двогранного кута.
Дах будинку демонструє двогранний кут.
Але дах будинку на малюнку два виконаний у вигляді фігури утвореної з шести плоских кутів із загальною вершиною так, що кути беруться в певному порядкуі кожна пара сусідніх кутів, включаючи перший та останній, має спільну сторону. Як називається така форма даху?
У геометрії фігура, складена з кутів
А кути з яких складено цей кут називають плоскими кутами. Сторони плоских кутів називаються ребрами багатокутного кута. Точка О називається вершиною кута.
Приклади багатогранних кутів можна знайти в тетраедрі та паралелепіпеді.
Грані тетраедра DBA, ABC, DBC утворюють багатогранний кут ВADC. Найчастіше він називається тригранним кутом.
У паралелепіпеді грані АА1D1D, ABCD, AA1B1B утворюю тригранний кут AA1DB.
Ну а дах будинку виконаний у формі шестигранного кута. Вона складається із шести плоских кутів.
Для багатогранного кута справедливий ряд властивостей. Сформулюємо їх та доведемо. Тут сказано, що твердження
По-перше, для будь-якого опуклого багатогранного кута існує площина, що перетинає всі його ребра.
Розглянь докази багатогранний кут ОА1А2 А3…Аn.
За умовою він опуклий. Кут називається опуклим, якщо він лежить по одну сторону від площини кожного зі своїх плоских кутів.
Так як за умовою цей кут опуклий, то точки О, А1, А2, А3, Аn лежать по одну сторону від площини ОА1А2
Проведемо середню лінію KM трикутника ОА1А2 і виберемо з ребер ОА3, ОА4, ОАn те ребро, що утворює з площиною ГКМ, найменший двогранний кут. Нехай це буде ребро ОАi.
Розглянемо напівплощину α з кордоном КМ, що поділяє двогранний кут ОКМАi на два двогранні кути. Усі вершини від А до Аn лежать з одного боку від площині α, а точка О з іншого боку. Отже, площина перетинає всі ребра багатогранного кута. Твердження доведене.
Випуклі багатогранні кути мають ще одну важливу властивість.
Сума плоских кутів опуклого багатогранного кута менша за 360°.
Розглянемо опуклий багатогранний кут з вершиною в точці О. У силу доведеного твердження існує площина, яка перетинає його ребра.
Проведемо таку площину, нехай вона перетинає ребра кута в точках А1, А2, А3 і так далі Аn.
Площина від зовнішньої областіплоского кута відсікатиме трикутник. Сума кутів якого 180 °. Отримаємо, що сума всіх плоских кутів від А1ОА2 до АnОА1 дорівнює виразу перетворимо, цей вираз перегрупуємо складові, отримаємо
У даному виразі суми зазначені в дужках є сумами плоских кутів тригранного кута, а як відомо вони більше третього плоского кута.
Цю нерівність можна записати для всіх тригранних кутів, що утворюють даний багатогранний кут.
Отже, отримаємо наступне продовженнярівності
Отримана відповідь доводить, що сума плоских кутів опуклого багатогранного кута менша за 360 градусів.
МАОУ «Ліцей інноваційних технологій»
Багатогранні кути. Випуклі багатогранники
Підготував учень 10Б класу: Бурикін Олексій
Перевірив: Дубінська І.А.
Хабаровськ
Багатогранний кут
Багатогранним кутомназивається фігура, утворена плоскими кутами так, що виконуються умови:
1) ніякі два кути не мають спільних точок, крім їх загальної вершини або цілої сторони;
2) у кожного з цих кутів кожна його сторона є спільною з одним і лише одним іншим таким кутом;
3) від кожного кута до кожного можна перейти кутами, що мають спільну сторону;
4) ніякі два кути з спільною стороноюне лежать у одній площині.
- Кути ASB, BSC,... називаються плоскими кутамиабо гранями, сторони їх SA, SB, ... називаються ребрами, а загальна вершина S- вершиноюбагатогранного кута.
Теорема1.
У тригранному куті кожен плоский кут менший за суму двох інших плоских кутів.
Слідство
- / ASC - / ASB/CSB; / ASC - / CSB/ASB.
У тригранному куті кожен плоский кут більший за різницю двох інших кутів. .
Теорема2.
- Сума величин усіх трьох плоских кутів тригранного кута менша за 360° .
180°, звідки і слідує, що α + β + γ " width = "640" Доведення
Позначимо,
тоді з трикутників ASC, ASB, BSC маємо
Тепер нерівність набуває вигляду
180 ° - α + 180 ° - β + 180 ° - γ 180 °,
звідки й випливає, що
α + β + γ
Найпростіші випадки рівності тригранних кутів
- 1) по рівному двогранному кутку, укладеному між двома відповідно рівними і однаково розташованими плоскими кутами , або 2) по рівному плоскому кутку, укладеному між двома відповідно рівними і однаково розташованими двогранними кутами .
Випуклий багатогранний кут
- Багатогранний кут називається опуклим, якщо він весь розташований по одну сторону від площини кожної його граней, необмежено продовженої.
Багатогранник.
Багатогранник, у тривимірному просторі- сукупність кінцевого числаплоских багатокутників, така, що кожна сторона будь-якого багатокутника є одночасно сторона іншого, званого суміжним з першим.
Випуклі багатогранники
Багатогранникназивається опуклимякщо він весь лежить по одну сторону від площини будь-якої його грані; тоді грані його теж опуклі.
Випуклий багатогранникрозрізає простір на дві частини – зовнішню та внутрішню. Внутрішня частина є опукле тіло. Назад, якщо поверхня опуклого тіла багатогранна, то відповідний багатогранник – опуклий.
Теорема.Сума всіх плоских кутів опуклого багатогранного кута менша за 360 градусів.
Властивість 1.У опуклому багатограннику усі грані є опуклими багатокутниками.
Властивість2.Будь-який опуклий багатогранник може бути складений із пірамід із загальною вершиною, основа яких утворює поверхню багатогранника.
