Рівняння шредінгера у викривленому просторі. Рівняння шредінгера для стаціонарних станів
Зробимо малюнокУ нашій задачі функція U(x) має особливий, розривний вигляд: вона дорівнює нулю між стінками, а на краях ями (на стінках) звертається до нескінченності:
![]()
Запишемо рівняння Шредінгера для стаціонарних станів частинок у точках розташованих між стінками:
або, якщо врахувати формулу (1.1)
![]()
До рівняння (1.3) необхідно додати граничні умови на стінках ями. Візьмемо до уваги, що хвильова функціяпов'язана з ймовірністю знаходження частинок. Крім того, за умовами завдання за межами стінок частка не може бути виявлена. Тоді хвильова функція на стінках і за їх межами повинна звертатися в нуль, і граничні умови завдання набувають простого вигляду:
Тепер приступимо до вирішення рівняння (1.3). Зокрема можна врахувати, що його рішенням є хвилі де-Бройля. Але одна хвиля де-Бройля як рішення, до нашого завдання явно не відноситься, оскільки вона свідомо описує вільну частинку, що «біжить» в одному напрямку. А в нас частка бігає «туди-сюди» між стінками. У такому разі на підставі принципу суперпозиції шукане рішення можна спробувати подати у вигляді двох хвиль де-Бройля, що біжать один одному назустріч з імпульсами p і -p, тобто у вигляді:
Постійні і можна знайти з однієї з граничних умов та умов нормування. Останнє говорить про те, що якщо скласти всі ймовірності, тобто знайти ймовірність виявлення електрона між стінками взагалі в (будь-якому місці), то вийде одиниця (ймовірність достовірної події дорівнює 1), тобто:
![]()
Згідно з першою граничною умовою маємо:
Таким чином, отримаємо розв'язання нашого завдання:
Як відомо, . Тому знайдене рішення можна переписати у вигляді:
Постійна А визначається за умови нормування. Але тут не вона репрезентує особливий інтерес. Залишилася невикористаною друга гранична умова. Який результат воно дає змогу отримати? Щодо знайденого рішення (1.5) воно призводить до рівняння:
З нього бачимо, що в нашому завданні імпульс p може приймати не будь-які значення, а лише значення
До речі, n неспроможна дорівнювати нулю, оскільки хвильова функція тоді всюди на проміжку (0…l) дорівнювала нулю! Це означає, що частка між стінами не може бути в спокої! Вона обов'язково має рухатися. В аналогічних умовах знаходяться електрони провідності металу. Отриманий висновок поширюється і них: електрони в металі неможливо знайти нерухомими.
Найменший можливий імпульс електрона, що рухається, дорівнює
![]()
Ми вказали, що імпульс електрона при відображенні стін змінює знак. Тому на питання, який імпульс у електрона, коли він замкнений між стінками, безперечно відповісти не можна: чи то +p, чи то -p. Імпульс невизначений. Його ступінь невизначеності, зрозуміло, визначається так: =p-(-p)=2p. Невизначеність координати дорівнює l; якщо спробувати «зловити» електрон, то його буде виявлено в межах між стінками, але де точно — невідомо. Оскільки найменше значення p дорівнює , отримуємо:
Ми підтвердили співвідношення Гейзенберга за умов нашого завдання, тобто за умови існування найменшого значення p. Якщо ж пам'ятати довільно-можливе значення імпульсу, то співвідношення невизначеності отримує такий вид:
Це означає, що вихідний постулат Гейзенберга-Боpа про невизначеність і встановлює лише нижній кордонневизначеностей, можливу при вимірах. Якщо початку руху система була наділена мінімальними невизначеностями, то з часом вони можуть зростати.
Однак формула (1.6) вказує і на інший надзвичайно цікавий висновок: виявляється, імпульс системи в квантовій механіці не завжди може змінюватися безперервно (як це завжди має місце в класичної механіки). Спектр імпульсу частинки в прикладі дискретний, імпульс частинки між стінками може змінюватися тільки стрибками (квантами). Величина стрибка в розглянутій задачі постійна і рівна.
На рис. 2. наочно зображений діапазон можливих значень імпульсу частки. Таким чином, дискретність зміни механічних величин, зовсім далека від класичної механіки, у квантовій механіці випливає з її математичного апарату. На питання, чому імпульс змінюється стрибками, наочного знайти не можна. Такі закони квантової механіки; наш висновок випливає з них логічно – у цьому все пояснення.

Звернемося тепер до енергії частки. Енергія пов'язана з імпульсом формулою (1). Якщо спектр імпульсу дискретний, автоматично виходить, як і спектр значень енергії частки між стінками дискретний. І він знаходиться просто. Якщо можливі значення згідно з формулою (1.6) підставити у формулу (1.1), отримаємо:
![]()
де n = 1, 2, ..., і називається квантовим числом.
Таким чином ми отримали енергетичні рівні.

Мал. 3 зображує розташування енергетичних рівнів, що відповідає умовам нашого завдання. Зрозуміло, що з іншого завдання розташування енергетичних рівнів буде іншим. Якщо частка є зарядженою (наприклад, це електрон), то, перебуваючи не на нижчому енергетичному рівні, вона зможе спонтанно випромінювати світло (у вигляді фотона). При цьому вона перейде на нижчу енергетичний рівеньвідповідно до умови:
Хвильові функції для кожного стаціонарного стану в нашому завданні є синусоїдами, нульові значення яких обов'язково потрапляють на стінки. Дві такі хвильові функції n = 1,2 зображені на рис. 1.
Вид хвильового рівняння фізичної системивизначається її гамільтоніаном, який набуває в силу цього фундаментальне значенняу всьому математичний апаратквантової механіки
Вид гамільтоніана вільної частки встановлюється вже загальними вимогами, пов'язаними з однорідністю та ізотропією простору та принципом відносності Галілея. У класичній механіці ці вимоги призводять до квадратичної залежності енергії частки від її імпульсу: де стала називається масою частинки (див. I, § 4). У квантовій механіці самі вимоги призводять до такому ж співвідношенню для власних значень енергії та імпульсу - одночасно вимірних збережених (для вільної частки) величин.
Але для того щоб співвідношення мало місце для всіх власних значень енергії та імпульсу, воно має бути справедливим і для їхніх операторів:
![]()
Підставивши сюди (15,2), отримаємо гамільтоніан вільно рухомої частки у вигляді
![]()
де – оператор Лапласа.
Гамільтоніан системи невзаємодіючих частинок дорівнює сумігамільтоніанів кожної з них:
![]()
де індекс нумерує частинки; - оператор Лапласа, у якому диференціювання провадиться за координатами частки.
У класичній (нерелятивістській) механіці взаємодія частинок описується адитивним членом у функції Гамільтона - потенційною енергією взаємодії функцією координат частинок.
Додаванням такої ж функції до гамільтоніану системи описується і взаємодія частинок квантової механіки:
![]()
перший член можна як оператор кінетичної енергії, а другий – як оператор потенційної енергії. Зокрема, гамільтоніан для однієї частки, що знаходиться у зовнішньому полі,
де U(х, у, z) - потенціальна енергіячастинки у зовнішньому полі.
Підстановка виразів (17,2)-(17,5) загальне рівняння(8,1) дає хвильові рівняння відповідних систем. Випишемо тут хвильове рівняння для частки у зовнішньому полі
Рівняння ж (10,2), що визначає стаціонарні стани, набуває вигляду
Рівняння (17,6), (17,7) були встановлені Шредінгером в 1926 і називаються рівняннями Шредінгера.
Для вільної частки рівняння (17,7) має вигляд
![]()
Це рівняння має кінцеві у всьому просторі рішення за будь-якого позитивне значенняенергії Е. Для станів з певними напрямками руху цими рішеннями є власні функціїоператора імпульсу, причому . Повні (залежні від часу) хвильові функції таких стаціонарних станів мають вигляд
![]() (17,9)
(17,9)
Кожна така функція - плоска хвиля - описує стан, в якому частка володіє певними енергією Е та імпульсом. Частота цієї хвилі дорівнює, а її хвильовий вектор відповідну довжину хвилі називають дебройлівською довжиною хвилі частинки.
Енергетичний спектр вільно рухомої частки виявляється, таким чином, безперервним, простягаючись від нуля до Кожне з цих власних значень (за винятком тільки значення вироджене, причому виродження - нескінченної кратності. Дійсно, кожному відмінному від нуля значення Е відповідає безлічвласних функцій (17,9), що відрізняються напрямками вектора за однакової його абсолютної величини.
Простежимо, як відбувається у рівнянні Шредінгера граничний перехіддо класичної механіки, розглядаючи для простоти лише одну частинку у зовнішньому полі. Підставивши в рівняння Шредінгера (17,6) граничний вираз (6,1) хвильової функції отримаємо, здійснивши диференціювання,
У цьому рівнянні є чисто речові та чисто уявні члени (нагадаємо, що S і а речові); прирівнюючи ті та інші окремо нулю, отримаємо два рівняння:

Нехтуючи в першому з цих рівнянь членом, що містить отримаємо
![]() (17,10)
(17,10)
т. е., як і слід, класичне рівняння Гамільтона - Якобі для дії S частки. Ми бачимо, до речі, що при класична механіка справедлива з точністю до величин першого (а не нульового) порядку включно.
Друге з отриманих рівнянь після множення на 2а може бути переписане як
![]()
Це рівняння має наочний фізичний сенс: є густина ймовірності знаходження частки в тому чи іншому місці простору є класична швидкість v частинки. Тому рівняння (17,11) не що інше, як рівняння безперервності, що показує, що щільність ймовірності «переміщається» за законами класичної механіки з класичною швидкістю v у кожній точці.
Завдання
Знайти закон перетворення хвильової функції під час перетворення Галілея.
Рішення. Зробимо перетворення над хвильовою функцією вільного руху частки (плоською хвилею). Оскільки будь-яка функція може бути розкладена за плоским хвиляхтим самим буде знайдено закон перетворення і для довільної хвильової функції.
Плоскі хвилі в системах відліку К і К" (К" рухається відносно До зі швидкістю V):
причому а імпульси та енергії частки в обох системах пов'язані один з одним формулами
(див. I, § 8), Підставивши ці вирази в отримаємо
У такому вигляді ця формула вже не містить величин, що характеризують вільний рухчастинки, та встановлює шуканий загальний законперетворення хвильової функції довільного стану частки. Для системи частинок у показнику експоненти (1) повинна стояти сума по частках.
де – оператор Гамільтона – аналог класичної функції Гамільтона
![]()
в якій і замінені операторами імпульсу x, y, z і координати,,:
x → = x, y → = y, z → = z,
| (4.2) |
Рівняння ШредінгераРівняння Шредінгера, що залежить від часу: де – гамільтоніан системи. Поділ змінних. Запишемо Ψ(,t) = ψ()θ(t), де ψ є функцією координат, а θ – функція часу. Якщо не залежить від часу, тоді рівняння ψ = iћψ набуває вигляду θψ = iћψθ або Ліва частинає функцією лише координат, а права залежить від змінної x. Тому обидві частини останнього рівняння повинні дорівнювати одній і тій же постійній, яку позначимо E
Отже, θ(t) = exp(−iEt/ћ), ψ() = Eψ() та Ψ(,t) = ψ()exp(−iEt/ћ). Рівняння ψ() = Eψ() називають стаціонарним рівнянням Шредінгера. Для одномірної системи з масою m в полі з потенціалом U(x) воно набуває вигляду:
Для тривимірної системиз масою m у полі з потенціалом U(): −(ћ 2 /2m)Δψ() + U()ψ() = Eψ(), де Δ - Лапласіан. |
Так як рівняння Шредінгера є лінійним рівняннямпершого порядку за часом, то з його допомогою за заданим значенням хвильової функції Ψ(x, y, z, 0) у момент часу t = 0 можна знайти її значення у довільний момент часу t − Ψ(x, y, z, t) .
Шредингера для стаціонарного стану, коли потенційна енергія частки не залежить від часу, має вигляд
| ψ() = Eψ(). | (4.3) |
Це рівняння називають стаціонарним рівнянням Шредінгера.
Бо в стаціонарному стані
| Ψ(,t) = ψ()exp(−iEt/ћ) | (4.4) |
і можливість знайти частинку в останній момент t у точці x, y, z пропорційна |Ψ(,t)|, вона ~ |ψ(x,y,z)| 2, тобто. не залежить від часу. Аналогічно, можливість виявити значення фізичної величини, що характеризує систему, також не змінюється з часом, оскільки виражається через квадрат модуля хвильової функції.
4.2. Частка в одновимірній прямокутній ямі з нескінченними стінками
Потенційна енергія U(x) у прямокутній ямі задовольняє наступним умовам:
Частка знаходиться в області 0 ≤ x ≤ L. Поза цією областю ψ(x) = 0. Рівняння Шредінгера для частинки, що знаходиться в області 0 ≤ x ≤ L
де k = (2mE/ћ 2) 1/2 . З граничних умов ψ(0) = 0, ψ(L) = 0 та умов безперервності хвильової функції випливає
Частка може перебувати в одному з безлічі дискретних станів, доступних для неї.
Кожному значенню енергії E n відповідає хвильова функція n (x), яка з урахуванням умови нормування
![]()
має вигляд
|
|
(4.10) |
На відміну від класичної, квантова частка у прямокутній ямі не може мати енергію.
E< ћ 2 π 2 /(2mL 2).
Состояния частицы ψ n в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.

Мал. 4.2. Рівні енергії та хвильові функції частки Ψ у нескінченній прямокутній ямі. Квадрат модуля хвильової функції | 2 визначає ймовірність знаходження частки в різних точкахпотенційної ями.
4.3. Гармонійний осцилятор
Положення рівнів частки потенційної ями залежить від виду потенційної ями. В одновимірній потенційній ямі гармонійного осциляторапотенційна енергія має вигляд
Допустимі значення повної енергії визначаються формулою
| E n = ? 0 (n + 1/2), n = 0, 1, 2, | (4.13) |
На відміну від нескінченної прямокутної ями, спектр рівнів гармонійного осцилятора є еквідистантним.
Зі збільшенням маси частинки або розмірів області її локалізації квантовий опис частки переходить у класичний.
4.4. Частка у полі з центральною симетрією
У сферичних координатах стаціонарне рівнянняШредінгера для частинки у центральному потенціалі U(r) має вигляд
де радіальна функція R nl (r) і кутова функція Y lm (θ,φ), яка називається сферичною, задовольняють рівнянням
| 2 Y lm (θ,φ) = ћ 2 l(l+1)Y lm (θ,φ) | (4.16) |
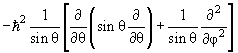 Y lm (θ,φ) = ћ 2 l(l+1)Y lm (θ,φ) Y lm (θ,φ) = ћ 2 l(l+1)Y lm (θ,φ) |
(4.17) |
Рівняння (4.16) визначає можливі власні значення lта власні функції Y lm (θ,φ) оператора квадрата моменту 2 . Рівняння (4.17) визначає власні значення енергії Е та радіальні власні функції R nl (r), від яких залежить енергія системи (рис. 4.3).
Схема рівнів (послідовність та абсолютні значенняенергій) залежить від радіальної функції R nl (r), що у свою чергу визначається потенціалом U(r), в якому знаходиться частка.
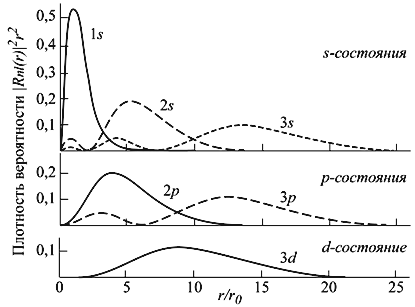
Мал. 4.3. Радіальний розподіл ймовірності знаходження електрона в кулонівському полі протона (атом водню). Відстань дано в борівських радіусах
r 0 = ћ 2 /m e e 2 ≈ 0.529·10 8 cм.
4.5. Орбітальний момент кількості руху
Власні значення L 2 та L z є розв'язком рівнянь
2 Y lm(θ,φ) = L 2 Y lm(θ,φ) та z Y lm(θ,φ) = L z Y lm(θ,φ).
Вони мають такі дискретні значення
L 2 = ћ 2 l(l + 1), де l = 0, 1, 2, 3, …,
L z = m, де m = 0, ± 1, ± 2, ± 3, ..., ± l.
Для характеристики станів з різними значеннямиорбітального моменту l зазвичай використовують такі позначення:
Спектроскопічні назви орбітальних моментів l
| l = 0 | s-стан |
| l = 1 | p-стан |
| l = 2 | d-стан |
| l = 3 | f-стан |
| l = 4 | g-стан |
| l = 5 | h-стан |
| в. т.д. |
Стану з l = 0 відповідає сферично-симетрична хвильова функція. У випадках, коли l ≠ 0 хвильова функція немає сферичної симетрії. Симетрія хвильової функції визначається симетрією сферичних функцій Ylm(θ,φ). Має місце цікаве квантове явище, коли рішення сферично-симетричної задачі (потенціал описує сферично-симетричну систему) призводить до станів, що не мають сферичної симетрії. Таким чином, симетрія рівнянь не обов'язково повинна відображатися в симетрії кожного окремого рішення цих рівнянь, а лише у всій сукупностіцих рішень.
Для частки, що знаходиться у сферично-симетричному потенціалі, величина орбітального моменту кількості руху L:
| (4.18) |
Зазвичай для спрощення, коли говорять про величину орбітального моменту кількості руху, називають цією величиною квантове число l, маючи на увазі, що між l і L є однозначний зв'язок (4.18).
Так як величина l може набувати лише цілочисельних значень 0, 1, 2, 3,…, то й орбітальний момент кількості руху L квантується. Наприклад, для частки з l = 2 момент кількості руху
=
= 6.58·10 -22 √6 МеВ·сек ≈ 2.6·10 - 34 Дж·сек.
Просторове квантування. Орбітальний момент кількості руху векторною величиною. Так як величина орбітального моменту кількості руху квантується, то і напрямок до виділеного напрямку z, наприклад, до зовнішнього магнітному полю, також квантується і набуває дискретних значень Lz = ћm, де m змінюється від +l до –l, тобто має 2l + 1 значень. Наприклад, при l = 2 величина m набуває значень +2, +1, 0, -1, -2 (див. рис. 4.4). Разом про те енергія системи залежить від m, т. е. від напрямку вектора , що є очевидним наслідком сферичної симетрії системи.
Стан частки, що у сферично симетричному полі, повністю описується трьома квантовими числами: n, l і m.
Поява квантових чисел пов'язані з властивостями симетрії системи. Характер цієї симетрії визначає можливі значення квантових чисел. Очевидно, що система, що описується функцією e im φ прийме колишнє значення тільки тоді, коли азимутальний кут φ в результаті повороту навколо осі z прийме колишнє значення φ. Цій умові функція e im φ задовольняє лише тоді, коли величина mφ кратна 2π. Тобто. величина m повинна мати цілі значення. Так як необхідно враховувати обертання у двох протилежних напрямках та відсутність обертання, єдино можливими значеннями виявляються m = 0, ±1, ±2, ….
4.6. Спін
Спин – власний момент кількості руху частки. Між значенням вектора спина і квантовим числом спина s виконується таке співвідношення, як між величиною значенням вектора орбітального моменту і орбітальним квантовим числом l:
| 2 = 2 s(s + 1) | (4.19) |
На відміну від орбітального квантового числа l, яке може бути лише цілим числом або нулем, спінове квантове число s (надалі просто спин) може бути як цілим (включаючи нуль), так і напівцілим, тобто s = 0, 1/ 2, 1, 3/2, 2, 5/2, …, але при цьому для кожного елементарної часткиспин може приймати єдине властиве цьому типу частинок значення. Так, спини π-мезонів і К-мезонів дорівнюють 0. Спини електрона, протона, нейтрино, кварків та їх античастинок дорівнюють 1/2. Спин фотона дорівнює 1. Бозони становлять клас частинок із цілим значенням спина, спин ферміонів має напівціле значення. Спин частинки неможливо змінити, як і її заряд чи масу. Це її стала квантова характеристика.
Як і у разі інших квантових векторів, проекція вектора спина на будь-який фіксований напрямок у просторі (наприклад, на вісь z) може набувати 2s + 1 значення:
s z ћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ,..., ±1/2ћ або 0.
Число s z – це квантове число проекції спина. Максимальна величина s z збігається із s. Оскільки спин електрона дорівнює 1/2, то проекція цього спина може набувати лише два значення s z = ±1/2. Якщо проекція +1/2, то кажуть, що спин спрямований нагору, якщо проекція -1/2, то кажуть, що спин спрямований вниз.
4.7. Повний момент кількості руху
Повний момент кількості руху частинки або системи частинок є векторною сумою орбітального та спінового моментів кількості руху.
Квадрат повного моменту має значення:
2 = ћ 2 j(j + 1).
Квантове число повного моменту j, що відповідає сумі двох векторів і може приймати ряд дискретних значень, що відрізняються на 1:
j = l + s, l + s −1,..., |l − s|
Проекція на виділену вісь J z також набуває дискретних значень:
J z = ћj z; = -j, -j + 1, ..., j - 1, j.
Число значень проекції J z дорівнює 2j + 1. Якщо і визначені єдині значення проекцій на вісь z l z і s z , то j z також визначена однозначно: j z = l z + s z .
4.8. Квантові числа
Квантові числа – це цілі чи дробові числа, Які визначають всі можливі значення фізичної величини, що характеризує різні квантові системи - атоми, атомні ядра, кварки та інші частки.
Таблиця квантових чисел
| n | Радіальне квантове число.Визначає кількість вузлів хвильової функції та енергію системи. n = 1, 2, …, ∞. |
| J, j | Повний кутовий момент J та його квантове число j. Останнє ніколи не буває негативним і може бути цілим або напівцілим залежно від властивостей системи, що розглядається. 2 = ћ 2 j(j + 1). |
| L, l | Орбітальний кутовий момент L та його квантове число l. Інтерпретація l така сама, як j, але l може набувати лише цілі значення, включаючи нуль: l = 0, 1, 2,…. L 2 = 2 l (l + 1). |
| m | Магнітне квантове число.Проекція повного або орбітального кутового моменту на виділену вісь (зазвичай вісь z) дорівнює mћ. Для повного моменту m = ±j, ±(j-1), …, ±1/2 або 0. Для орбітального m = ±l, ±(l-1), …, ±1, 0. |
| S, s | Спиновий кутовий момент S та його квантове число s. Воно може бути або позитивним цілим (включаючи нуль) або напівцілим. s - Постійна характеристика частки певного типу. S 2 = 2 s(s + 1). |
| s z | Квантова кількість проекції спинового моментучастинки на виділену вісь. Ця проекція може набувати значень s z ћ, де s z = ± s, ± (s -1), …, ±1/2 або 0. |
| P або π | Просторова парність.Характеризує поведінку системи за просторової інверсії → - (дзеркальне відображення). Повна парність частинки Р = π(-1) l , де π – її внутрішня парність, а (-1) l – її орбітальна парність. Внутрішні парності кварків позитивні, антикварків – негативні. |
| I | Ізопін.Характеризує властивість зарядової інваріантності сильних взаємодій |
Для позначення спінового моменту часто використовують літеру J.
Усі стани, в яких може перебувати квантова система, описуються за допомогою повного наборуквантових чисел. Так у разі протона в ядрі стан протона описується за допомогою чотирьох квантових чисел, що відповідають чотирма ступенями свободи – трьома просторовими координатами і спиною. Це
- Радіальне квантове число n (1, 2, …, ∞),
- Орбітальне квантове число l (0, 1, 2, …),
- Проекція орбітального моменту m (± l, ± (l-1), …, ±1, 0),
- Спин протону s = 1/2.
Для опису сферично-симетричних систем квантової фізикивикористовуються різні сферично-симетричні потенціали з різною радіальною залежністю:
![]()
де U 0 а і R - позитивні константи (R - радіус ядра). У всіх випадках сферично симетричні системи можна описати за допомогою набору квантових чисел n, l, j, j z, однак, залежно від радіального виду потенціалу, енергетичний спектр станів системи буде різним.
Існування збережених у часі фізичних величинтісно пов'язане із властивостями симетрії гамільтоніана системи. Наприклад, у випадку, якщо квантова система має центральною симетрією U = U(r), то цій системі відповідає збереження орбітального моменту кількості руху l та однієї з його проекцій m. При цьому через сферичну симетрію завдання енергія станів не залежатиме від величини m, тобто стану будуть виродженими по m.
Поряд з просторовими симетріями, пов'язаними з безперервними перетвореннями, у квантовій фізиці існують інші симетрії – дискретні. Однією з них є дзеркальна симетріяхвильової функції щодо інверсії координат (→-). Оператору інверсії відповідає квантове число парність, яке може набувати два значення +1 і -1 залежно від того, чи зберігається знак хвильової функції при інверсії чи змінюється на протилежний.
Система тотожних частинок характеризується ще однією симетрією – симетрією щодо перестановок тотожних частинок. Ця симетрія визначається властивостями частинок, що утворюють систему. Системи частинок із цілим спином (бозонів) описуються симетричними хвильовими функціями, системи частинок із напівцілим спином (ферміонів) – антисиметричними хвильовими функціями.
Загальне рівняння Шредінгера. Шредінгера для стаціонарних станів
Статистичне тлумачення хвиль де Бройля (див. § 216) та співвідношення невизначеностей Гейзенберга (див. 5 215) привели до висновку, що рівнянням руху в квантовій механіці, що описує рух мікрочастинок у різних силових поляхмає бути рівняння, з якого випливали б спостерігаються на досвіді хвильові властивостічастинок. Основне рівняння має бути рівнянням щодо хвильової функції Ψ (х, у, z, t), оскільки саме вона, чи, точніше, величина |Ψ| 2 визначає ймовірність перебування частки в момент часу t в обсязі dV, тобто в області з координатами x і x + dx, y і y + dy, z і z + dz. Оскільки шукане рівняння має враховувати хвильові властивості частинок, воно має бути хвильовим рівнянням, подібно до рівняння, що описує електромагнітні хвилі.
Основне рівняння нерелятивістської квантової механіки сформульовано 1926 р. е. Шредінгером. Рівняння Шредінгера, як і всі основні рівняння фізики (наприклад, рівняння Ньютона в класичній механіці та рівняння Максвелла для електромагнітного поля), не виводиться, а постулюється. Правильність цього рівняння підтверджується згодою з досвідом одержуваних з його допомогою результатів, що, своєю чергою, надає йому характеру закону природи. Рівняння Шредінгера має вигляд
де h=h/(2π), m-маса частинки, ∆-оператор Лапласа (  ),
),
i - уявна одиниця, U (х, у, z, t) - потенційна функція частки у силовому полі, в якому вона рухається, Ψ (х, у, z, t ) - потрібна хвильова функція частинки.
Рівняння (217.1) справедливе для будь-якої частинки (зі спином, рівним 0; див. § 225), що рухається з малою (порівняно зі швидкістю світла) швидкістю, тобто зі швидкістю υ<<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной (см. § 216); 2) производные

повинні бути безперервними; 3) функція |Ψ| 2 має бути інтегрована; ця умова у найпростіших випадках зводиться до умови нормування ймовірностей (216.3).
Щоб прийти до рівняння Шредінгера, розглянемо частину, що вільно рухається, якій, згідно ідеї де Бройля, зіставляється плоска хвиля. Для простоти розглянемо одновимірний випадок. Рівняння плоскої хвилі, що розповсюджується вздовж осі х, має вигляд (див. § 154)
Або в комплексному записі ![]() . Отже, плоска хвиля де Бройля має вигляд
. Отже, плоска хвиля де Бройля має вигляд
![]() (217.2)
(217.2)
(враховано, що = E/h, k=p/h). У квантовій механіці показник експоненти беруть зі знаком мінус, але оскільки фізичне значення має тільки |Ψ| 2 , це (див. (217.2)) несуттєво. Тоді
 ,
,
 ; (217.3)
; (217.3)
Використовуючи взаємозв'язок між енергією Е та імпульсом p (E = p 2 /(2m)) та підставляючи вирази (217.3), отримаємо диференціальне рівняння

яке збігається з рівнянням (217.1) для випадку U = 0 (ми розглядали вільну частинку).
Якщо частка рухається в силовому полі, що характеризується потенційною енергією U, то повна енергія Е складається з кінетичної та потенційної енергії. Проводячи аналогічні міркування використовуючи взаємозв'язок між Еі р (для цього випадку р 2 /(2m)=E -U), пасмо до диференціального рівняння, що збігається з (217.1).
Наведені міркування не повинні сприйматися як висновок рівняння Шредінгера. Вони лише пояснюють, як можна дійти цього рівняння. Доказом правильності рівняння Шредінгера є згода з досвідом висновків, до яких воно призводить.
Рівняння (217.1) є загальним рівнянням Шредінгера. Його також називають рівнянням Шредінгера, що залежить від часу. Для багатьох фізичних явищ, що відбуваються в мікросвіті, рівняння (217.1) можна спростити, виключивши залежність від часу, іншими словами, знайти рівняння Шредінгера для стаціонарного стану - стан з фіксованими значеннями енергії. Це можливо, якщо силове поле, в якому частка рухається, стаціонарно, тобто функція U = U(х, у, z ) не залежить явно від часу та має сенс потенційної енергії. В даному випадку рішення рівняння Шредінгера може бути представлене у вигляді добутку двох функцій, одна з яких є функція лише координат, інша - лише часу, причому залежність від часу виражається множником
![]() ,
,
де Е - повна енергія частки, постійна у разі стаціонарного поля. Підставляючи (217.4) у (217.1), отримаємо
звідки після розподілу на загальний множник е – i (E/h) t і відповідних перетворень прийдемо до рівняння, що визначає функцію ψ:
![]() (217.5)
(217.5)
Рівняння (217.5) називається рівнянням Шредінгера для стаціонарних станів.
До цього рівняння як параметр входить повна енергія Е частинки. Теоретично диференціальних рівнянь доводиться, що такі рівняння мають безліч рішень, у тому числі у вигляді накладання граничних умов відбирають рішення, мають фізичний смысл. Для рівняння Шредінгера такими умовами є умови регулярності хвильових функцій: хвильові функції мають бути кінцевими, однозначними і безперервними разом із першими похідними. Таким чином, реальний фізичний сенс мають лише такі рішення, що виражаються регулярними функціями ψ . Але регулярні рішення мають місце не за будь-яких значень параметра Е, а лише за певного їх набору, характерному для даної задачі. Ці значення енергії називаються власними. Рішення ж, які відповідають власним значенням енергії, називаються власними функціями. Власні значення Е можуть утворювати як безперервний, і дискретний ряд. У першому випадку говорять про безперервний, або суцільний, спектр, у другому - про дискретний спектр.
У розвиток ідеї де-Бройля про хвильові властивості речовини Е. Шредінгер отримав у 1926 р. своє знамените рівняння. Шредінгер зіставив руху мікрочастинки комплексну функцію координат і часу, яку він назвав хвильовою функцією і позначив грецькою літерою "псі" (). Ми називатимемо її псі-функцією.
Псі-функція характеризує стан мікрочастинки. Вигляд функції виходить з рішення рівняння Шредінгера, яке виглядає наступним чином:
Тут - маса частинки, i - уявна одиниця, - оператор Лапласа, результат дії якого на деяку функцію є сумою інших приватних похідних за координатами:
![]()
Літерою U у рівнянні (21.1) позначено функцію координат і часу, градієнт якої, взятий зі зворотним знаком, визначає силу, що діє на частинку. У випадку, коли функція U не залежить від часу, вона має сенс потенційної енергії частки.
З рівняння (21.1) слід, що вид пси-функции визначається функцією U, т. е. зрештою характером сил, які діють частка.
Рівняння Шредінгера є основним рівнянням нерелятивістської квантової механіки. Воно може бути виведено з інших співвідношень. Його слід розглядати як вихідне основне припущення, справедливість якого доводиться тим, що всі слідства, що випливають з нього, найточніше узгоджуються з досвідченими фактами.
Шредінгер встановив своє рівняння, виходячи з оптико-механічної аналогії. Ця аналогія полягає у схожості рівнянь, що описують хід світлових променів, з рівняннями, що визначають траєкторії частинок в аналітичній механіці. В оптиці хід променів задовольняє принцип Ферма (див. § 115 2-го тому), в механіці вид траєкторії задовольняє так званому принципу найменшої дії.
Якщо силове поле, в якому рухається частка, стаціонарно, то функція V не залежить явно від часу і має, як зазначалося, сенс потенційної енергії. У цьому випадку рішення рівняння Шредінгера розпадається на два множники, один з яких залежить тільки від координат, інший - тільки від часу:
Тут Е – повна енергія частки, яка у разі стаціонарного поля залишається постійною. Щоб переконатися у справедливості виразу (21.3), підставимо його до рівняння (21.1). В результаті отримаємо співвідношення
Скоротивши на загальний множник прийдемо до диференціального рівняння, що визначає функцію
Рівняння (21.4) називається рівнянням Шредінгера для стаціонарних станів. Надалі ми матимемо справу тільки з цим рівнянням і для стислості називатимемо його просто рівнянням Шредінгера. Рівняння (21.4) часто пишуть у вигляді
![]()
Пояснимо, як можна дійти рівняння Шредінгера. Для простоти обмежимося одновимірним випадком. Розглянемо вільно рухому частинку.
Відповідно до ідеї де-Бройля їй потрібно зіставити плоску хвилю
(У квантовій механіці прийнято показник експоненти брати зі знаком мінус). Замінивши відповідно до (18.1) і (18.2) через Е і , прийдемо до виразу
Продиференціювавши цей вираз один раз по t, а вдруге двічі по х отримаємо
У нерелятивістській класичній механіці енергія Е та імпульс вільної частки пов'язані співвідношенням
Підставивши в це співвідношення виразу (21.7) для Е і скоротивши потім на , отримаємо рівняння
![]()
яке збігається з рівнянням (21.1), якщо в останньому покласти
У разі частинки, що рухається в силовому полі, що характеризується потенційною енергією U, енергія Е та імпульс пов'язані співвідношенням
![]()
Поширивши і цей випадок висловлювання (21.7) для Е й отримаємо
Помноживши це співвідношення на , перенісши член вліво, прийдемо до рівняння
збігається з рівнянням (21.1).
Викладені міркування немає доказової сили не можуть розглядатися як висновок рівняння Шредінгера. Їхня мета - пояснити, яким чином можна було прийти до встановлення цього рівняння.
У квантової механіки велику роль грає поняття Під оператором розуміють правило, з якого однієї функції (позначимо її) зіставляється інша функція (позначимо її). Символічно це записується так:
Тут - символічне позначення оператора (з таким самим успіхом можна було взяти будь-яку іншу літеру з «капелюшком» над нею, наприклад тощо). У формулі (21.2) роль Q відіграє роль – функція F, а роль f – права частина формули.

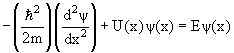 або
або 

