Як знайти декартові координати Декартові координати точок площини

Упорядкована система двох або трьох перетинаються перпендикулярний другдругові осей з загальним початкомвідліку (початком координат) та загальною одиницеюдовжини називається прямокутною декартовою системою координат .

Загальна декартова система координат (афінна система координат) може містити і не обов'язково перпендикулярні осі. На честь французького математика Рене Декарта (1596-1662) названо саме таку систему координат, у якій усім осях відраховується загальна одиниця довжини і осі є прямими.

Прямокутна декартова система координат на площині має дві осі, а прямокутна декартова система координат у просторі - Три осі. Кожна точка на площині чи просторі визначається упорядкованим набором координат - чисел відповідно до одиниці довжини системи координат.

Зауважимо, що, як випливає з визначення, існує декартова система координат і на прямій, тобто в одному вимірі. Введення декартових координат на прямий є одним із способів, за допомогою якого будь-якій точці прямий ставиться у відповідність цілком певне речове число, тобто координата.

Метод координат, що у роботах Рене Декарта, ознаменував собою революційну перебудову всієї математики. З'явилася можливість тлумачити алгебраїчні рівняння(або нерівності) у вигляді геометричних образів (графіків) і, навпаки, шукати рішення геометричних завданьза допомогою аналітичних формул, систем рівнянь. Так, нерівність z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатної площини xOyта перебуває вище цієї площини на 3 одиниці.

За допомогою декартової системи координат належність точки заданої кривої відповідає тому, що числа xі yзадовольняють деякому рівнянню. Так, координати точки кола з центром в заданій точці (a; b) задовольняють рівняння (x - a)² + ( y - b)² = R² .

Прямокутна декартова система координат на площині

Дві перпендикулярні осі на площині із загальним початком та однаковою масштабною одиницею утворюють декартову прямокутну систему координат на площині . Одна з цих осей називається віссю Ox, або віссю абсцис , іншу - віссю Ой, або віссю ординат . Ці осі називаються також координатними осями. Позначимо через Mxі Myвідповідно проекції довільної точки Мна осі Oxі Ой. Як отримати проекцію? Проведемо через точку М Ox. Ця пряма перетинає вісь Oxу точці Mx. Проведемо через точку Мпряму, перпендикулярну до осі Ой. Ця пряма перетинає вісь Ойу точці My. Це показано нижче.

xі yкрапки Мназиватимемо відповідно величини спрямованих відрізків OMxі OMy. Величини цих спрямованих відрізків розраховуються відповідно як x = x0 - 0 і y = y0 - 0 . Декартові координати xі yкрапки М абсцисою і ординатою . Той факт, що точка Ммає координати xі y, позначається так: M(x, y) .

Координатні осі розбивають площину на чотири квадранта нумерація яких показана на малюнку нижче. На ньому вказана розстановка знаків координат точок залежно від їх розташування в тому чи іншому квадранті.

Крім декартових прямокутних координат на площині, часто розглядається також полярна система координат. Про спосіб переходу від однієї системи координат до іншої – в уроці полярна система координат .

Прямокутна декартова система координат у просторі

Декартові координати у просторі вводяться у повній аналогії з декартовими координатами на площині.

Три взаємно перпендикулярні осі у просторі (координатні осі) із загальним початком Oі однаковою масштабною одиницею утворюють декартову прямокутну систему координат у просторі .

Одну із зазначених осей називають віссю Ox, або віссю абсцис , іншу - віссю Ой, або віссю ординат третю - віссю Oz, або віссю аплікат . Нехай Mx, My Mz- Проекції довільної точки Мпростору на осі Ox , Ойі Ozвідповідно.

Проведемо через точку М OxOxу точці Mx. Проведемо через точку Мплощину, перпендикулярну до осі Ой. Ця площина перетинає вісь Ойу точці My. Проведемо через точку Мплощину, перпендикулярну до осі Oz. Ця площина перетинає вісь Ozу точці Mz.

Декартові прямокутні координати x , yі zкрапки Мназиватимемо відповідно величини спрямованих відрізків OMx, OMyі OMz. Величини цих спрямованих відрізків розраховуються відповідно як x = x0 - 0 , y = y0 - 0 і z = z0 - 0 .

Декартові координати x , yі zкрапки Мназиваються відповідно до неї абсцисою , ординатою і аплікати .

Попарно взяті координатні осі розташовуються в координатних площинах. xOy , yOzі zOx .

Завдання про точки в декартовій системі координат

приклад 1.

A(2; -3) ;

B(3; -1) ;

C(-5; 1) .

Знайти координати проекцій цих точок на вісь абсцис.

Рішення. Як випливає з теоретичної частини цього уроку, проекція точки на вісь абсцис розташована на самій осі абсцис, тобто осі Ox, а отже має абсцису, рівну абсцисі самої точки, і ординату (координату на осі Ой, яку вісь абсцис перетинає у точці 0), рівну нулю. Отже отримуємо наступні координати даних точок на вісь абсцис:

Ax (2; 0);

Bx (3; 0);

Cx (-5; 0).

приклад 2.У декартовій системі координат на площині дані точки

A(-3; 2) ;

B(-5; 1) ;

C(3; -2) .

Знайти координати проекцій цих точок на вісь ординат.

Рішення. Як випливає з теоретичної частини цього уроку, проекція точки на вісь ординат розташована на осі ординат, тобто осі Ой, а отже має ординату, рівну ординаті самої точки, та абсцису (координату на осі Ox, Яку вісь ординат перетинає в точці 0), рівну нулю. Отже отримуємо наступні координати даних точок на вісь ординат:

Ay (0; 2);

By (0; 1);

Cy (0; -2).

приклад 3.У декартовій системі координат на площині дані точки

A(2; 3) ;

B(-3; 2) ;

C(-1; -1) .

Ox .

Ox Ox Ox, матиме таку ж абсцису, що і дана точка, і ординату, що дорівнює абсолютної величиниординаті цієї точки, і протилежну їй за знаком. Отже, отримуємо наступні координати точок, симетричних цим точкам щодо осі. Ox :

A"(2; -3) ;

B"(-3; -2) ;

C"(-1; 1) .

Вирішити завдання на декартову систему координат самостійно, а потім переглянути рішення

приклад 4.Визначити, у яких квадрантах (чвертях, малюнок з квадрантами - наприкінці параграфа "Прямокутна декартова система координат на площині") може бути розташована точка M(x; y) , якщо

1) xy > 0 ;

2) xy < 0 ;

3) x − y = 0 ;

4) x + y = 0 ;

5) x + y > 0 ;

6) x + y < 0 ;

7) x − y > 0 ;

8) x − y < 0 .

Приклад 5.У декартовій системі координат на площині дані точки

A(-2; 5) ;

B(3; -5) ;

C(a; b) .

Знайти координати точок, симетричних цим точкам щодо осі Ой .

Продовжуємо вирішувати завдання разом

Приклад 6.У декартовій системі координат на площині дані точки

A(-1; 2) ;

B(3; -1) ;

C(-2; -2) .

Знайти координати точок, симетричних цим точкам щодо осі Ой .

Рішення. Повертаємо на 180 градусів навколо осі Ойспрямований відрізок, що йде від осі Ойдо цієї точки. На малюнку, де позначені квадранти площини, бачимо, що точка, симетрична даної щодо осі Ой, матиме таку ж ординату, що і дана точка, і абсцису, рівну за абсолютною величиною абсцис даної точки, і протилежну їй за знаком. Отже, отримуємо наступні координати точок, симетричних цим точкам щодо осі. Ой :

A"(1; 2) ;

B"(-3; -1) ;

C"(2; -2) .

Приклад 7.У декартовій системі координат на площині дані точки

A(3; 3) ;

B(2; -4) ;

C(-2; 1) .

Знайти координати точок, симетричних цим точкам щодо початку координат.

Рішення. Повертаємо на 180 градусів навколо початку координат спрямований відрізок, що йде від початку координат до цієї точки. На малюнку, де позначені квадранти площини, бачимо, що точка, симетрична даної щодо початку координат, матиме абсцису та ординату, рівні за абсолютною величиною абсцисі та ординаті даної точки, але протилежні їм за знаком. Отже отримуємо наступні координати точок, симетричних цим точкам щодо початку координат:

A"(-3; -3) ;

B"(-2; 4) ;

C(2; -1) .

Приклад 8.

A(4; 3; 5) ;

B(-3; 2; 1) ;

C(2; -3; 0) .

Знайти координати проекцій цих точок:

1) на площину Oxy ;

2) на площину Oxz ;

3) на площину Oyz ;

4) на вісь абсцис;

5) на вісь ординат;

6) на вісь аплікат.

1) Проекція точки на площину Oxyрозташована на цій площині, а отже має абсцису і ординату, рівні абсцисі і ординаті даної точки, і аплікату, рівну нулю. Отже, отримуємо наступні координати проекцій даних точок на Oxy :

Axy (4; 3; 0);

Bxy (-3; 2; 0);

Cxy (2; -3; 0).

2) Проекція точки на площину Oxzрозташована на цій площині, а отже має абсцису і аплікату, рівні абсцисі і аплікату даної точки, і ординату, рівну нулю. Отже, отримуємо наступні координати проекцій даних точок на Oxz :

Axz (4; 0; 5);

Bxz (-3; 0; 1);

Cxz (2; 0; 0).

3) Проекція точки на площину Oyzрозташована на цій площині, а отже має ординату і аплікату, рівні ординаті і аплікату даної точки, і абсцису, рівну нулю. Отже, отримуємо наступні координати проекцій даних точок на Oyz :

Ayz (0; 3; 5);

Byz (0; 2; 1);

Cyz (0; -3; 0).

4) Як випливає з теоретичної частини цього уроку, проекція точки на вісь абсцис розташована на самій осі абсцис, тобто осі Ox, а отже має абсцису, рівну абсцисі самої точки, а ордината і апліката проекції дорівнюють нулю (оскільки осі ординат і аплікат перетинають вісь абсцис у точці 0). Отримуємо наступні координати проекцій даних точок на вісь абсцис:

Ax (4; 0; 0);

Bx (-3; 0; 0);

Cx (2; 0; 0).

5) Проекція точки на вісь ординат розташована на самій осі ординат, тобто осі Ой, а отже має ординату, рівну ординаті самої точки, а абсцису та аплікату проекції дорівнюють нулю (оскільки осі абсцис і аплікат перетинають вісь ординат у точці 0). Отримуємо наступні координати проекцій даних точок на вісь ординат:

Ay (0; 3; 0);

By (0; 2; 0);

Cy (0; -3; 0).

6) Проекція точки на вісь аплікат розташована на самій осі аплікат, тобто осі Oz, а отже має аплікату, рівну аплікату самої точки, а абсцису та ординату проекції дорівнюють нулю (оскільки осі абсцис та ординат перетинають вісь аплікат у точці 0). Отримуємо наступні координати проекцій даних точок на вісь аплікат:

Az (0; 0; 5);

Bz (0; 0; 1);

Cz (0; 0; 0).

Приклад 9.У декартовій системі координат у просторі дані точки

A(2; 3; 1) ;

B(5; -3; 2) ;

C(-3; 2; -1) .

Знайти координати точок, симетричних цим точкам щодо:

1) площині Oxy ;

2) площині Oxz ;

3) площині Oyz ;

4) осі абсцис;

5) осі ординат;

6) осі аплікат;

7) початку координат.

1) "Просуваємо" точку з іншого боку осі Oxy Oxy, матиме абсцису та ординату, рівні абсцисі та ординаті даної точки, і аплікату, рівну за величиною аплікату даної точки, але протилежну їй за знаком. Отже, отримуємо наступні координати точок, симетричних даних щодо площини Oxy :

A"(2; 3; -1) ;

B"(5; -3; -2) ;

C"(-3; 2; 1) .

2) "Просуваємо" точку з іншого боку осі Oxzна ту ж відстань. По малюнку, що відображає координатний простір, бачимо, що точка, симетрична даної щодо осі Oxz, матиме абсцису та аплікату, рівні абсцисі та аплікату даної точки, і ординату, рівну за величиною ординаті даної точки, але протилежну їй за знаком. Отже, отримуємо наступні координати точок, симетричних даних щодо площини Oxz :

A"(2; -3; 1) ;

B"(5; 3; 2) ;

C"(-3; -2; -1) .

3) "Просуваємо" точку з іншого боку осі Oyzна ту ж відстань. По малюнку, що відображає координатний простір, бачимо, що точка, симетрична даної щодо осі Oyz, матиме ординату і аплікату, рівні ординаті та аплікату даної точки, і абсцису, рівну за величиною абсцисі даної точки, але протилежну їй за знаком. Отже, отримуємо наступні координати точок, симетричних даних щодо площини Oyz :

A"(-2; 3; 1) ;

B"(-5; -3; 2) ;

C"(3; 2; -1) .

За аналогією з симетричними точкамина площині та точками простору, симетричними даними щодо площин, зауважуємо, що у разі симетрії щодо деякої осі декартової системи координат у просторі, координата на осі, щодо якої задана симетрія, збереже свій знак, а координати на двох інших осях будуть тими ж абсолютною величині, як і координати цієї точки, але протилежними за знаком.

4) Свій знак збереже абсцису, а ордината та апліката поміняють знаки. Отже, отримуємо наступні координати точок, симетричних даним щодо осі абсцис:

A"(2; -3; -1) ;

B"(5; 3; -2) ;

C"(-3; -2; 1) .

5) Свій знак збереже ордината, а абсцису та аплікату поміняють знаки. Отже, отримуємо наступні координати точок, симетричних даним щодо осі ординат:

A"(-2; 3; -1) ;

B"(-5; -3; -2) ;

C"(3; 2; 1) .

6) Свій знак збереже апліката, а абсциса та ордината поміняють знаки. Отже, отримуємо наступні координати точок, симетричних даних щодо осі:

A"(-2; -3; 1) ;

B"(-5; 3; 2) ;

C"(3; -2; -1) .

7) За аналогією з симетрією у випадку з точками на площині, у разі симетрії щодо початку координат всі координати точки, симетричної даної, будуть рівними за абсолютною величиною координат цієї точки, але протилежними їм за знаком. Отже, отримуємо наступні координати точок, симетричних даних щодо початку координат.

Визначення 1 . Числовою віссю ( числової прямої, координатної прямої) Ox називають пряму лінію, на якій точка O обрана початком відліку (початком координат)(рис.1), напрямок

O → x

вказано як позитивного спрямуванняі відзначено відрізок, довжина якого прийнята за одиницю довжини.

Визначення 2 . Відрізок, довжина якого прийнята за одиницю довжини називають масштабом .

Кожна точка числової осі має координату речовим числом. Координата точки O дорівнює нулю. Координата довільної точки A, що лежить на промені Ox, дорівнює довжині відрізка OA. Координата довільної точки A числової осі, що не лежить на промені Ox негативна, а по абсолютній величині дорівнює довжині відрізка OA .

Визначення 3 . Прямокутною декартовою системою координат Oxy на площиніназивають дві взаємно перпендикулярнихчислових осі Ox і Oy з однаковими масштабамиі загальним початком відлікуу точці O , причому таких, що поворот від променя Ox на кут 90 ° до променя Oy здійснюється у напрямку проти ходу годинникової стрілки(Рис.2).

Зауваження. Прямокутну декартову систему координат Oxy , зображену малюнку 2, називають правою системою координат, на відміну від лівих систем координат, В яких поворот променя Ox на кут 90 ° до променя Oy здійснюється в напрямку по ходу годинникової стрілки. У цьому довіднику ми розглядаємо лише праві системи координат, не обговорюючи цього особливо.

Якщо на площині ввести якусь систему прямокутних декартових координат Oxy, то кожна точка площини придбає дві координати – абсцисуі ординату, що обчислюються таким чином. Нехай A – довільна точка площини. Опустимо з точки A перпендикуляри AA 1 та AA 2 на прямі Ox та Oy відповідно (рис.3).

Визначення 4 . Абсцисою точки A називають координату точки A 1 на числовій осі Ox , ординатою точки A називають координату точки A 2 на числовій осі Oy.

Позначення. Координати (абсцису та ординату) точки A у прямокутній декартовій системі координат Oxy (рис.4) прийнято позначати A(x;y) або A = (x; y).

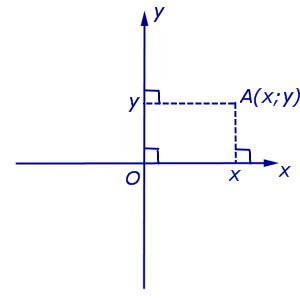
Зауваження. Точка O, звана початком координат, має координати O(0 ; 0) .

Визначення 5 . У прямокутній декартовій системі координат Oxy числову вісь Ox називають віссю абсцис, а числову вісь Oy називають віссю ординат (рис. 5).

Визначення 6 . Кожна прямокутна декартова система координат ділить площину на 4 чверті (квадранту), нумерація яких показана малюнку 5.

Визначення 7 . Площина, на якій задана прямокутна декартова система координат, називають координатною площиною.

Зауваження. Вісь абсцис задається на координатній площині рівнянням y= 0 , вісь ординат задається на координатній площині рівнянням x = 0.

Твердження 1 . Відстань між двома точкамикоординатної площини

A 1 (x 1 ;y 1) і A 2 (x 2 ;y 2)

обчислюється за формулою

Доведення . Розглянемо рисунок 6.

Отже,

що й потрібно було довести.

Рівняння кола на координатній площині

Розглянемо на координатній площині Oxy (рис. 7) коло радіуса R із центром у точці A 0 (x 0 ;y 0) .

Полярні координати

Число називають полярним радіусомточки або першою полярною координатою. Відстань може бути негативним, тому полярний радіус будь-якої точки . Першу полярну координату також позначають грецькою літерою(«ро»), але я звик до латинського варіанту, і надалі використовуватиму його.

Число називають полярним кутомданої точки або другою полярною координатою. Полярний кут стандартно змінюється в межах (так звані головні значення кута). Однак цілком допустимо використовувати діапазон , а в деяких випадках взагалі виникає пряма необхідність розглянути всі значення кута від нуля до «плюс нескінченності». Рекомендую, до речі, звикнути до радіанної міри кута, оскільки оперувати градусами в вищої математикивважається не комільфо.

Пару називають полярними координатамиточки. З легко знайти і їх конкретні значення. Тангенс гострого кутапрямокутного трикутника - є відношення протилежного катетадо прилеглого катету: , отже, сам кут: . За теоремою Піфагора, квадрат гіпотенузи дорівнює суміквадратів катетів: отже, полярний радіус:

Таким чином, .

Один пінгвін добре, а зграя - краще:


Негативно орієнтовані кути я про всяк випадок відзначив стрілками, раптом хтось із читачів ще не знав про цю орієнтацію. За бажання можна «прикрутити» до кожного з них 1 оборот (рад. або 360 градусів) і отримати, до речі, зручні табличні значення:

Але недолік цих «традиційно» орієнтованих кутів полягає в тому, що вони надто далеко (більш ніж на 180 градусів) «закручені» проти годинникової стрілки. Передчуваю питання: «чому нестача і навіщо взагалі потрібні якісь негативні кути?» У математиці цінуються найкоротші та раціональні шляхи. Ну а вже з погляду фізики напрям обертання найчастіше має принципове значення – кожен із нас намагався відчинити двері, смикаючи ручку не в той бік.

Порядок та техніка побудови точок у полярних координатах

Красиві картинки красиві, проте побудова в полярної системикоординат - заняття досить копітке. Труднощів не виникає з точками, у яких полярні кути становлять , у нашому прикладі це точки ; Особливих турбот також не завдають значення, кратні 45 градусам: . Але як правильно і грамотно побудувати, скажімо, точку?

Потрібний картатий листок паперу, олівець і наступні креслярські інструменти: лінійка, циркуль, транспортир. У крайньому випадку, Можна обійтися однією лінійкою, а то ... і зовсім без неї! Читайте далі і ви отримаєте ще один доказ, що ця країна є непереможною =)

Приклад 1

Побудувати точку у полярній системі координат.

Насамперед, необхідно з'ясувати градусний західкута. Якщо кут малознаком або є сумніви, то завжди краще скористатися таблицеюабо загальною формулою переведення радіанів у градуси. Отже, наш кут складає (або ).

Накреслимо полярну систему координат (див. початок уроку) і візьмемо до рук транспортир. Власникам круглого інструменту не важко відзначити 240 градусів, але з великою ймовірністю у вас на руках буде напівкругла версія девайсу. Проблема повної відсутності транспортира за наявності принтера та ножиць вирішується рукоділлям.

Є два шляхи: перевернути листок і відзначити 120 градусів, або «прикрутити» підлогу обороту та розглянути протилежний кут. Виберемо дорослий спосіб і зробимо позначку 60 градусів:


Чи транспортир ліліпутський, чи клітина гігантська =) Втім, щоб відміряти кут масштаб не важливий.

Проводимо олівцем тонку пряму, що проходить через полюс і зроблену відмітку:


З кутом розібралися на черзі полярний радіус. Беремо циркуль та по лінійцівстановлюємо його розчин у 3 одиниці, найчастіше це, звичайно ж, сантиметри:

Тепер акуратно встановлюємо голку на полюс, та обертальним рухомвиконуємо невелику засічку (червоний колір). Шукана точка побудована:


Можна обійтися без циркуля, приклавши лінійку безпосередньо до збудованої прямої та відмірявши 3 сантиметри. Але, як ми побачимо пізніше, у завданнях на побудову у полярній системі координаттипова ситуація, коли потрібно відзначити дві або Велика кількістьточок з тим самим полярним радіусом, тому ефективніше гартувати метал. Зокрема, на нашому кресленні, розгорнувши ногу циркуля на 180 градусів, легко зробити другу засічку та побудувати симетричну щодо полюса точку. На ній давайте і відпрацюємо матеріал наступного параграфа:

Взаємозв'язок прямокутної та полярної системи координат

Очевидним чином приєднаємодо полярної системи координат «звичайну» координатну сітку і зобразимо на кресленні точку :

Таке приєднання завжди корисно пам'ятати, коли виконуєте креслення в полярних координатах. Хоча, хоч-не-хоч воно напрошується і без зайвого натяку.

Встановимо взаємозв'язок полярних та декартових координат на прикладі конкретної точки. Розглянемо прямокутний трикутник, в якому гіпотенуза дорівнює полярному радіусу: , а катети – «іксової» та «ігрекової» координат точки в декартовій системі координат: .

Синус гострого кута – є відношення протилежного катета до гіпотенузи:

Косинус гострого кута – є ставлення прилеглого катетадо гіпотенузи:

Заодно повторили визначення синуса, косинуса (і трохи раніше тангенсу) із програми 9 класу загальноосвітньої школи.

Будь ласка, занесіть у свій довідник робочі формули, що виражають декартові координати точки через її полярні координати – з ними нам доведеться зіткнутися ще неодноразово, і в Наступного разупрямо зараз =)

Знайдемо координати точки у прямокутній системі координат:

Таким чином:

Отримані формули відкривають ще одну лазівку в задачі побудови, коли можна обійтися взагалі без транспорту: спочатку знаходимо декартові координати точки (зрозуміло, на чернетці), потім подумки знаходимо потрібне місцена кресленні та відзначаємо дану точку. на заключному етапіпроводимо тонку пряму, яка проходить через побудовану точку та полюс. В результаті виходить, що кут буцімто був відміряний транспортиром.

Забавно, що зовсім відчайдушні студенти можуть обійтися навіть без лінійки, використовуючи замість неї рівний край підручника, зошита або залікової книжки – адже про метрику подбали виробники зошитів, 1 клітинка = 5 міліметрів.

Нагадало мені все це відомий анекдот, в якому винахідливі льотчики прокладали курс по пачці Біломора =) Хоча, жарти жартами, а анекдот не так далекий від реальності, пригадується, на одному з внутрішніх рейсів по РФ у лайнері відмовили всі навігаційні прилади, і екіпаж успішно посадив борт за допомогою звичайної склянки з водою, яка показувала кут нахилу літака щодо землі. А льотна смуга - ось вона, з лобового скла видно.

Використовуючи процитовану на початку уроку теорему Піфагора, легко отримати і зворотні формули: , отже:

Сам кут «фі» стандартно виражається через арктангенс – так само як і аргумент комплексного числаз усіма його заморочками.

Другу групу формул також доцільно помістити у свій довідковий багаж.

Після детального розборупольотів з окремими точками перейдемо до закономірного продовження теми:

Рівняння лінії у полярних координатах

По суті, рівняння лінії в полярній системі координат є функцію полярного радіусу від полярного кута (аргументу). При цьому полярний кут враховується у радіанах(!) І безперервноприймає значення від до (іноді слід розглянути до нескінченності, або ж у ряді завдань для зручності від до). Кожному значенню кута «фі», що входить до область визначенняфункції, відповідає єдине значенняполярний радіус.

Полярну функцію можна порівняти зі своєрідним радаром - коли промінь світла, що виходить з полюса, обертається проти годинникової стрілки і виявляє (промальовує) лінію.

Черговим прикладом полярної кривої є Архімедова спіраль. На наступному малюнку зображено її перший виток– коли полярний радіус слідом за полярним кутом набуває значення від 0 до :

Далі, перетинаючи полярну вісь у точці, спіраль продовжить розкручуватися, нескінченно далеко віддаляючись від полюса. Але подібні випадки практично зустрічаються досить рідко; більше типова ситуаціяколи на всіх наступних оборотах ми «пройдемося по тій самій лінії», яка отримана в діапазоні .

У першому прикладі ми стикаємося і з поняттям області визначенняполярної функції: оскільки полярний радіус невід'ємний, то негативні кути тут розглядати не можна.

! Примітка : у ряді випадків прийнято використовувати узагальнені полярні координатиде радіус може бути негативним, і такий підхід ми коротко вивчимо трохи пізніше

Крім спіралі Архімеда, є безліч інших відомих кривих, але мистецтвом, як то кажуть, ситий не будеш, тому я підібрав приклади, які дуже часто зустрічаються в реальних практичних завданнях.

Спочатку найпростіші рівняння та найпростіші лінії:

Рівняння виду задає вихідний із полюса промінь. Дійсно, вдумайтеся, якщо значення кута завжди(Яким би не було «ер») постійно, то яка це лінія?

Примітка : в узагальненій полярній системі координат дане рівняннязадає пряму, що проходить через полюс

Рівняння виду визначає… здогадайтеся з першого разу – якщо для будь-когокута "фі" радіус залишається постійним? Фактично це визначення колаз центром у полюсі радіуса.

Наприклад, . Для наочності знайдемо рівняння цієї лінії у прямокутній системі координат. Використовуючи отриману в попередньому параграфі формулу, проведемо заміну:

Зведемо обидві частини квадрат:

– рівняння колаз центром на початку координат радіуса 2, що потрібно перевірити.

З часів створення та релізу статті про лінійну залежність та лінійну незалежність векторівя отримав кілька листів від відвідувачів сайту, які ставили питання на кшталт: «ось є проста і зручна прямокутна система координат, навіщо потрібен ще якийсь косокутний афінний випадок?». Відповідь проста: математика прагне охопити все і вся! Крім того, у тій чи іншій ситуації важлива зручність – як бачите, з колом значно вигідніше працювати саме в полярних координатах через граничну простоту рівняння.

А інколи математична модельпередбачає наукові відкриття. Так, свого часу ректор Казанського університету Н.І. Лобачевський суворо довів, через довільну точку площини можна провести нескінченно багато прямих, паралельних даній. В результаті він був ошельмований всім науковим світом, але… спростувати даний фактніхто не зміг. Тільки через добре століття астрономи з'ясували, що світло в космосі поширюється кривими траєкторіями, де і починає працювати неевклідова геометрія Лобачевського, формально розроблена ним задовго до цього відкриття. Передбачається, що це властивість самого простору, кривизна якого нам непомітна через малі (за астрономічними мірками) відстані.

Розглянемо найзмістовніші завдання на побудову:

Приклад 2

Побудувати лінію

Рішення: в першу чергу знайдемо область визначення. Так як полярний радіус невід'ємний, то має виконуватися нерівність. Можна згадати шкільні правиларозв'язання тригонометричних нерівностей, але в простих випадкахяк цей, я раджу швидший та наочний методрішення:

Подайте графік косинуса. Якщо він ще не встиг відкластися в пам'яті, знайдіть його на сторінці Графіки елементарних функцій. Про що нам повідомляє нерівність? Воно повідомляє нам про те, що графік косинуса повинен розташовуватися не нижчеосі абсцис. А це відбувається на відрізку. І відповідно інтервал не підходить.

Таким чином, область визначення нашої функції: тобто графік розташований праворуч від полюса (за термінологією декартової системи – у правій напівплощині).

У полярних координатах часто буває невиразне уявлення про те, яку лінію визначає те чи інше рівняння, тому щоб її побудувати, необхідно знайти належні їй точки - і чим більше, тим краще. Зазвичай обмежуються десятком-другим (а то й меншою кількістю). Найпростіше, звичайно ж, взяти табличні значення кута. Для більшої ясності до негативним значеннямя «прикручуватиму» один оборот:

Через парність косинуса відповідні позитивні значенняможна заново не рахувати:

Зобразимо полярну систему координат і відкладемо знайдені точки, у своїй однакові значення"ер" зручно відкладати за один раз, роблячи парні засічки циркулем за розглянутою вище технологією:

В принципі, лінія виразно промальовується, але щоб повністю підтвердити гіпотезу, давайте знайдемо її рівняння в декартовій системі координат. Можна застосувати нещодавно виведені формули але я розповім вам про більш хитрий прийом. Обидві частини рівняння штучно домножуємо на «ер»: і використовуємо компактніші формули переходу:

Виділяючи повний квадрат, наводимо рівняння лінії до впізнаваного вигляду:

– рівняння колаз центром у точці, радіуса 2.

Якщо за умовою потрібно було просто виконати побудову і все, плавно з'єднуємо знайдені точки лінією:

Готово. Нічого страшного, якщо вийде трохи нерівно, ви ж не повинні були знати, що це коло;-)

Чому ми не розглянули значення кута поза проміжком? Відповідь проста: немає сенсу. Через періодичність функції нас чекає нескінченний біг по побудованому колу.

Нескладно провести нехитрий аналіз і зробити висновок, що рівняння виду задає коло діаметра з центром у точці . Образно кажучи, всі такі кола сидять на полярній осі і обов'язково проходять через полюс. Якщо ж, то весела компаніяперекочує ліворуч - на продовження полярної осі (подумайте, чому).

Схоже завдання для самостійного рішення:

Приклад 3

Побудувати лінію та знайти її рівняння у прямокутній системі координат.

Систематизуємо порядок розв'язання задачі:

Насамперед знаходимо область визначення функції, для цього зручно подивитися на синусоїдущоб відразу ж зрозуміти, де синус невід'ємний.

На другому кроці розраховуємо полярні координати точок, використовуючи табличні значення кутів; проаналізуйте, чи не можна скоротити кількість обчислень?

На третьому етапі відкладаємо точки в полярній системі координат і акуратно з'єднуємо їх лінією.

І, нарешті, знаходимо рівняння лінії декартової системі координат.

Зразковий зразок рішення наприкінці уроку.

Загальний алгоритм та техніку побудови в полярних координатах ми деталізуємо
і суттєво прискоримоу другій частині лекції, але перед цим познайомимося ще з однією поширеною лінією:

Полярна троянда

Правильно, мова піде про квітку з пелюстками:

Приклад 4

Побудувати лінії, задані рівняннями у полярних координатах

Існує два підходи до побудови полярної троянди. Спочатку підемо по накатаній колії, вважаючи, що полярний радіус не може бути негативним:

Рішення:

а) Знайдемо область визначення функції:

Таке тригонометрична нерівністьтеж неважко вирішити графічно: із матеріалів статті Геометричні перетворення графіківВідомо, що й аргумент функції подвоїти, її графік стиснеться до осі ординат вдвічі. Будь ласка, знайдіть графік функції в першому прикладі зазначеного уроку. Де ця синусоїда знаходиться вище осі абсцис? На інтервалах . Отже, нерівності задовольняють відповідні відрізки, та область визначеннянашої функції: .

Взагалі, рішення розглянутих нерівностей є об'єднання нескінченної кількості відрізків, але, повторюся, нас цікавить лише один період.

Можливо, деяким читачам легшим здасться аналітичний спосібзнаходження області визначення умовно назву його «нарізка круглого пирога». Різати будемо на рівні частиниі, перш за все, знайдемо межі першого шматка. Розмірковуємо наступним чином: синус невід'ємний, коли його аргумент знаходиться в межах від 0 до рад. включно. У прикладі: . Розділивши всі частини подвійної нерівностіна 2, отримуємо шуканий проміжок:

Тепер починаємо послідовно «нарізати рівні шматки по 90 градусів» проти годинникової стрілки:

– знайдений відрізок , зрозуміло, входить у область визначення;

- Наступний інтервал - не входить;

- Наступний відрізок - входить;

- І, нарешті, інтервал - не входить.

Прямо, як по ромашці - «любить, не любить, любить, не любить» =) З тією відмінністю, що тут не гадання. Так, прямо якесь кохання по-китайськи виходить….

Отже, і лінія є троянду з двома однаковими пелюстками. Креслення цілком допустимо виконати схематично, проте вкрай бажано правильно знайти та відзначити вершини пелюсток. Вершинам відповідають середини відрізків області визначення, які в даному прикладімають очевидні кутові координати . При цьому довжини пелюстокскладають:

Ось закономірний результат дбайливого садівника:

Слід зазначити, що довжину пелюстки легко відразу побачити з рівняння – оскільки синус обмежений: , то максимальне значення«ер» свідомо не перевершить двох.

б) Побудуємо лінію, задану рівнянням. Очевидно, що довжина пелюстки цієї троянди теж дорівнює двом, але, перш за все, нас цікавить область визначення. Застосуємо аналітичний метод«нарізки»: синус невід'ємний, коли його аргументзнаходиться в межах від нуля до «пі» включно, даному випадку: . Ділимо всі частини нерівності на 3 і отримуємо перший проміжок:

Далі починаємо "нарізку пирога шматкам" по рад. (60 градусів):
- Відрізок увійде в область визначення;
– інтервал – не увійде;
- Відрізок - увійде;
– інтервал – не увійде;
- Відрізок - увійде;
- Інтервал - не увійде.

Процес успішно завершено на позначці 360 градусів.

Таким чином, область визначення: .

Проведені події повністю чи частково нескладно здійснювати і подумки.

Побудова. Якщо в попередньому пункті все благополучно обійшлося прямими кутами та кутами в 45 градусів, то тут доведеться трохи повозитися. Знайдемо вершини пелюсток. Їх довжина була видна від початку завдання, залишилося обчислити кутові координати, які дорівнюють серединам відрізків області визначення:

Зверніть увагу, що між вершинами пелюсток повинні обов'язково вийти рівні проміжки, у разі 120 градусів.

Креслення бажано розмітити на 60-градусні сектори (відмежовані зеленими лініями) та провести напрямки вершин пелюсток (сірі лінії). Самі вершини зручно намітити за допомогою циркуля – один раз відміряти відстань у 2 одиниці та нанести три засічки на прокреслених напрямках у 30, 150 та 270 градусів:

Готово. Розумію, що заняття клопітне, але якщо хочете все оформити за розумом, то доведеться витратити час.

Сформулюємо загальну формулу : рівняння виду, – натуральне число), задає полярну-пелюсткову троянду, довжина пелюстки якої дорівнює.

Наприклад, рівняння задає чотирилисток з довжиною пелюстки 5 одиниць, рівняння – 5-пелюсткову троянду з довжиною пелюстки 3 од. і т.д.

Інструкція

Записуйте математичні операціїу текстовому вигляді та вводьте їх у поле пошукового запиту на головній сторінцісайту Google, якщо ви не можете використовувати калькулятор, але маєте доступ в інтернет. Ця пошукова система має вбудований багатофункціональний калькулятор, користуватися яким набагато простіше, ніж будь-яким іншим. Тут немає інтерфейсу з кнопками – вводити всі дані треба в текстовому вигляді в єдине поле. Наприклад, якщо відомі координати крайніх точок відрізкав тривимірної системикоординат A(51,34 17,2 13,02) та A(-11,82 7,46 33,5), то координатисередньої точки відрізка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводячи в поле пошукового запиту (51,34-11,82)/2, потім (17,2+7,46)/2 та (13,02+33,5)/2, можна за допомогою Google отримати координатиЗ(19,76 12,33 23,26).

Стандартне рівняння кола дозволяє дізнатися кілька важливих відомостей про цю фігуру, наприклад, координати її центру, довжину радіуса. У деяких завданнях, навпаки, за заданими параметрами потрібно скласти рівняння.

Інструкція

Визначте, відомості про коло ви маєте, виходячи з даної вам задачі. Запам'ятайте, що кінцевою метоює необхідність визначити координати центру, і навіть діаметр. Усі ваші дії мають бути спрямовані на досягнення саме цього результату.

Використовуйте дані щодо наявності точок перетину з координатними прямими або іншими прямими. Зверніть увагу, що якщо коло проходить через вісь абсцис, друга матиме координату 0, а якщо через вісь ординат – то перша. Ці координати дозволять знайти координати центру кола, а також обчислити радіус.

Не забувайте про основних властивостяхсікних та дотичних. Зокрема, найбільш корисною виявляється теорема про те, що в точці торкання радіус і дотична утворюють прямий кут. Але зверніть увагу, що вас можуть попросити довести всі використані в ході теореми.

Вирішуйте найбільш стандартні типи, щоб навчитися відразу бачити, як використовувати ті чи інші дані для рівняння кола. Так, крім уже зазначених завданьз прямо заданими координатамиі тими, в умовах яких дані відомості про наявність точок перетину, для складання рівняння кола можна скористатися знаннями про центр кола, довжину хорди і , на якій ця хорда лежить.

Для вирішення збудуйте рівнобедрений трикутник, основою якого буде дана хорда, а рівні сторони- Радіусами. Складіть , з якої легко знайдете необхідні дані. Для цього достатньо скористатися формулою для знаходження довжини відрізка у площині.

Відео на тему

Під колом розуміють фігуру, що складається з безлічі точок площини, що рівно віддалені від її центру. Відстань від центру до точок коланазивається радіусом.

Прямокутна система координат на площині утворюється двома взаємно перпендикулярними осямикоординат X'X та Y'Y. Осі координат перетинаються в точці O, яка називається початком координат , на кожній осі вибрано позитивний напрямок. напрямом осі Y'Y. Чотири кути (I, II, III, IV), утворені осями координат X'X та Y'Y, називаються координатними кутами (див. рис. 1).

Положення точки A на площині визначається двома координатами x та y. Координата x дорівнює довжині відрізка OB, координата y - довжині відрізка OC у вибраних одиницях виміру. Відрізки OB і OC визначаються лініями, проведеними з точки A паралельно до осей Y'Y і X'X відповідно. Координата x називається абсцисою точки A, координата y – ординатою точки A. Записують так: A(x, y).

Якщо точка A лежить у координатному вугіллі I, то точка A має позитивні абсцису та ординату. Якщо точка A лежить у координатному вугіллі II, то точка A має негативну абсцису та позитивну ординату. Якщо точка A лежить у координатному вугіллі IIIточка A має негативні абсцису і ординату. Якщо точка A лежить у координатному куті IV, то точка A має позитивну абсцису та негативну ординату.

Прямокутна система координат у просторіутворюється трьома взаємно перпендикулярними осями координат OX, OY та OZ. Осі координат перетинаються в точці O, яка називається початком координат, на кожній осі вибрано позитивний напрямок, вказаний стрілками, і одиниця виміру відрізків на осях. Одиниці виміру однакові всім осей. OX – вісь абсцис, OY – вісь ординат, OZ – вісь аплікат. Позитивний напрямок осей вибирають так, щоб при повороті осі OX проти годинникової стрілки на 90° її позитивний напрямок збіглося з позитивним напрямом осі OY, якщо цей поворот спостерігати з боку позитивного напрямку осі OZ. Така система координат називається правою. Якщо великий палець правої рукиприйняти за напрямок X, вказівний за напрямок Y, а середній за напрямок Z, то утворюється права система координат. Аналогічними пальцями лівої руки утворюється ліва система координат. Праву та ліву системи координат неможливо поєднати так, щоб збіглися відповідні осі (див. мал. 2).

Положення точки A у просторі визначається трьома координатами x, y та z. Координата x дорівнює довжині відрізка OB, координата y – довжині відрізка OC, координата z – довжині відрізка OD у вибраних одиницях вимірювання. Відрізки OB, OC і OD визначаються площинами, проведеними з точки A паралельно площин YOZ, XOZ і XOY відповідно. Координата x називається абсцисою точки A, координата y - ординатою точки A, координата z - аплікати точки A. Записують так: A(a, b, c).

Орти

Прямокутна система координат (будь-який розмірності) також описується набором ортів, сонаправленных з осями координат. Кількість ортів дорівнює розмірності системи координат і вони перпендикулярні одне одному.

У тривимірному випадку такі орти зазвичай позначаються i j kабо e x e y e z. При цьому у разі правої системи координат дійсні такі формули з векторним добутком векторів:

• [i j]=k ;
• [j k]=i ;
• [k i]=j .

Історія

Вперше прямокутну систему координат ввів Рене Декарт у своїй роботі «Міркування про метод» у 1637 році. Тому прямокутну систему координат називають також - Декартова системакоординат. Координатний метод опису геометричних об'єктівзапочаткував аналітичної геометрії. Внесок у розвиток координатного методу вніс також П'єр Ферма, проте його роботи вперше було опубліковано вже після його смерті. Декарт та Ферма застосовували координатний метод лише на площині.

Координатний метод для тривимірного просторувперше застосував Леонард Ейлер вже у XVIII столітті.

Див. також

Посилання

Wikimedia Foundation. 2010 .

• Декартова система координат
• Декартова ступінь

Дивитись що таке "Декартові координати" в інших словниках:

ДЕКАРТОВИ КООРДИНАТИ- (Декартова система координат) система координат на площині або в просторі, зазвичай з взаємно перпендикулярними осями та однаковими масштабами по осях прямокутні декартові координати. Названі на ім'я Р. Декарта … Великий Енциклопедичний словник

декартові координати- Система координат, що складається із двох перпендикулярних осей. Положення точки в такій системі формується за допомогою двох чисел, що визначають відстань від центру координат кожної з осей. Тематики інформаційні. Довідник технічного перекладача

декартові координати- (Декартова система координат), система координат на площині або в просторі, зазвичай з взаємно перпендикулярними осями та однаковими масштабами по осях прямокутні декартові координати. Названі на ім'я Р. Декарта … Енциклопедичний словник

декартові координати- Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: англ. Cartesian coordinates vok. kartesische Koordinaten, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas

декартові координати- Dekarto koordinatės statusas T sritis fizika atitikmenys: angl. Cartesian coordinates; grid coordinates vok. kartesische Koordinaten, f rus. декартові координати f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas

ДЕКАРТОВИ КООРДИНАТИ- спосіб визначення положення точок на площині відстанями до двох фіксованих перпендикулярних прямих осей. Це поняття вбачається вже в Архімеда та Апологія Пергського понад дві тисячі років тому і навіть у стародавніх єгиптян. Вперше ця… Математична енциклопедія

ДЕКАРТОВИ КООРДИНАТИ- Декартова система координат [на ім'я франц. філософа та математика Р. Декарта (R. Descartes; 1596 1650)], система координат на площині або в просторі, зазвичай з взаємно перпендикулярними осями та однаковими масштабами по осях прямокутні Д... Великий енциклопедичний політехнічний словник

ДЕКАРТОВИ КООРДИНАТИ- (Декартова система координат), система координат на площині або в просторі, зазвичай з взаємно перпендикулярними осями та однаковими масштабами по осях прямокутні Д. до. Названі на ім'я Р. Декарта … Природознавство. Енциклопедичний словник

ДЕКАРТОВИ КООРДИНАТИ- Система розташування будь-якої точки знайшли кістки щодо двох осей, що перехрещуються під прямим кутом. Розроблена Рене Декартом ця система стала основою для стандартних методів графічного уявленняданих. Горизонтальна лінія. Тлумачний словникз психології

Координати- Координати. На площині (ліворуч) та у просторі (праворуч). КООРДИНАТИ (від латинського co спільно і ordinatus впорядкований), числа, які визначають положення точки на прямій, площині, поверхні, у просторі. Координати суть відстані … Ілюстрований енциклопедичний словник