Зворотна функція логарифму. Формули логарифмів

Випливають із його визначення. І так логарифм числа bна підставі авизначається як показник ступеня, в який треба звести число a, щоб отримати число b(Логарифм існує тільки у позитивних чисел).

З цього формулювання випливає, що обчислення x=log a b, рівнозначне рішенню рівняння a x = b.Наприклад, log 2 8 = 3тому що 8 = 2 3 . Формулювання логарифму дає можливість довести, що якщо b=a з, то логарифм числа bна підставі aдорівнює з. Також ясно, що тема логарифмування тісно пов'язана з темою ступеня числа .

З логарифмами, як і з будь-якими числами, можна виконувати операції складання, відніманняі всіляко трансформувати. Але через те, що логарифми - це не зовсім ординарні числа, тут застосовні свої особливі правила, які називаються основними властивостями.

Складання та віднімання логарифмів.

Візьмемо два логарифми з однаковими підставами: log a xі log a y. Тоді зними можна виконувати операції складання та віднімання:

log a x + log a y = log a (x · y);

log a x - log a y = log a (x: y).

log a(x 1 . x 2 . x 3 ... x k) = log a x 1 + log a x 2 + log a x 3 + ... + log a x k.

З теореми логарифму приватногоможна отримати ще одну властивість логарифму. Загальновідомо, що log a 1= 0, отже,

log a 1 /b= log a 1 - log a b= - log a b.

А значить має місце рівність:

log a 1 / b = - log a b.

Логарифми двох взаємно зворотних чисел по одному й тому підставі будуть різні друг від друга виключно знаком. Так:

Log 3 9 = - log 3 1/9; log 5 1/125 = -log 5 125.

Логарифмом числа N на підставі а називається показник ступеня х , в яку потрібно звести а , щоб отримати число N

За умови, що
,
,

З визначення логарифму випливає, що
, тобто.
- ця рівність є основною логарифмічною тотожністю.

Логарифми на підставі 10 називаються десятковими логарифмами. Замість
пишуть
.

Логарифми на підставі e називаються натуральними та позначаються
.

Основні властивостілогарифмів.

Логарифм одиниці за будь-якої підстави дорівнює нулю

Логарифм твору дорівнює сумілогарифмів співмножників.

3) Логарифм приватного дорівнює різницілогарифмів

Множник
називається модулем переходу від логарифмів на підставі a до логарифмів на підставі b .

За допомогою властивостей 2-5 часто вдається звести логарифм складного виразу результату простих арифметичних дій над логарифмами.

Наприклад,

Такі перетворення логарифму називаються логарифмуванням. Перетворення зворотні логарифмування називаються потенціюванням.

Розділ 2. Елементи вищої математики.

1. Межі

Межею функції
є кінцеве число А, якщо при прагненні xx 0 для кожного наперед заданого
, знайдеться таке число
, що як тільки
, то
.

Функція, що має межу, відрізняється від нього на нескінченно малу величину:
, де -б.м.в., тобто.
.

приклад. Розглянемо функцію
.

При прагненні
, функція y прагне до нуля:

1.1. Основні теореми про межі.

Межа постійної величинидорівнює цій постійній величині

Межа суми (різниці) кінцевого числафункцій дорівнює сумі (різниці) меж цих функций.

Межа добутку кінцевого числа функцій дорівнює творумеж цих функций.

Межа частки двох функцій дорівнює приватній межі цих функцій, якщо межа знаменника не дорівнює нулю.

Чудові межі

,
, де

1.2. Приклади обчислення меж

Однак не всі межі обчислюються так просто. Найчастіше обчислення межі зводиться до розкриття невизначеності типу: або .

2. Похідна функції

Нехай ми маємо функцію
, безперервну на відрізку
.

Аргумент отримав деякий приріст
. Тоді і функція отримає збільшення
.

Значення аргументу відповідає значення функції
.

Значення аргументу
відповідає значення функції.

Отже, .

Знайдемо межу цього відношення при
. Якщо ця межа існує, то вона називається похідною цієї функції.

Визначення 3Виробної даної функції
за аргументом називається межа відношення збільшення функції до збільшення аргументу, коли збільшення аргументу довільним чином прагне до нуля.

Похідна функції
може бути позначена таким чином:

; ; ; .

Визначення 4Операція знаходження похідної від функції називається диференціюванням.

2.1. Механічний сенс похідної.

Розглянемо прямолінійний рух деякого твердого тіла чи матеріальної точки.

Нехай у певний момент часу точка, що рухається
знаходилась на відстані від початкового становища
.

Через деякий проміжок часу
вона перемістилася на відстань
. Ставлення =- Середня швидкістьматеріальної точки
. Знайдемо межу цього відношення, враховуючи що
.

Отже, визначення миттєвої швидкостірух матеріальної точки зводиться до знаходження похідної від шляху за часом.

2.2. Геометричне значенняпохідний

Нехай ми маємо графічно задану деяку функцію
.

Мал. 1. Геометричний зміст похідної

Якщо
, то крапка
, буде переміщатися кривою, наближаючись до точки
.

Отже
, тобто. значення похідної за даного значення аргументу чисельно дорівнює тангенсу кута утвореного дотичної в даній точці з позитивним напрямом осі
.

2.3. Таблиця основних формул диференціювання.

Ступінна функція

Показова функція

Логарифмічна функція

Тригонометрична функція

Зворотна тригонометрична функція

2.4. Правила диференціювання.

Похідна від

Похідна суми (різниці) функцій

Похідна робота двох функцій

Похідна приватного двох функцій

2.5. Похідна від складної функції.

Нехай дана функція
така, що її можна подати у вигляді

і
, де змінна є проміжним аргументом, тоді

Похідна складної функції дорівнює добутку похідної цієї функції за проміжним аргументом на похідну проміжного аргументу по x.

Приклад1.

Приклад2.

3. Диференціал функції.

Нехай є
, що диференціюється на деякому відрізку
і нехай у цієї функції є похідна

тоді можна записати

(1),

де - нескінченно мала величина,

так як при

Помножуючи всі члени рівності (1) на
маємо:

Де
- Б.М.В. вищого ладу.

Величина
називається диференціалом функції
і позначається

3.1. Геометричне значення диференціалу.

Нехай дана функція
.

Рис.2. Геометричний зміст диференціала.

Очевидно, що диференціал функції
дорівнює приросту ординати дотичної в цій точці.

3.2. Похідні та диференціали різних порядків.

Якщо є
тоді
називається першою похідною.

Похідна від першої похідної називається похідною другого порядку та записується
.

Похідний n-го порядку від функції
називається похідна (n-1)-го порядку та записується:

Диференціал від диференціалу функції називається другим диференціалом чи диференціалом другого порядку.

.

.

3.3 Розв'язання біологічних завдань із застосуванням диференціювання.

Задача1. Дослідження показали, що зростання колонії мікроорганізмів підпорядковується закону
, де N – чисельність мікроорганізмів (у тис.), t -Час (Дні).

б) Чи буде в цей період чисельність колонії збільшуватися чи зменшуватись?

Відповідь. Чисельність колонії збільшуватиметься.

Задача 2. Вода в озері періодично тестується контролю вмісту хвороботворних бактерій. Через t днів після тестування концентрація бактерій визначається співвідношенням

Коли в озері настане мінімальна концентрація бактерій і чи можна буде в ньому купатися?

РішенняФункція досягає max або min, коли її похідна дорівнює нулю.

Визначимо max чи min буде через 6 днів. Для цього візьмемо другу похідну.

Відповідь: Через 6 днів буде мінімальна концентрація бактерій.

Дотримання Вашої конфіденційності є важливим для нас. З цієї причини ми розробили Політику конфіденційності, яка описує, як ми використовуємо та зберігаємо Вашу інформацію. Будь ласка, ознайомтеся з нашими правилами дотримання конфіденційності та повідомте нам, якщо у вас виникнуть будь-які питання.

Збір та використання персональної інформації

Під персональної інформацією розуміються дані, які можна використовувати для ідентифікації певного особи чи зв'язку з ним.

Від вас може бути запрошено надання вашої персональної інформації у будь-який момент, коли ви зв'язуєтесь з нами.

Нижче наведено приклади типів персональної інформації, яку ми можемо збирати, і як ми можемо використовувати таку інформацію.

Яку персональну інформацію ми збираємо:

Коли ви залишаєте заявку на сайті, ми можемо збирати різну інформацію, включаючи ваше ім'я, номер телефону, адресу електронної поштиі т.д.

Як ми використовуємо вашу персональну інформацію:

Збирається нами Персональна інформаціядозволяє нам зв'язуватися з вами та повідомляти про унікальних пропозиціях, акціях та інших заходах та найближчих подіях.
Час від часу ми можемо використовувати вашу персональну інформацію для надсилання важливих повідомлень та повідомлень.
Ми також можемо використовувати персональну інформацію для внутрішніх цілей, таких як проведення аудиту, аналізу даних та різних дослідженьз метою покращення послуг наданих нами та надання Вам рекомендацій щодо наших послуг.
Якщо ви берете участь у розіграші призів, конкурсі або подібному стимулювальному заході, ми можемо використовувати інформацію, що надається, для управління такими програмами.

Розкриття інформації третім особам

Ми не розкриваємо отриману від Вас інформацію третім особам.

Винятки:

Якщо необхідно - відповідно до закону, судовим порядком, у судовому розгляді, та/або на підставі публічних запитів або запитів від державних органівна території РФ – розкрити вашу персональну інформацію. Ми також можемо розкривати інформацію про вас, якщо ми визначимо, що таке розкриття необхідно чи доречно з метою безпеки, підтримання правопорядку, чи інших суспільно важливих випадках.
У разі реорганізації, злиття або продажу ми можемо передати персональну інформацію, що збирається нами, відповідній третій особі – правонаступнику.

Захист персональної інформації

Ми вживаємо запобіжних заходів - включаючи адміністративні, технічні та фізичні - для захисту вашої персональної інформації від втрати, крадіжки та недобросовісного використання, а також від несанкціонованого доступу, розкриття, зміни та знищення.

Дотримання вашої конфіденційності на рівні компанії

Для того, щоб переконатися, що ваша персональна інформація знаходиться в безпеці, ми доводимо норми дотримання конфіденційності та безпеки до наших співробітників і суворо стежимо за дотриманням заходів дотримання конфіденційності.

Визначення логарифму

Логарифмом числа b на підставі а називається показник ступеня, в який потрібно звести а щоб отримати b .

Числом ев математиці прийнято позначати межу, якої прагнути вираз

Число еє ірраціональним числом - Числом, несумірним з одиницею, воно не може бути точно вираженим ні цілим ні дробовим раціональнимчислом.

Літера е- перша буква латинського слова exponere- виставляти напоказ, звідси в математиці назва експоненційна- Показова функція.

Число ешироко застосовується в математиці, і в усіх науках, які так чи інакше застосовують для своїх потреб математичні розрахунки.

Логарифми. Властивості логарифмів

Визначення: Логарифмом позитивного числа b по основі називається показник ступеня с, в яку треба звести число а щоб отримати число b.

Основна логарифмічна тотожність:

7) Формула переходу до нової основи:

lna = log e a, e ≈ 2,718…

Завдання та тести на тему «Логорифми. Властивості логарифмів»

Логарифми - Важливі теми для повторення ЄДІ з математики

Для успішного виконання завдань на цю тему Ви повинні знати визначення логарифму, властивості логарифмів, основну логарифмічну тотожність, визначення десяткового та натурального логарифмів. Основні типи завдань з цієї теми — це завдання на обчислення та перетворення логарифмічних виразів. Розглянемо їхнє рішення на наступні приклади.

Рішення:Використовуючи властивості логарифмів, отримаємо

Рішення:використовуючи властивості ступеня, отримаємо

1) (2 2) log 2 5 = (2 log 2 5) 2 = 5 2 = 25

Властивості логарифмів, формулювання та докази.

Логарифми мають поруч характерних властивостей. У цій статті ми розберемо основні властивості логарифмів. Тут ми дамо їх формулювання, запишемо властивості логарифмів як формул, покажемо приклади їх застосування, і навіть наведемо докази властивостей логарифмів.

Навігація на сторінці.

Основні властивості логарифмів, формули

Для зручності запам'ятовування та використання уявимо основні властивості логарифмівяк списку формул. У наступному пунктідамо їх формулювання, докази, приклади використання та необхідні пояснення.

Властивість логарифму одиниці: log a 1=0 будь-якого a>0 , a≠1 .

Логарифм числа, рівної основи: log a a=1 при a>0 , a≠1 .

Властивість логарифму ступеня основи: log a a p =p , де a>0 , a≠1 та p – будь-яке дійсне число.

Логарифм добутку двох позитивних чисел: log a (x · y) = log a x + log a y , a>0 , a≠1 , x>0 , y>0 ,
і властивість логарифму добутку n позитивних чисел: log a (x 1 · x 2 · ... · x n) = log a x 1 +log a x 2 + ... >0, …, x n >0 .

Властивість приватного логарифму:

, де a>0, a≠1, x>0, y>0.

Логарифм ступеня числа: log a b p = p log a | b | , де a>0 , a≠1 , b та p такі числа, що ступінь b p має сенс і b p >0 .

Наслідок:

, де a>0, a≠1, n – натуральне число, більше одиниці, b>0.

Наслідок 1:

, a>0, a≠1, b>0, b≠1.

Наслідок 2:

, a>0 , a≠1 , b>0 , p і q – дійсні числа, q≠0 , зокрема при b=a маємо

Формулювання та докази властивостей

Переходимо до формулювання та доказу записаних властивостей логарифмів. Всі властивості логарифмів доводяться на основі визначення логарифму і основного логарифмічного тотожності, що випливає з нього, а також властивостей ступеня.

Почнемо зі властивості логарифму одиниці. Його формулювання таке: логарифм одиниці дорівнює нулю, тобто, log a 1=0для будь-якого a>0, a≠1. Доказ не викликає складнощів: оскільки a 0 =1 для будь-якого a , що задовольняє зазначеним вище умовам a>0 і a≠1 , то рівність log a 1=0 відразу випливає з визначення логарифму.

Наведемо приклади застосування розглянутої якості: log 3 1=0 , lg1=0 і .

Переходимо до наступної властивості: логарифм числа, рівного підставі, дорівнює одиниці , тобто, log a a=1при a>0, a≠1. Справді, оскільки a 1 =a для будь-якого a , то визначення логарифму log a a=1 .

Прикладами використання цієї властивості логарифмів є рівності log 5 5 = 1, log 5,6 5,6 і lne = 1 .

Логарифм ступеня числа, що дорівнює підставі логарифму, дорівнює показникуступеня. Цій властивості логарифму відповідає формула виду log a a p = p, де a>0, a≠1 і p – будь-яке дійсне число. Ця властивість безпосередньо випливає з визначення логарифму. Зауважимо, що воно дозволяє відразу вказати значення логарифму, якщо є можливість уявити число під знаком логарифму у вигляді ступеня основи, детальніше про це ми поговоримо у статті обчислення логарифмів.

Наприклад, log 2 2 7 =7 , lg10 -4 =-4 і .

Логарифм твору двох позитивних чисел x і y дорівнює добутку логарифмів цих чисел: log a (x · y) = log a x + log a y, a>0, a≠1. Доведемо властивість логарифму твору. У силу властивостей ступеня a log a x + log a y = a log a x a log a y , а так як по основному логарифмічної тотожності a log a x = x і a log a y = y , то a log a x log a y = x y. Таким чином, a log a x + log a y = x · y, звідки за визначенням логарифму випливає рівність, що доводиться.

Покажемо приклади використання властивості логарифму добутку: log 5 (2·3)=log 5 2+log 5 3 .

Властивість логарифму твору можна узагальнити добуток кінцевого числа n позитивних чисел x 1 , x 2 , …, x n як log a (x 1 · x 2 · ... · x n) = log a x 1 + log a x 2 + ... + log a x n. Ця рівність без проблем доводиться методом математичної індукції.

Наприклад, натуральний логарифм твору можна замінити сумою трьох натуральних логарифмів чисел 4 , e , і .

Логарифм приватного двох позитивних чисел x і y дорівнює різниці логарифмів цих чисел. Властивості приватного логарифму відповідає формула виду , де a>0, a≠1, x та y – деякі позитивні числа. Справедливість цієї формули доводиться як і формула логарифму твору: оскільки , то за визначенням логарифму .

Наведемо приклад використання цієї властивості логарифму: .

Переходимо до властивості логарифму ступеня. Логарифм ступеня дорівнює добутку показника ступеня на логарифм модуля основи цього ступеня. Запишемо цю властивість логарифму ступеня у вигляді формули: log a b p = log a | b |, де a>0 , a≠1 , b та p такі числа, що ступінь b p має сенс і b p >0 .

Спочатку доведемо цю властивість для позитивних b. Основне логарифмічне тотожність дозволяє нам уявити число b як a log a b тоді b p = (a log a b) p , а отримане вираз в силу властивість ступеня дорівнює a p · log a b . Так ми приходимо до рівності b p = a p · log a b , з якого за визначенням логарифму укладаємо, що log a b p = p · log a b .

Залишилося довести цю властивість для негативних b. Тут зауважуємо, що вираз log a b p при негативних b має сенс лише при парних показниках ступеня p (оскільки значення ступеня b p має бути більше нуля, інакше логарифм нічого очікувати мати сенсу), а цьому разі b p =|b| p. Тоді b p = | b | p = (a log a | b |) p = a p · log a | b | , Звідки log a b p = p log a | b | .

Наприклад, і ln(-3) 4 =4·ln|-3|=4·ln3 .

Із попередньої властивості випливає властивість логарифму з кореня: логарифм кореня n -ого ступеня дорівнює добутку дробу 1/n на логарифм підкореного виразу, Тобто, , де a>0, a≠1,n - натуральне число, більше одиниці, b>0.

Доказ базується на рівності (дивіться визначення ступеня з дробовим показником), яке справедливе для будь-яких позитивних b і властивості логарифму ступеня: .

Ось приклад використання цієї властивості: .

Тепер доведемо формулу переходу до нової основи логарифмувиду . Для цього достатньо довести справедливість рівності log c b = log a b log c a . Основне логарифмічне тотожність дозволяє нам число b уявити як a log a b тоді log c b = log c a log a b . Залишилося скористатися властивістю логарифму ступеня: log ca log ab = log ab log ca . Так доведено рівність log c b = log a b log c a , а значить, доведено і формулу переходу до нової основи логарифму .

Покажемо кілька прикладів застосування цієї властивості логарифмів: і .

Формула переходу до нової основи дозволяє переходити до роботи з логарифмами, що мають «зручну» основу. Наприклад, з її допомогою можна перейти до натуральних або десяткових логарифмів, щоб можна було обчислити значення логарифму таблиці логарифмів. Формула переходу до нової основи логарифму також дозволяє в деяких випадках знаходити значення логарифму, коли відомі значення деяких логарифмів з іншими основами.

Часто використовується окремий випадокформули початку нової основи логарифма при c=b виду . Звідси видно, що log ab і log ba – взаємно зворотні числа. Наприклад, .

Також часто використовується формула, яка зручна при знаходженні значень логарифмів. Для підтвердження своїх слів покажемо, як з її допомогою обчислюється значення логарифму . Маємо . Для доказу формули достатньо скористатися формулою переходу до нової основи логарифму: .

Залишилося довести властивості порівняння логарифмів.

Скористаємося методом від неприємного. Припустимо, що за a 1 >1 , a 2 >1 і a 1 2 і за 0 1 справедливо log a 1 b≤log a 2 b . За властивостями логарифмів ці нерівності можна переписати як і відповідно, а з них випливає, що log b a 1 ≤ log b a 2 і log b a 1 ≥ log b a 2 відповідно. Тоді за властивостями ступенів з однаковими основами повинні виконуватися рівності b log b a 1 b log b a 2 і b log b a 1 b log b a 2 , тобто, a 1 a 2 . Так ми дійшли суперечності умові a 1 2 . На цьому доказ завершено.

Основні властивості логарифмів

Матеріали до уроку
Завантажити всі формули

Логарифми, як і будь-які числа, можна складати, віднімати та всіляко перетворювати. Але оскільки логарифми – це не зовсім звичайні числа, тут є свої правила, які називаються основними властивостями.

Ці правила обов'язково треба знати – без них не вирішується жодне серйозне логарифмічне завдання. До того ж їх зовсім небагато - все можна вивчити за один день. Отже, почнемо.

Додавання та віднімання логарифмів

Розглянемо два логарифми з однаковими основами: log a x та log a y . Тоді їх можна складати і віднімати, причому:

Отже, сума логарифмів дорівнює логарифму добутку, а різниця - приватного логарифму. Зверніть увагу: ключовий моменттут - однакові підстави. Якщо підстави різні, ці правила не працюють!

Ці формули допоможуть обчислити логарифмічний виразнавіть тоді, коли окремі його частини не рахуються (див. урок «Що таке логарифм»). Погляньте на приклади – і переконайтесь:

Завдання. Знайдіть значення виразу: log 6 4 + log 6 9.

Оскільки підстави у логарифмів однакові, використовуємо формулу суми:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.

Завдання. Знайдіть значення виразу: log 2 48 − log 2 3.

Підстави однакові, використовуємо формулу різниці:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Завдання. Знайдіть значення виразу: log 3 135 − log 3 5.

Знову підстави однакові, тому маємо:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Як бачите, вихідні вирази складені з поганих логарифмів, які окремо не вважаються. Але після перетворень виходять цілком нормальні числа. На цьому факті побудовано багато контрольні роботи. Та що контрольні - подібні висловлюванняна повному серйозі (іноді - практично без змін) пропонуються на ЄДІ.

Винесення показника ступеня з логарифму

Тепер трохи ускладнимо завдання. Що, якщо у підставі чи аргументі логарифма стоїть ступінь? Тоді показник цього ступеня можна винести за знак логарифму за такими правилами:

log a x n = n · log a x;

Неважко помітити, що останнє правилослід їх перших двох. Але краще його все ж таки пам'ятати - в деяких випадках це значно скоротить обсяг обчислень.

Зрозуміло, всі ці правила мають сенс при дотриманні ОДЗлогарифма: a > 0, a ≠ 1, x > 0. І ще: вчіться застосовувати всі формули як зліва направо, а й навпаки, тобто. можна вносити числа, що стоять перед знаком логарифму, до самого логарифму. Саме це найчастіше й потрібне.

Завдання. Знайдіть значення виразу: log 7 49 6 .

Позбавимося ступеня в аргументі за першою формулою:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12

Завдання. Знайдіть значення виразу:

[Підпис до малюнка]

Зауважимо, що у знаменнику стоїть логарифм, основа та аргумент якого є точними ступенями: 16 = 2 4 ; 49 = 7 2 . Маємо:

[Підпис до малюнка]

Думаю, до останньому прикладупотрібні пояснення. Куди зникли логарифми? До останнього моменту ми працюємо лише зі знаменником. Представили підставу і аргумент логарифму, що там стоїть, у вигляді ступенів і винесли показники - отримали «триповерховий» дріб.

Тепер подивимося на основний дріб. У чисельнику і знаменнику стоїть те саме число: log 2 7. Оскільки log 2 7 ≠ 0, можемо скоротити дріб - у знаменнику залишиться 2/4. За правилами арифметики, четвірку можна перенести в чисельник, що було зроблено. В результаті вийшла відповідь: 2.

Перехід до нової основи

Говорячи про правила складання та віднімання логарифмів, я спеціально підкреслював, що вони працюють лише за однакових підстав. А що, коли підстави різні? Що, якщо вони не є точними ступенями того самого числа?

На допомогу приходять формули переходу до нової основи. Сформулюємо їх як теореми:

Нехай даний логарифм log a x. Тоді для будь-якого числа c такого, що c > 0 і c ≠ 1, правильна рівність:

[Підпис до малюнка]

Зокрема, якщо покласти c = x, отримаємо:

[Підпис до малюнка]

З другої формули випливає, що можна міняти місцями основу та аргумент логарифму, але при цьому весь вислів «перевертається», тобто. логарифм опиняється у знаменнику.

Ці формули рідко зустрічаються у звичайних числових виразів. Оцінити, наскільки вони зручні, можна лише за рішенням логарифмічних рівняньта нерівностей.

Втім, існують завдання, які взагалі не вирішуються інакше як переходом до нової основи. Розглянемо пару таких:

Завдання. Знайдіть значення виразу: log 5 16 · log 2 25.

Зауважимо, що в аргументах обох логарифмів стоять точні ступені. Винесемо показники: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

А тепер «перевернемо» другий логарифм:

[Підпис до малюнка]

Оскільки від перестановки множників твір не змінюється, ми спокійно перемножили четвірку та двійку, а потім розібралися з логарифмами.

Завдання. Знайдіть значення виразу: log 9 100 · lg 3.

Підстава та аргумент першого логарифму – точні ступені. Запишемо це і позбудемося показників:

[Підпис до малюнка]

Тепер позбудемося десяткового логарифму, перейшовши до нової основи:

[Підпис до малюнка]

Основне логарифмічне тотожність

Часто в процесі рішення потрібно представити число як логарифм на задану основу. У цьому випадку нам допоможуть формули:

n = log a a n
У першому випадку число n стає показником ступеня, що стоїть у аргументі. Число n може бути абсолютно будь-яким, адже це просто значення логарифму.

Друга формула – це фактично перефразоване визначення. Вона так і називається: основна логарифмічна тотожність.

Справді, що буде, якщо число b звести на такий ступінь, що число b у цій мірі дає число a ? Правильно: вийде це число a . Уважно прочитайте цей абзац ще раз – багато хто на ньому «зависає».

Подібно до формул переходу до нової основи, основна логарифмічна тотожність іноді буває єдино можливим рішенням.

[Підпис до малюнка]

Зауважимо, що log 25 64 = log 5 8 - просто винесли квадрат із підстави та аргументу логарифму. Враховуючи правила множення ступенів з однаковою основою, отримуємо:

[Підпис до малюнка]

Якщо хтось не в курсі, це було справжнє завдання з ЄДІ 🙂

Логарифмічна одиниця та логарифмічний нуль

Насамкінець наведу дві тотожності, які складно назвати властивостями - швидше, це наслідки з визначення логарифму. Вони постійно зустрічаються у завданнях і, що дивно, створюють проблеми навіть для «просунутих» учнів.
1. log a a = 1 – це логарифмічна одиниця. Запам'ятайте раз і назавжди: логарифм з будь-якої основи a від самої цієї основи дорівнює одиниці.
2. log a 1 = 0 – це логарифмічний нуль. Підстава a може бути будь-яким, але якщо в аргументі стоїть одиниця - логарифм дорівнює нулю! Тому що a 0 = 1 – це прямий слідствоіз визначення.
Ось і всі властивості. Обов'язково потренуйтеся застосовувати їх на практиці! Завантажте шпаргалку на початку уроку, роздрукуйте її – і вирішуйте завдання.

Логарифм. Властивості логарифму (складання та віднімання).

Властивості логарифмувипливають із його визначення. І так логарифм числа bна підставі авизначається як показник ступеня, в який треба звести число a, щоб отримати число b(Логарифм існує тільки у позитивних чисел).

З цього формулювання випливає, що обчислення x=log a b, рівнозначне рішенню рівняння a x = b.Наприклад, log 2 8 = 3тому що 8 = 2 3 . Формулювання логарифму дає можливість довести, що якщо b=a з, то логарифм числа bна підставі aдорівнює з. Також ясно, що тема логарифмування тісно пов'язана з темою ступеня числа.

З логарифмами, як і з будь-якими числами, можна виконувати операції складання, відніманняі всіляко трансформувати. Але через те, що логарифми — це не зовсім ординарні числа, тут застосовні свої особливі правила, які називаються основними властивостями.

Складання та віднімання логарифмів.

Візьмемо два логарифми з однаковими підставами: log a xі log a y. Тоді зними можна виконувати операції складання та віднімання:

Як бачимо, сума логарифмівдорівнює логарифму твору, а різниця логарифмів- Логарифму приватного. Причому це правильно якщо числа ахі упозитивні та а ≠ 1.

Важливо звертати увагу, що основним аспектом даних формулах виступають одні й самі підстави. Якщо підстави відрізняються одна від одної, ці правила не застосовуються!

Правила складання та віднімання логарифмів з однаковими підставами читаються не тільки зліва на право, а й на оборот. В результаті ми маємо теореми логарифму твору та логарифму приватного.

Логарифм творудвох позитивних чисел дорівнює сумі їх логарифмів ; перефразовуючи цю теоремуотримаємо наступне, якщо числа а, xі упозитивні та а ≠ 1, то:

Логарифм приватногодвох позитивних чисел дорівнює різниці логарифмів ділимого та дільника. Говорячи інакше, якщо числа а, хі упозитивні та а ≠ 1, то:

Застосуємо вищевикладені теореми на вирішення прикладів:

Якщо числа xі унегативні, то формула логарифму творустає безглуздою. Так, заборонено писати:

оскільки вирази log 2 (-8) і log 2 (-4) взагалі не визначені ( логарифмічна функція у= log 2 хвизначено лише для позитивних значеньаргументу х).

Теорема творузастосовна не тільки для двох, а й для необмеженого числаспівмножників. Це означає, що для будь-якого натурального kта будь-яких позитивних чисел x 1 , x 2 , . . . ,x nіснує тотожність:

З теореми логарифму приватногоможна отримати ще одну властивість логарифму. Загальновідомо, що log a 1= 0, отже,

А значить має місце рівність:

Логарифми двох взаємно зворотних чиселпо одному й тому підставі будуть різні друг від друга виключно знаком. Так:

Логарифм. Властивості логарифмів

Логарифм. Властивості логарифмів

Розглянемо рівність. Нехай нам відомі значення і ми хочемо знайти значення.

Тобто ми шукаємо показник ступеня, в який потрібно звести, щоб отримати .

Нехай змінна може приймати будь-яке дійсне значення, Тоді на змінні та накладаються такі обмеження: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

Якщо нам відомі значення і , і перед нами стоїть завдання знайти невідоме , то для цього вводиться математична дія, Яке називається логарифмування.

Щоб знайти значення, ми беремо логарифм числапо підставі :

Логарифмом числа на підставі називається показник ступеня, в який треба звести, щоб отримати .

Тобто основне логарифмічне тотожність:

o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

є по суті математичним записом визначення логарифму.

Математична операція логарифмування є зворотною по відношенню до операції зведення в ступінь, тому властивості логарифмівтісно пов'язані з властивостями ступеня.

Перерахуємо основні властивості логарифмів:

(o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

d>0″/>, 1″ title=”d1″/>

4.

5.

Наступна група властивостей дозволяє представити показник ступеня виразу, що стоїть під знаком логарифму, або стоїть на підставі логарифму як коефіцієнт перед знаком логарифму:

6.

7.

8.

9.

Наступна група формул дозволяє перейти від логарифму з цією основою до логарифму з довільною основою, і називається формулами переходу до нової основи:

10.

12. (наслідок з якості 11)

Наступні три властивості не дуже відомі, однак вони часто використовуються при вирішенні логарифмічних рівнянь або при спрощенні виразів, що містять логарифми:

13.

14.

15.

Приватні випадки:

— десятковий логарифм

— натуральний логарифм

При спрощенні виразів, що містять логарифми, застосовується загальний підхід:

1. Представляємо десяткові дробияк звичайних.

2. Змішані числаподаємо у вигляді неправильних дробів.

3. Числа, що стоять на підставі логарифму та під знаком логарифму розкладаємо на прості множники.

4. Намагаємось привести всі логарифми до однієї основи.

5. Застосовуємо властивості логарифмів.

Давайте розглянемо приклади спрощення виразів, що містять логарифми.

приклад 1.

Обчислити:

Спростимо всі показники ступенів: наше завдання привести їх до логарифмів, в основі яких стоїть те ж число, що й у підставі ступеня.

==(за якістю 7)=(за якістю 6) =

Підставимо показники, які у нас вийшли у вихідний вираз. Отримаємо:

Відповідь: 5,25

Приклад 2. Обчислити:

Приведемо всі логарифми до основи 6 (при цьому логарифми зі знаменника дробу «перекочують» до чисельника):

Розкладемо числа, що стоять під знаком логарифму на прості множники:

Застосуємо властивості 4 та 6:

Введемо заміну

Отримаємо:

Відповідь: 1

Логарифм . Основна логарифмічна тотожність.

Властивості логарифмів. Десятковий логарифм. Натуральний логарифм.

Логарифмом позитивного числа N на підставі (b > 0, b 1) називається показник ступеня x , в яку потрібно звести b щоб отримати N .

Цей запис рівнозначний наступному: b x = N .

Приміри: log 3 81 = 4 , так як 3 4 = 81 ;

log 1/3 27 = – 3, оскільки (1/3) - 3 = 3 3 = 27.

Наведене вище визначення логарифму можна записати у вигляді тотожності:

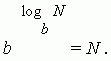
Основні властивості логарифмів.

2) log 1 = 0, так як b 0 = 1 .

3) Логарифм твору дорівнює сумі логарифмів співмножників:

4) Логарифм приватного дорівнює різниці логарифмів діленого та дільника:

5) Логарифм ступеня дорівнює добутку показника ступеня на логарифм її основи:

Наслідком цієї властивості є таке: логарифм кореня дорівнює логарифмупідкореного числа, поділеного на ступінь кореня:

6) Якщо на підставі логарифму знаходиться ступінь, то величину, зворотний показник ступеня, можна винести за знак лога риму:

Два останніх властивостіможна об'єднати в одне:

7) Формула модуля переходу (т. e. переходу від однієї основи логарифму до іншої основи):

В окремому випадку при N = aмаємо:

Десятичним логарифмом називається логарифм з основи 10. Він позначається lg, тобто. log 10 N= lg N. Логарифми чисел 10, 100, 1000, . p авни відповідно 1, 2, 3, …, тобто. мають стільки позитивних

одиниць, скільки нулів стоїть у логарифмованій кількості після одиниці. Логарифми чисел 0.1, 0.01, 0.001, . p авни відповідно –1, –2, –3, …, тобто. мають стільки негативних одиниць, скільки нулів стоїть в логарифмується перед одиницею (вважаючи і нуль цілих). Логарифми інших чисел мають дробову частинузвану мантисою. Ціла частиналогарифма називається характеристикою. Для практичного застосування десяткові логарифми найбільш зручні.

Натуральним логарифмом називається логарифм з основи е. Він позначається ln, тобто. log e N= ln N. Число еє ірраціональним, його наближене значення 2.718281828. Воно є межею, якої прагне число (1 + 1 / n) nпри необмеженому зростанні n(Див. перший чудова межа на сторінці «Межі числових послідовностей»).
Як це не здасться дивним, натуральні логарифмивиявилися дуже зручними під час проведення різного родуоперацій, пов'язаних із аналізом функцій. Обчислення логарифмів на підставі ездійснюється набагато швидше, ніж з будь-якої іншої основи.

Що потрібно сьогодні для усиновлення дитини у Росії? Усиновлення у Росії, крім відповідального особистого рішення, передбачає низку процедур державної перевірки кандидатів. Жорсткий відбір на підготовчому етапісприяє більше […]
Відомості безкоштовно по ІПН або ОГРН з реєстру податкової по всій Росії - онлайн На Єдиному порталіПодаткові послуги можуть бути отримані відомостями про державної реєстрації юридичних осіб, індивідуальних підприємців, […]
Покарання за їзду без документів ( водійські права, страховка, СТС) Іноді по забудькуватості водії сідають за кермо без ВУ та отримують штраф за їзду без документів. Нагадаємо, що автоаматор за кермом при собі в обов'язковому порядку […]
Квіти чоловіків. Які квіти можна подарувати чоловікові? Які квіти можна подарувати чоловікові? "Чоловічих" квітів не так багато, але є такі, які дарують чоловікам. Маленький список квітів перед вами: Хризантеми. Троянди. Гвоздики. […]
Службова записка– це спеціальна формадокумента, що використовується в внутрішньому середовищіпідприємства та служить для швидкого вирішенняпоточні виробничі проблеми. Зазвичай цей документ складається з метою внесення будь-якого […]
Коли і як отримати накопичувальну частину пенсії в Ощадбанку? Ощадбанк є банк-партнер державного пенсійного фонду. На підставі цього громадяни, які оформили накопичувальну пенсію, могли переводити до нього накопичувальну частину […]
Дитячі посібники в Ульяновську та Ульянівської областіу 2018 році Крім того, у всіх суб'єктах працюють програми, затверджені федеральним законодавством. Розберемо, хто та на які пільги може розраховувати. Як регіональна влада […]
Детальний посібник, як скласти довіреність на представлення інтересів фізичної особиу суді У цивільному чи арбітражному позові, в адміністративній чи кримінальній справі інтереси і позивача, і відповідача можуть представлятися повіреним: […]

основними властивостями.

logax + logay = loga (x · y);
logax – logay = loga (x: y).

однакові підстави

Log6 4+log6 9.

Тепер трохи ускладнимо завдання.

Приклади вирішення логарифмів

Що, якщо у підставі чи аргументі логарифма стоїть ступінь? Тоді показник цього ступеня можна винести за знак логарифму за такими правилами:

Зрозуміло, всі ці правила мають сенс за дотримання ОДЗ логарифму: a > 0, a ≠ 1, x >

Завдання. Знайдіть значення виразу:

Перехід до нової основи

Нехай даний логарифм logax. Тоді для будь-якого числа c такого, що c > 0 і c ≠ 1, правильна рівність:

Завдання. Знайдіть значення виразу:

Дивіться також:

Основні властивості логарифму

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Експонента дорівнює 2,718281828. Щоб запам'ятати експоненту, можете вивчити правило: експонента дорівнює 2,7 і двічі рік народження Льва Миколайовича Толстого.

Основні властивості логарифмів

Знаючи це правило знатимете і точне значенняекспоненти та дату народження Льва Толстого.

Приклади на логарифми

Прологарифмувати вирази

приклад 1.
а). х=10ас^2 (а>0,с>0).

За властивостями 3,5 обчислюємо

4. де .

Приклад 2. Знайти х, якщо

Приклад 3. Нехай задано значення логарифмів

Обчислити log(x), якщо

Основні властивості логарифмів

Логарифми, як і будь-які числа, можна складати, віднімати та всіляко перетворювати. Але оскільки логарифми — це не зовсім звичайні числа, тут є свої правила, які називаються основними властивостями.

Ці правила обов'язково треба знати - без них не вирішується жодне серйозне логарифмічне завдання. До того ж їх зовсім небагато — все можна вивчити за один день. Отже, почнемо.

Додавання та віднімання логарифмів

Розглянемо два логарифми з однаковими підставами: logax та logay. Тоді їх можна складати і віднімати, причому:

logax + logay = loga (x · y);
logax – logay = loga (x: y).

Отже, сума логарифмів дорівнює логарифму твору, а різниця - приватного логарифму. Зверніть увагу: ключовий момент тут однакові підстави. Якщо підстави різні, ці правила не працюють!

Ці формули допоможуть обчислити логарифмічний вираз навіть тоді, коли окремі його частини не рахуються (див. урок «Що таке логарифм»). Погляньте на приклади і переконайтеся:

Оскільки підстави у логарифмів однакові, використовуємо формулу суми:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.

Завдання. Знайдіть значення виразу: log2 48 − log2 3.

Підстави однакові, використовуємо формулу різниці:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Завдання. Знайдіть значення виразу: log3 135 − log3 5.

Знову підстави однакові, тому маємо:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Як бачите, вихідні вирази складені з поганих логарифмів, які окремо не вважаються. Але після перетворень виходять цілком нормальні числа. На цьому факті збудовано багато контрольних робіт. Так що контрольні — подібні висловлювання на повному серйозі (іноді практично без змін) пропонуються на ЄДІ.

Винесення показника ступеня з логарифму

Неважко помітити, що останнє правило слідує їх перших двох. Але краще його все ж таки пам'ятати — у деяких випадках це значно скоротить обсяг обчислень.

Зрозуміло, всі ці правила мають сенс за дотримання ОДЗ логарифму: a > 0, a ≠ 1, x > 0. І ще: вчитеся застосовувати всі формули як зліва направо, а й навпаки, тобто. можна вносити числа, що стоять перед знаком логарифму, до самого логарифму. Саме це найчастіше й потрібне.

Завдання. Знайдіть значення виразу: log7 496.

Позбавимося ступеня в аргументі за першою формулою:
log7 496 = 6 · log7 49 = 6 · 2 = 12

Завдання. Знайдіть значення виразу:

Зауважимо, що у знаменнику стоїть логарифм, основа та аргумент якого є точними ступенями: 16 = 24; 49 = 72. Маємо:

Думаю, до останнього прикладу потрібні пояснення. Куди зникли логарифми? До останнього моменту ми працюємо лише зі знаменником.

Формули логарифмів. Логарифми – приклади рішення.

Представили підставу і аргумент логарифму, що там стоїть, у вигляді ступенів і винесли показники — отримали «триповерховий» дріб.

Тепер подивимося на основний дріб. У чисельнику і знаменнику стоїть те саме число: log2 7. Оскільки log2 7 ≠ 0, можемо скоротити дріб — у знаменнику залишиться 2/4. За правилами арифметики, четвірку можна перенести в чисельник, що було зроблено. В результаті вийшла відповідь: 2.

Перехід до нової основи

На допомогу приходять формули переходу до нової основи. Сформулюємо їх як теореми:

Нехай даний логарифм logax. Тоді для будь-якого числа c такого, що c > 0 і c ≠ 1, правильна рівність:

Зокрема, якщо покласти c = x отримаємо:

Ці формули рідко зустрічається у звичайних числових виразах. Оцінити, наскільки вони зручні, можна лише при розв'язанні логарифмічних рівнянь та нерівностей.

Завдання. Знайдіть значення виразу: log5 16 · log2 25.

Зауважимо, що в аргументах обох логарифмів стоять точні ступені. Винесемо показники: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

А тепер «перевернемо» другий логарифм:

Завдання. Знайдіть значення виразу: log9 100 · lg 3.

Підстава та аргумент першого логарифму — точні ступені. Запишемо це і позбудемося показників:

Тепер позбудемося десяткового логарифму, перейшовши до нової основи:

Основне логарифмічне тотожність

У першому випадку число n стає показником ступеня, що стоїть у аргументі. Число n може бути абсолютно будь-яким, адже це просто значення логарифму.

Друга формула – це фактично перефразоване визначення. Вона і називається: .

Справді, що буде, якщо число b звести на такий ступінь, що число b у цій мірі дає число a? Правильно: вийде це саме число a. Уважно прочитайте цей абзац ще раз — багато хто на ньому «зависає».

Подібно до формул переходу до нової основи, основна логарифмічна тотожність іноді буває єдино можливим рішенням.

Завдання. Знайдіть значення виразу:

Зауважимо, що log25 64 = log5 8 — просто винесли квадрат із підстави та аргументу логарифму. Враховуючи правила множення ступенів з однаковою основою, отримуємо:

Якщо хтось не в курсі, це було справжнє завдання з ЄДІ 🙂

Логарифмічна одиниця та логарифмічний нуль

Насамкінець наведу дві тотожності, які складно назвати властивостями — швидше, це наслідки з визначення логарифму. Вони постійно зустрічаються у завданнях і, що дивно, створюють проблеми навіть для «просунутих» учнів.

logaa = 1 – це. Запам'ятайте раз і назавжди: логарифм з будь-якої основи a від самої цієї основи дорівнює одиниці.
loga 1 = 0 це. Підстава a може бути будь-якою, але якщо в аргументі стоїть одиниця — логарифм дорівнює нулю! Тому що a0 = 1 — це прямий наслідок визначення.

Ось і всі властивості. Обов'язково потренуйтеся застосовувати їх на практиці! Завантажте шпаргалку на початку уроку, роздрукуйте її і вирішуйте завдання.

Дивіться також:

Логарифмом числа b на підставі a позначають вираз . Обчислити логарифм означає знайти такий ступінь x (), при якому виконується рівність

Основні властивості логарифму

Наведені властивості необхідно знати, оскільки, на їх основі вирішуються практично всі завдання та приклади пов'язані з логарифмами. Інші екзотичні властивості можна вивести шляхом математичних маніпуляцій з даними формулами

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

При обчисленнях формули суми та різниці логарифмів (3,4) зустрічаються досить часто. Інші дещо складні, але у ряді завдань є незамінними для спрощення складних виразів та обчислення їх значень.

Поширені випадки логарифмів

Одними з поширених логарифмів є такі в яких основа рівна десять, експоненті або двійці.
Логарифм на основі десять прийнято називати десятковим логарифмом і спрощено позначати lg(x).

Із запису видно, що основи запису не пишуть. Для прикладу

Натуральний логарифм – це логарифм, у якого за основу експонента (позначають ln(x)).

Експонента дорівнює 2,718281828. Щоб запам'ятати експоненту, можете вивчити правило: експонента дорівнює 2,7 і двічі рік народження Льва Миколайовича Толстого. Знаючи це правило знатимете і точне значення експоненти, і дату народження Льва Толстого.

І ще один важливий логарифм на основі два позначають

Похідна від логарифм функції дорівнює одиниці розділеної на змінну

Інтеграл чи первісна логарифма визначається залежністю

Наведеного матеріалу Вам достатньо, щоб вирішувати широкий клас завдань, пов'язаних з логарифмами та логарифмування. Для засвоєння матеріалу наведу лише кілька поширених прикладів з шкільної програмита ВНЗ.

Приклади на логарифми

Прологарифмувати вирази

приклад 1.
а). х=10ас^2 (а>0,с>0).

За властивостями 3,5 обчислюємо

2.
За властивістю різниці логарифмів маємо

3.
Використовуючи властивості 3,5 знаходимо

4. де .

На вигляд складний виразз використанням ряду правил спрощується до вигляду

Знаходження значень логарифмів

Приклад 2. Знайти х, якщо

Рішення. Для обчислення застосуємо до останнього доданку 5 і 13 властивості

Підставляємо в запис і сумуємо

Оскільки основи рівні, то прирівнюємо вирази

Логарифми. Початковий рівень.

Нехай задано значення логарифмів

Обчислити log(x), якщо

Рішення: Прологарифмуємо змінну, щоб розписати логарифм через суму доданків

На цьому знайомство з логарифмами та їх властивостями лише починається. Вправляйтеся в обчисленнях, збагачуйте практичні навички - отримані знання скоро знадобляться для вирішення логарифмічних рівнянь. Вивчивши основні методи розв'язання таких рівнянь, ми розширимо Ваші знання для іншої. важливій темі- Логарифмічні нерівності ...

Основні властивості логарифмів

Додавання та віднімання логарифмів

Розглянемо два логарифми з однаковими підставами: logax та logay. Тоді їх можна складати і віднімати, причому:

logax + logay = loga (x · y);
logax – logay = loga (x: y).

Завдання. Знайдіть значення виразу: log6 4 + log6 9.

Оскільки підстави у логарифмів однакові, використовуємо формулу суми:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.

Завдання. Знайдіть значення виразу: log2 48 − log2 3.

Підстави однакові, використовуємо формулу різниці:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Завдання. Знайдіть значення виразу: log3 135 − log3 5.

Знову підстави однакові, тому маємо:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Винесення показника ступеня з логарифму

Як вирішувати логарифми

Саме це найчастіше й потрібне.

Завдання. Знайдіть значення виразу: log7 496.

Позбавимося ступеня в аргументі за першою формулою:
log7 496 = 6 · log7 49 = 6 · 2 = 12

Завдання. Знайдіть значення виразу:

Зауважимо, що у знаменнику стоїть логарифм, основа та аргумент якого є точними ступенями: 16 = 24; 49 = 72. Маємо:

Думаю, до останнього прикладу потрібні пояснення. Куди зникли логарифми? До останнього моменту ми працюємо лише зі знаменником. Представили підставу і аргумент логарифму, що там стоїть, у вигляді ступенів і винесли показники — отримали «триповерховий» дріб.

Перехід до нової основи

На допомогу приходять формули переходу до нової основи. Сформулюємо їх як теореми:

Нехай даний логарифм logax. Тоді для будь-якого числа c такого, що c > 0 і c ≠ 1, правильна рівність:

Зокрема, якщо покласти c = x отримаємо:

Завдання. Знайдіть значення виразу: log5 16 · log2 25.

Зауважимо, що в аргументах обох логарифмів стоять точні ступені. Винесемо показники: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

А тепер «перевернемо» другий логарифм:

Завдання. Знайдіть значення виразу: log9 100 · lg 3.

Підстава та аргумент першого логарифму — точні ступені. Запишемо це і позбудемося показників:

Тепер позбудемося десяткового логарифму, перейшовши до нової основи:

Основне логарифмічне тотожність

Друга формула – це фактично перефразоване визначення. Вона і називається: .

Завдання. Знайдіть значення виразу:

Якщо хтось не в курсі, це було справжнє завдання з ЄДІ 🙂

Логарифмічна одиниця та логарифмічний нуль

logaa = 1 – це. Запам'ятайте раз і назавжди: логарифм з будь-якої основи a від самої цієї основи дорівнює одиниці.
loga 1 = 0 це. Підстава a може бути будь-якою, але якщо в аргументі стоїть одиниця — логарифм дорівнює нулю! Тому що a0 = 1 — це прямий наслідок визначення.

Зворотна функція логарифму. Формули логарифмів

Складання та віднімання логарифмів.

Розділ 2. Елементи вищої математики.

2.1. Механічний сенс похідної.

Збір та використання персональної інформації

Розкриття інформації третім особам

Захист персональної інформації

Дотримання вашої конфіденційності на рівні компанії

Логарифми. Властивості логарифмів

Завдання та тести на тему «Логорифми. Властивості логарифмів»

Властивості логарифмів, формулювання та докази.

Основні властивості логарифмів, формули

Формулювання та докази властивостей

Основні властивості логарифмів

Додавання та віднімання логарифмів

Винесення показника ступеня з логарифму

Перехід до нової основи

Основне логарифмічне тотожність

Логарифмічна одиниця та логарифмічний нуль

Логарифм. Властивості логарифму (складання та віднімання).

Складання та віднімання логарифмів.

Логарифм. Властивості логарифмів

Приклади вирішення логарифмів

Перехід до нової основи

Основні властивості логарифму

Основні властивості логарифмів

Приклади на логарифми

Прологарифмувати вирази

Основні властивості логарифмів

Додавання та віднімання логарифмів

Винесення показника ступеня з логарифму

Формули логарифмів. Логарифми – приклади рішення.

Перехід до нової основи

Основне логарифмічне тотожність

Логарифмічна одиниця та логарифмічний нуль

Основні властивості логарифму

Поширені випадки логарифмів

Приклади на логарифми

Прологарифмувати вирази

Знаходження значень логарифмів

Логарифми. Початковий рівень.

Основні властивості логарифмів

Додавання та віднімання логарифмів

Винесення показника ступеня з логарифму

Як вирішувати логарифми

Перехід до нової основи

Основне логарифмічне тотожність

Логарифмічна одиниця та логарифмічний нуль