Послідовність визначення та основні характеристики. Поняття числової послідовності
Логарифмом позитивного числа b на підставі a (a>0, a не дорівнює 1) називають таке число з, що a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0) nbsp
Зверніть увагу: логарифм від позитивного числа не визначено. Крім того, в основі логарифму має бути позитивне число, не рівне 1. Наприклад, якщо ми зведемо -2 у квадрат, отримаємо число 4, але це не означає, що логарифм на підставі -2 від 4 дорівнює 2.
Основне логарифмічне тотожність
a log a b = b (a > 0, a ≠ 1) (2)Важливо, що області визначення правої та лівої частин цієї формули відрізняються. Ліва частинавизначено лише за b>0, a>0 і a ≠ 1. Права частина визначена за будь-якого b, а від a взагалі не залежить. Таким чином, застосування основної логарифмічної "тотожності" при вирішенні рівнянь та нерівностей може призвести до зміни ОДЗ.
Два очевидні наслідки визначення логарифму
log a a = 1 (a > 0, a ≠ 1) (3)log a 1 = 0 (a > 0, a ≠ 1) (4)
Дійсно, при зведенні числа a в першу міру ми отримаємо те саме число, а при зведенні в нульовий ступінь - одиницю.
Логарифм твору та логарифм приватного
log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)
Хотілося б застерегти школярів від бездумного застосування цих формул під час вирішення логарифмічних рівняньта нерівностей. При їх використанні "зліва направо" відбувається звуження ОДЗ, а при переході від суми чи різниці логарифмів до логарифму твору або приватного - розширення ОДЗ.
Дійсно, вираз log a (f (x) g (x)) визначено у двох випадках: коли обидві функції суворо позитивні або коли f (x) і g (x) обидві менше від нуля.
Перетворюючи цей вираз у суму log a f (x) + log a g (x) , ми змушені обмежуватися лише випадком, коли f(x)>0 і g(x)>0. В наявності звуження області допустимих значень, а це категорично неприпустимо, тому що може призвести до втрати рішень. Аналогічна проблема існує й у формули (6).
Ступінь можна виносити за знак логарифму
log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)І знову хотілося б покликати до акуратності. Розглянемо наступний приклад:
Log a (f(x) 2 = 2 log a f(x)
Ліва частина рівності визначена, очевидно, за всіх значень f(х), крім нуля. Права частина - тільки за f(x)>0! Виносячи ступінь із логарифму, ми знову звужуємо ОДЗ. Зворотна процедура призводить до розширення області допустимих значень. Всі ці зауваження стосуються не тільки ступеня 2, але й будь-якого парного ступеня.
Формула переходу до нової основи
log a b = log c b log ca (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)Той рідкісний випадок, коли ОДЗ не змінюється під час перетворення. Якщо ви розумно вибрали основу з (позитивна і не рівна 1), формула переходу до нової основи є абсолютно безпечною.
Якщо в якості нової основи вибрати число b, отримаємо важливий окремий випадокформули (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Декілька простих прикладів з логарифмами
Приклад 1. Обчисліть: lg2 + lg50.
Рішення. lg2 + lg50 = lg100 = 2. Ми скористалися формулою суми логарифмів (5) та визначенням десяткового логарифму.
Приклад 2. Розрахуйте: lg125/lg5.
Рішення. lg125/lg5 = log 5 125 = 3. Ми використали формулу переходу до нової основи (8).
Таблиця формул, пов'язаних із логарифмами
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log ca (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
Одним із елементів алгебри примітивного рівня є логарифм. Назва походить з грецької мовивід слова "число" або "ступінь" і означає ступінь, в який необхідно звести число, що знаходиться в підставі, для знаходження підсумкового числа.
Види логарифмів
- log a b – логарифм числа b на підставі a (a > 0, a ≠ 1, b > 0);
- lg b – десятковий логарифм (логарифм на підставі 10, a = 10);
- ln b - натуральний логарифм (логарифм на основі e, a = e).
Як вирішувати логарифми?
Логари́м числа b за основою a є показником ступеня, який вимагає, щоб у число b звели основу а. Отриманий результат вимовляється так: "логарифм b на підставі а". Розв'язання логарифмічних завдань полягає в тому, що вам необхідно визначити цей ступінь за числами вказаним числам. Існують деякі основні правила, щоб визначити чи вирішити логарифм, а також перетворити сам запис. Використовуючи їх, здійснюється рішення логарифмічних рівнянь, знаходяться похідні, вирішуються інтеграли та здійснюються багато інших операцій. В основному, рішенням самого логарифму є його спрощений запис. Нижче наведено основні формули та властивості:
Для будь-яких a; a > 0; a ≠ 1 і для будь-яких x; y > 0.
- a log a b = b – основна логарифмічна тотожність
- log a 1 = 0
- log a a = 1
- log a (x · y) = log a x + log a y
- log a x / y = log a x - log a y
- log a 1/x = -log a x
- log a x p = p log a x
- log a k x = 1/k · log a x , при k ≠ 0
- log a x = log a c x c
- log a x = log b x / log b a – формула переходу до нової основи
- log a x = 1/log x a


Як вирішувати логарифми – покрокова інструкція рішення
- Спочатку запишіть необхідне рівняння.
Зверніть увагу: якщо в логарифмі з основи стоїть 10 , запис укорочується, виходить десятковий логарифм. Якщо стоїть натуральне числотобто записуємо, скорочуючи до натурального логарифму. Мається на увазі, що результат всіх логарифмів - ступінь, в який зводиться число підстав до отримання числа b.


Безпосередньо рішення і полягає у обчисленні цього ступеня. Перш ніж вирішити вираз із логарифмом, його необхідно спростити за правилом, тобто, користуючись формулами. Основні тотожності ви зможете знайти, повернувшись трохи назад у статті.
Складаючи та віднімаючи логарифми з двома різними числами, але з однаковими підставами, замінюйте одним логарифмом з добутком чи розподілом чисел b та з відповідно. У такому разі можна застосувати формулу переходу до іншої основи (див. вище).
Якщо ви використовуєте вирази для спрощення логарифму, необхідно враховувати деякі обмеження. Тобто: основа логарифму а – лише позитивне число, але з рівне одиниці. Число b, як і а, має бути більше нуля.
Є випадки, коли спростивши вираз, ви не зможете обчислити логарифм у числовому вигляді. Буває, що такий вираз не має сенсу, адже багато ступенів – ірраціональні числа. За такої умови залиште рівень числа у вигляді запису логарифму.




-
Перевірте, чи не стоять під знаком логарифму негативні числачи одиниця. Цей методзастосуємо до виразів виду log b (x) log b (a) (\displaystyle (\frac (\log _(b)(x))(\log _(b)(a)))). Однак він не підходить для деяких особливих випадків:
- Логарифм негативного числа не визначено за будь-якої підстави (наприклад, log (− 3) (\displaystyle \log(-3))або log 4 (− 5) (\displaystyle \log _(4)(-5))). У цьому випадку напишіть "ні рішення".
- Логарифм нуля з будь-якої основи також не визначено. Якщо вам попався ln (0) (\displaystyle \ln(0)), запишіть "ні рішення".
- Логарифм одиниці з будь-якої основи ( log (1) (\displaystyle \log(1))) завжди дорівнює нулю, оскільки x 0 = 1 (\displaystyle x^(0)=1)для всіх значень x. Запишіть замість такого логарифму 1 і не використовуйте наведений нижче метод.
- Якщо логарифми мають різні підстави, наприклад l o g 3 (x) l o g 4 (a) (\displaystyle (\frac (log_(3)(x))(log_(4)(a)))), і зводяться до цілим числам, значення висловлювання не можна знайти вручну.
-
Перетворіть вираз на один логарифм.Якщо вираз не відноситься до наведених вище особливим випадкам, його можна подати у вигляді одного логарифму. Використовуйте для цього таку формулу: log b (x) log b (a) = log a (x) (\displaystyle (\frac (\log _(b)(x))(\log _(b)(a)))=\ log _(a)(x)).
- Приклад 1: розглянемо вираз log 16 log 2 (\displaystyle (\frac (\log (16))(\log (2)))).
Для початку подаємо вираз у вигляді одного логарифму за допомогою наведеної вище формули: log 16 log 2 = log 2 (16) (\displaystyle (\frac (\log (16))(\log (2)))=\log _(2)(16)). - Ця формула " заміни основи " логарифму виводиться з основних властивостей логарифмів.
- Приклад 1: розглянемо вираз log 16 log 2 (\displaystyle (\frac (\log (16))(\log (2)))).
-
При можливості обчисліть значення виразу вручну.Щоб знайти log a (x) (\displaystyle \log _(a)(x)), уявіть собі вираз " a? = x (\displaystyle a^(?)=x)", тобто поставте наступне питання: "У яку міру необхідно звести a, Щоб отримати x?". Для відповіді на це запитання може знадобитися калькулятор, але якщо вам пощастить, ви зможете знайти його вручну.
- Приклад 1 (продовження): Перепишіть у вигляді 2? = 16 (\displaystyle 2^(?)=16). Необхідно знайти, скільки має стояти замість знака "?". Це можна зробити методом спроб і помилок:
2 2 = 2 ∗ 2 = 4 (\displaystyle 2^(2)=2*2=4)
2 3 = 4 ∗ 2 = 8 (\displaystyle 2^(3)=4*2=8)
2 4 = 8 ∗ 2 = 16 (\displaystyle 2^(4)=8*2=16)
Отже, шуканим числом є 4: log 2 (16) (\displaystyle \log _(2)(16)) = 4 .
- Приклад 1 (продовження): Перепишіть у вигляді 2? = 16 (\displaystyle 2^(?)=16). Необхідно знайти, скільки має стояти замість знака "?". Це можна зробити методом спроб і помилок:
-
Залишіть відповідь у логарифмічній формі, якщо вам не вдається спростити її.Багато логарифмів дуже складно обчислити вручну. У цьому випадку, щоб отримати точну відповідь, вам знадобиться калькулятор. Однак якщо ви вирішуєте завдання на уроці, то вчителі, швидше за все, задовольнять відповідь у логарифмічному вигляді. Нижче розглянутий метод використаний на вирішення складнішого прикладу:
- приклад 2: чому одно log 3 (58) log 3 (7) (\displaystyle (\frac (\log _(3)(58))(\log _(3)(7))))?
- Перетворимо цей вислів на один логарифм: log 3 (58) log 3 (7) = log 7 (58) (\displaystyle (\frac (\log _(3)(58))(\log _(3)(7)))=\ log _(7)(58)). Зверніть увагу, що загальна для обох логарифмів основа 3 зникає; це справедливо для будь-якої основи.
- Перепишемо вираз у вигляді 7? = 58 (\displaystyle 7^(?)=58)і спробуємо знайти значення?
7 2 = 7 ∗ 7 = 49 (\displaystyle 7^(2)=7*7=49)
7 3 = 49 ∗ 7 = 343 (\displaystyle 7^(3)=49*7=343)
Оскільки 58 між цими двома числами, не виражається цілим числом. - Залишаємо відповідь у логарифмічному вигляді: log 7 (58) (\displaystyle \log _(7)(58)).
274. Зауваження.
а)Якщо у виразі, який потрібно обчислити, зустрічається сумаабо різницячисел, їх треба знаходити без допомоги таблиць звичайним додаваннямчи відніманням. Напр.
log (35 +7,24) 5 = 5 log (35 + 7,24) = 5 log 42,24.
б)Вміючи логарифмувати вирази, ми можемо, назад, по даному результатулогарифмування знайти той вираз, від якого вийшов цей результат; так, якщо
log х= log a+ log b- 3 log з,
то легко збагнути, що
в)Перш ніж перейти до розгляду устрою логарифмічних таблиць, ми вкажемо деякі властивості десяткових логарифмів, тобто. таких, у яких за основу прийнято число 10 (тільки такі логарифми використовуються для обчислень).
Розділ другий.
Властивості десяткових логарифмів.
275 . а) Так як 10 1 = 10, 10 2 = 100, 10 3 = 1000, 10 4 = 10000 і т. д., то log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4, т.д.
Значить, логарифм цілого числа, що зображується одиницею з нулями, є ціле позитивне число, що містить стільки одиниць, скільки нулів у зображенні числа.
Таким чином: log 100000 = 5, log 1000 000 = 6 , і т.д.
б) Так як

log 0,1 = -l; log 0,01 = - 2; log 0,001 == -3; log 0,0001 = - 4,і т.д.
Значить, логарифм десяткового дробу, що зображується одиницею з попередніми нулями, є ціле негативне число містить стільки негативних одиниць, скільки нулів у зображенні дробу, вважаючи навіть 0 цілих.
Таким чином: log 0,00001 = - 5, log 0,000001 = -6,і т.д.
в)Візьмемо ціле число, яке не зображується одиницею з нулями, напр. 35 або ціле число з дробом, напр. 10,7. Логарифм такого числа не може бути цілим числом, оскільки, піднявши 10 ступінь з цілим показником (позитивним або негативним), ми отримаємо 1 з нулями (наступними за 1, або їй попередніми). Припустимо тепер, що логарифм такого числа є якийсь дріб a / b . Тоді ми мали б рівність

Але ці рівності неможливі, як 10а є 1 з нулями, тоді як ступеня 35b і 10,7b ні за якого показника b не можуть дати 1 з нулями. Отже, не можна допустити, щоб log 35і log 10,7дорівнювали дробам. Але з властивостей логарифмічної функції ми знаємо (), що будь-яке позитивне число має логарифм; отже, кожне з чисел 35 і 10,7 має свій логарифм, і оскільки він не може бути ні числом цілим, ні числом дробовим, тобто число ірраціональне і, отже, не може бути виражений точно за допомогою цифр. Зазвичай ірраціональні логарифми виражають приблизно у вигляді десяткового дробу з кількома десятковими знаками. Ціла кількість цього дробу (хоча б це було „0 цілих") називається характеристикоюа дробова частина - мантисою логарифму. Якщо, наприклад, логарифм є 1,5441 , то характеристика його дорівнює 1 , а мантіса є 0,5441 .
г)Візьмемо якесь ціле чи змішане число, напр. 623 або 623,57 . Логарифм такого числа складається з характеристики та мантиси. Виявляється, що десяткові логарифмимають ту зручність, що характеристику їх ми завжди можемо знайти за одним видом числа . Для цього порахуємо, скільки цифр у даному цілому числі, або в цілій частині змішаного числа, У прикладах цих цифр 3 . Тому кожне з чисел 623 і 623,57 більше 100 але менше 1000; значить, і логарифм кожного з них більший log 100, тобто більше 2 , але менше log 1000, тобто менше 3 (Згадаймо, що більше має і більший логарифм). Отже, log 623 = 2,..., і log 623,57 = 2,... (крапки замінюють собою невідомі мантиси).
Подібно до цього знайдемо:
|
10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,... |
1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,... |
Нехай взагалі в цій цілій кількості, або в цілій частині даного змішаного числа, міститься m цифр. Оскільки щонайменше ціле число, що містить m цифр, є 1 з m - 1 нулями на кінці, то (позначаючи це число N) можемо написати нерівності:
![]()
і, отже,
m - 1 < log N < m ,
log N = ( m - 1) + позитивний дріб .
Отже, характеристика logN = m - 1 .
Ми бачимо таким чином, що характеристика логарифму цілого чи змішаного числа містить стільки позитивних одиниць, скільки цифр у цілій частині числа без однієї.
Помітивши це, ми можемо прямо писати:
log 7,205 = 0, ...; log 83 = 1, ...; log 720,4 = 2,...і т.п.
д)Візьмемо кілька десяткових дробів, менших 1 (т. е. мають 0 цілих): 0,35; 0,07; 0,0056; 0,0008, і т.п.
Таким чином, кожен із цих логарифмів укладений між двома цілими негативними числами, що розрізняються на одну одиницю; тому кожен із них дорівнює меншому з цих негативних чисел, збільшеному на деякий позитивний дріб. напр. log0,0056 = -3 + позитивний дріб. Припустимо, що цей дріб буде 0,7482. Тоді, значить:
log 0,0056 = - 3 + 0,7482 (= - 2,2518).
Такі суми, як - 3 + 0,7482 , що складаються з цілого негативного числа.і позитивного десяткового дробу, умовилися при логарифмічних обчисленнях писати скорочено так: 3 ,7482 (Таке число читається: 3 з мінусом, 7482 десятитисячні.), тобто ставлять знак мінус над характеристикою з метою показати, що він відноситься тільки до цієї характеристики, а не до мантиси, яка залишається позитивною. Таким чином, із наведеної вище таблички видно, що
log 0,35 == 1, ....; log 0,07 = 2, ....; log 0,0008 = 4,.
Нехай взагалі ![]() . є десятковий дріб, у якого перед першим значущою цифрою α
стоїть m
нулів, рахуючи навіть 0 цілих. Тоді, очевидно, що
. є десятковий дріб, у якого перед першим значущою цифрою α
стоїть m
нулів, рахуючи навіть 0 цілих. Тоді, очевидно, що

- m < log A < - (m- 1).
Бо з двох цілих чисел: - m і - (m- 1) менше є - m , то
log А = - m+ позитивний дріб,
і тому характеристика log А = - m (При позитивній мантисі).
Таким чином, характеристика логарифму десяткового дробу, меншого 1, містить у собі стільки негативних одиниць, скільки нулів у зображенні десяткового дробу перед першою значущою цифрою, вважаючи навіть нуль цілих; мантиса ж такого логарифму позитивна.
е)Помножимо якесь число N(ціле або дробове - все одно) на 10, на 100 на 1000 ..., взагалі на 1 з нулями. Подивимося, як від цього зміниться log N. Тому що логарифм твору дорівнює сумілогарифмів співмножників, то
log (N 10) = log N + log 10 = log N + 1;
log (N 100) = log N + log 100 = log N + 2;
log (N 1000) = log N + log 1000 = log N + 3;і т.д.
Коли до log Nми додаємо якесь ціле число, то це число ми може завжди додавати до характеристики, а не до мантиси.
Тож якщо log N = 2,7804, то 2,7804 + 1 =3,7804; 2,7804 + 2 = 4,7801 тощо;
або якщо log N = 3,5649, то 3,5649 + 1 = 2,5649; 3,5649 + 2 = 1,5649, тощо.
Від множення числа на 10, 100, 1000,.., взагалі на 1 з нулями, мантиса логарифма не змінюється, а характеристика збільшується на стільки одиниць, скільки нулів у множнику .
Подібно до цього, взявши до уваги, що логарифм приватного дорівнює логарифмуділимого без логарифму дільника, ми отримаємо:
log N/10 = log N-log 10 = log N -1;
log N/100 = log N-log 100 = log N -2;
log N/1000 = log N-log 1000 = log N -3;і т.п.
Якщо умовимося при відніманні цілого числа з логарифму віднімати це ціле число завжди з характеристики, а мантису залишати без зміни, то можна сказати:
Від розподілу числа на 1 з нулями мантиса логарифма не змінюється, а характеристика зменшується на стільки одиниць, скільки нулів у дільнику.
276. Наслідки.З якості ( е) можна вивести такі два наслідки:
а) Мантіса логарифму десяткового числа не змінюється від перенесення в числі коми , Тому що перенесення коми рівносильне множенню або поділу на 10, 100, 1000 і т. д. Таким чином, логарифми чисел:
0,00423, 0,0423, 4,23, 423
відрізняються лише характеристиками, але з мантисами (за умови, що це мантиси позитивні).
б) Мантиси чисел, що мають одну і ту ж значну частину, але що відрізняються лише нулями на кінці, однакові: так, логарифми чисел: 23, 230, 2300, 23 000 відрізняються лише характеристиками.
Зауваження. З зазначених властивостейдесяткових логарифмів видно, що характеристику логарифму цілого числа та десяткового дробу ми можемо знаходити без допомоги таблиць (у цьому полягає велика зручністьдесяткових логарифмів); внаслідок цього в логарифмічних таблицях містяться лише одні мантиси; крім того, оскільки знаходження логарифмів дробів зводиться до знаходження логарифмів цілих чисел (логарифм дробу = логарифму чисельника без логарифму знаменника), то таблицях містяться мантиси логарифмів тільки цілих чисел.
Розділ третій.
Влаштування та вживання чотиризначних таблиць.
277. Системи логарифмів.Системою логарифмів називається сукупність логарифмів, обчислених для низки послідовних цілих чисел з однієї й тому підставі. Вживаються дві системи: система звичайних чи десяткових логарифмів, у яких за основу взято число 10 , і система так званих натуральних логарифмів, у яких за основу (з деяких причин, які усвідомлюються в інших відділах математики) взято ірраціональне число 2,7182818 ... Для обчислень використовуються десяткові логарифми, внаслідок тих зручностей, які ми вказані, коли ми перераховували властивості таких логарифмів.
Натуральні логарифми називаються також Неперовими на ім'я винахідника логарифмів, шотландського математика Непера(1550-1617 рр.), а десяткові логарифми - Бриггові на ім'я професора Брігга(Сучасника і друга Непера), вперше склав таблиці цих логарифмів.
278. Перетворення негативного логарифму на такий, у якого мантиса позитивна, і зворотне перетворення. Ми бачили, що логарифми чисел, менших за 1, негативні. Значить, вони складаються з негативної характеристики та негативної мантиси. Такі логарифми завжди можна перетворити так, що у них мантиса буде позитивною, а характеристика залишиться негативною. Для цього достатньо додати до мантиси позитивну одиницю, а до характеристики негативну (від чого, звичайно, величина логарифму не зміниться).
Якщо, наприклад, ми маємо логарифм - 2,0873 , То можна написати:
- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,
або скорочено:
Назад, будь-який логарифм з негативною характеристикою і позитивною мантисою можна перетворити на негативний. Для цього достатньо до позитивної мантиси прикласти негативну одиницю, а до негативної характеристики - позитивну: так, можна написати:

279. Опис чотиризначних таблиць.Для вирішення більшості практичних завданьцілком достатні чотиризначні таблиці, поводження з якими дуже просто. Таблиці ці (з написом на верху їх „логарифми”) поміщені наприкінці цієї книги, а невелика частина їх (для пояснення розташування) надрукована на цій сторінці, що містить мантиси.
Логарифми.

логарифмів всіх цілих чисел від 1 до 9999 включно, обчислені з чотирма десятковими знаками, причому останній із цих знаків збільшено на 1 у всіх тих випадках, коли 5-й десятковий знакмав би виявитися 5 або більше 5; отже, 4-значні таблиці дають наближені мантиси з точністю до 1 / 2 десятитисячної частки (з нестачею чи з надлишком).
Так як характеристику логарифму цілого числа або десяткового дробу ми можемо, на підставі властивостей десяткових логарифмів, проставити безпосередньо, то з таблиць повинні взяти тільки мантиси; при цьому треба згадати, що положення коми в десятковому числі, і навіть число нулів, що стоять наприкінці числа, немає впливу величину мантиси. Тому при знаходженні мантиси по даному числуми відкидаємо в тому числі кому, а також і нулі на кінці його, якщо такі є, і знаходимо мантису утвореного після цього цілого числа. При цьому можуть бути такі випадки.
1) Ціла кількість складається з 3-х цифр.Наприклад, нехай треба знайти мантису логарифму числа 536. Перші дві цифри цього числа, тобто 53, знаходимо в таблицях у першому зліва вертикальному стовпці (див. таблицю). Знайшовши число 53, просуваємось від нього по горизонтальному рядку вправо до перетину цього рядка з вертикальним стовпцем, що проходить через ту з цифр 0, 1, 2, 3,... 9, поставлених нагорі (і внизу) таблиці, яка є 3- ю цифру даного числа, т. е. у прикладі цифру 6. У перетині отримаємо мантису 7292 (т. е. 0,7292), що належить логарифму числа 536. Подібно до цього для числа 508 знайдемо мантису 0,7059, для числа 50 0,6990 тощо.
2) Ціле число складається з 2-х чи 1-ї цифри.Тоді подумки приписуємо до цього числу один або два нулі і знаходимо мантису для тризначного числа, що утворився таким чином. Напр., до 51 приписуємо один нуль, від чого отримуємо 510 і знаходимо мантису 7070; до числа 5 приписуємо 2 нуля і знаходимо мантису 6990 і т.д.
3) Ціла кількість виражається 4 цифрами.Напр., треба визначити мантису log 5436. Тоді спочатку знаходимо в таблицях, як було зазначено, мантису для числа, зображеного першими трьома цифрами цього числа, т. е. для 543 (ця мантиса буде 7348); потім просуваємося від знайденої мантиси горизонтальним рядком направо (у праву частинутаблиці, розташовану за жирною вертикальною рисою) до перетину з вертикальним стовпцем, що проходить через ту з цифр: 1, 2 3,... 9, що стоять на верху (і в низу) цієї частини таблиці, яка являє собою 4 цифру даного числа, тобто в нашому прикладі цифру 6. У перетині знаходимо поправку (число 5), яку треба додати в розумі до мантиси 7348, щоб отримати мантису числа 5436; ми отримаємо таким чином мантису 0,7353.
4) Ціле число виражається 5 чи більше цифрами.Тоді відкидаємо всі цифри, крім перших 4-х, і беремо наближене чотиризначне число, причому останню цифру збільшуємо на 1 в тому. у випадку, коли відкидається 5-а цифра числа є 5 або більше 5. Так, замість 57842 ми беремо 5784, замість 30257 беремо 3026, замість 583263 беремо 5833 тощо. Для цього округленого чотиризначного числа знаходимо мантису так, як було пояснено.
Керуючись цими вказівками, знайдемо для прикладу логарифми наступних чисел:
36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.
Насамперед, не звертаючись до таблиць, проставимо одні характеристики, залишаючи місце для мантис, які випишемо після:
log 36,5 = 1, .... log 0,00345 = 3, ....
log 804,7 = 2,.... log 7,2634 = 0,....
log 0,26 = 1,.... log 3456,86 = 3,....
log 36,5 = 1,5623; log 0,00345 = 3,5378;
log 804,7 = 2,9057; log 7,2634 = 0,8611;
log 0,26 = 1,4150; log 3456,86 = 3,5387.
280. Зауваження. У деяких чотиризначних таблицях (напр., у таблицях В. Лорченко та Н. Оглобліна, С. Глазенапа, Н. Каміньщикова) поправки на 4 цифру даного числа не вміщені. Маючи справу з такими таблицями, доводиться ці поправки знаходити за допомогою простого обчислення, Яке можна виконувати на підставі наступної істини: якщо числа перевищують 100, а різниці між ними менше 1, то без чутливої похибки можна прийняти, що різниці між логарифмами пропорційні різницям між відповідними числами . Нехай, напр., треба знайти мантису, що відповідає числу 5367. Мантісса ця, звичайно, та сама, що і для числа 536,7. Знаходимо в таблицях для числа 536 мантису 7292. Порівнюючи цю мантису з сусідньою вправо мантисою 7300, відповідної числа 537 ми помічаємо, що якщо число 536 збільшиться на 1, то мантиса його збільшиться на 8 десятитисячних (8 є так звана таблічна різницяміж двома сусідніми мантисами); якщо ж число 536 збільшиться на 0,7, то його мантиса збільшиться не на 8 десятитисячних, а на деяке менше х десятитисячне, яке, відповідно до допущеної пропорційності, має задовольняти пропорції:
х : 8 = 0,7: 1; звідки х = 8 07 = 5,6,
що за округленням становить 6 десятитисячних. Отже, мантиса для числа 536,7 (і отже, для числа 5367) буде: 7292 + 6 = 7298.
Зауважимо, що перебування за двома рядами числа проміжного числа, що стоять у таблицях, називається інтерполювання.Інтерполювання, описане тут, називається пропорційним, оскільки воно засноване на припущенні, що зміна логарифму пропорційна до зміни числа. Воно називається також лінійним, оскільки передбачає, що графічно зміна логарифмічної функції виражається прямою лінією.
281. Межа похибки наближеного логарифму.Якщо число, якого логарифм знаходиться, є число точне, то за межу похибки його логарифму, знайденого але 4-значним таблицям, можна прийняти, як ми говорили в , прийняти 1 / 2 десятитисячної частки. Якщо ж це число не точне, то до цієї межі похибки треба ще додати межу іншої похибки, що походить від неточності самого числа. Доведено (ми опускаємо цей доказ), що за таку межу можна прийняти твір
a(d +1) десятитисячних.,
в котрому а є межа похибки самого неточного числа у припущенні, що у його цілій частині взято 3 цифри, a d таблична різниця мантис, що відповідають двом послідовним тризначним числам, між якими полягає дане неточне число. Таким чином, межа остаточної похибки логарифму виразиться тоді формулою:
1 / 2 + a(d +1) десятитисячних
приклад. Знайти log π , приймаючи за π наближене число 3,14, точне до 1 / 2 сотий.
Перенісши в числі 3,14 кому після 3-ї цифри, рахуючи зліва, ми отримаємо тризначне число 314, точне до 1 / 2 одиниці; значить, межа похибки неточного числа, тобто те, що ми позначили буквою а , єгь 1 / 2 З таблиць знаходимо:
log 3,14 = 0,4969.
Таблична різниця d між мантисами чисел 314 і 315 дорівнює 14, тому похибка знайденого логарифму буде меншою
1 / 2 + 1 / 2 (14 +1) = 8 десятитисячних.
Так як про логарифм 0,4969 ми не знаємо, чи з недоліком він чи з надлишком, то можемо тільки ручатися, що точний логарифм π полягає між 0,4969 - 0,0008 та 0,4969 + 0,0008, тобто 0,4961< log π < 0,4977.
282. Знайти число за цим логарифмом. Для знаходження числа з цього логарифму можуть бути самі таблиці, якими перебувають мантиси даних чисел; але зручніше користуватися іншими таблицями, у яких вміщено звані антилогарифмы, т. е. числа, відповідні даним мантисам. Таблиці ці, позначені написом зверху „антилогарифми", поміщені наприкінці цієї книги слідом за таблицями логарифмів; невелика частина їх поміщена на цій сторінці (для пояснення).

Нехай дана 4-значна мантіса 2863 (на характеристику не звертаємо уваги) і потрібно знайти відповідне ціле число. Тоді, маючи таблиці антилогарифмів, треба користуватися ними так само, як було раніше пояснено для знаходження мантис за цим числом, а саме: перші 2 цифри мантиси ми знаходимо в першому зліва стовпці. Потім просуваємось від цих цифр по горизонтальному рядку вправо до перетину з вертикальним стовпцем, що йде від 3-ї цифри мантиси, яку треба шукати у верхньому рядку (або в нижньому). У перетині знаходимо чотиризначне число 1932, відповідне мантисі 286. Потім від цього числа просуваємось далі по горизонтальному рядку направо до перетину з вертикальним стовпцем, що йде від 4-ї цифри мантиси, яку треба знайти нагорі (або внизу) серед поставлених там цифр 1 , 3, ... 9. У перетині ми знаходимо поправку 1, яку треба докласти (в розумі) до знайденого раніше числа 1032, щоб отримати число, що відповідає мантисі 2863.
Таким чином, число це буде 1933 року. Після цього, звертаючи увагу на характеристику, треба в числі 1933 року поставити зайняту на належному місці. Наприклад:
якщо log x = 3,2863, то х = 1933,
„ log x = 1,2863, „ х = 19,33,
, log x = 0,2&63, „ х = 1,933,
„ log x = 2 ,2863, „ х = 0,01933
Ось ще приклади:
log x = 0,2287, х = 1,693,
log x = 1 ,7635, х = 0,5801,
log x = 3,5029, х = 3184,
log x = 2 ,0436, х = 0,01106.
Якщо в мантисі вказано 5 або більше цифр, то беремо лише перші 4 цифри, відкидаючи інші (і збільшуючи 4 цифру на 1, якщо 5 цифра є п'ять або більше). Напр., замість мантиси 35478 беремо 3548, замість 47562 беремо 4756.
283. Зауваження.Поправку на 4-ту та наступні цифримантиси можна шукати і за допомогою інтерполювання. Так, якщо мантиса буде 84357, то, знайшовши число 6966, відповідне мантисі 843 ми можемо міркувати далі так: якщо мантиса збільшується на 1 (тисячну), тобто зробить 844, то число, як видно з таблиць, збільшиться на 1 одиниць; якщо ж мантиса збільшиться не так на 1 (тисячну), але в 0,57 (тисячної), то число збільшиться на х одиниць, причому х має задовольняти пропорції:
х : 16 = 0,57: 1, звідки х = 16 0,57 = 9,12.
Отже, число, що шукається, буде 6966+ 9,12 = 6975,12 або (обмежуючись лише чотирма цифрами) 6975.
284. Межа похибки знайденого числа.Доведено, що в тому випадку, коли в знайденому числі кома стоїть після 3-ї цифри зліва, тобто коли характеристика логарифму є 2, за межу похибки можна прийняти суму
![]()
де а є межа похибки логарифму (виражений у десятитисячних частках), яким знаходилося число, і d - Різниця між мантисами двох тризначних послідовних чисел, між якими полягає знайдене число (з комою після 3-ї цифри зліва). Коли характеристика буде не 2, а якась інша, то в знайденому числі кому доведеться перенести вліво або вправо, тобто розділити або помножити число на деякий ступінь 10. При цьому похибка результату також розділиться або помножиться на той же ступінь 10.
Нехай, наприклад, ми шукаємо число за логарифмом 1,5950 , Про яке відомо, чого він точний до 3 десятитисячних; значить, тоді а = 3 . Число, що відповідає цьому логарифму, знайдене за таблицею антилогарифмів, є 39,36 . Перенісши кому після 3-ї цифри зліва, матимемо число 393,6 , що полягає між 393 і 394 . З таблиць логарифмів бачимо, що різниця між мантисами, що відповідають цим двом числам, становить 11 десятитисячних; значить d = 11 . Похибка числа 393,6 буде меншою

Отже, похибка числа 39,36 буде менше 0,05 .
285. Дії над логарифмами із негативними характеристиками.Додавання і віднімання логарифмів не становлять жодних труднощів, як це видно з наступних прикладів:

Не уявляє жодних труднощів також і множення логарифму на позитивне число, напр.:

В останньому прикладі окремо помножено позитивну мантису на 34, потім негативна характеристикана 34.
Якщо логарифм про негативну характеристику і позитивну мантису множиться на негативне число, то надходять двояко: або попередньо даний логарифм звертають в негативний, або множать окремо мантису і характеристику і результати з'єднують разом, наприклад:
3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;
3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.
При розподілі можуть бути два випадки: 1) негативна характеристика ділиться та 2) не поділяється на дільник. У першому випадку окремо ділять характеристику та мантису:
10 ,3784: 5 = 2 ,0757.
У другому випадку додають до характеристики стільки негативних одиниць, щоб число, що утворилося, ділилося на дільник; до мантиси додають стільки ж позитивних одиниць:
3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.
Це перетворення треба здійснювати в умі, так що дія розташовується так:
286. Заміна віднімаються логарифмів доданками.При обчисленні якогось складного виразудопомогою логарифмів доводиться деякі логарифми складати, інші віднімати; у разі, при звичайному методі здійснення дій, знаходять окремо суму доданків логарифмів, потім суму віднімаються і з першої суми віднімають другу. Напр., якщо маємо:
log х = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,
то звичайне виконання процесів розташується так:

Є однак можливість замінити віднімання додаванням. Так:

Тепер можна розмістити обчислення так:

287. Приклади обчислень.
Приклад 1. Обчислити вираз:

якщо А = 0,8216, = 0,04826, С = 0,005127і D = 7,246.
Логарифмуємо цей вираз:
log х= 1 / 3 log A + 4 log В - 3 log С - 1 / 3 log D
Тепер, щоб уникнути зайвої втрати часу і зменшення можливості помилок, передусім розташуємо всі обчислення, не виконуючи поки що їх і звертаючись, отже, до таблиць:

Після цього беремо таблиці та проставляємо логарифми на залишених вільних місцях:

Межа похибки.Спочатку знайдемо межу похибки числа x 1 = 194,5 , рівний:
![]()
Отже, перш за все треба знайти а т. е. межа похибки наближеного логарифму, виражений у десятитисячних частках. Припустимо, що дані числа А, В, Сі Dвсі точні. Тоді похибки в окремих логарифмах будуть такі (у десятитисячних частках):
в logА.......... 1 / 2
в 1/3 log A......... 1 / 6 + 1 / 2 = 2 / 3
( 1 / 2 додана тому, що при розподілі на 3 логарифми 1,9146 ми округлили приватне, відкинувши 5-у цифру його, і, отже, зробили ще помилку, меншу 1 / 2 десятитисячний).

Тепер знаходимо межу похибки логарифму:
а = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (Десятитисячних).
Визначимо далі d . Так як x 1 = 194,5 , то 2 цілих послідовних числа, між якими полягає x 1 будуть 194 і 195 . Таблична різниця d між мантисами, що відповідають цим числам, дорівнює 22 . Значить, межа похибки числа x 1 є:
Так як x = x 1 : 10, то межа похибки в числі x дорівнює 0,3:10 = 0,03 . Таким чином, знайдене нами число 19,45 відрізняється від точного числа менше, ніж на 0,03 . Так як ми не знаємо, з нестачею чи з надлишком знайдено наше наближення, то можемо лише ручатися, що
19,45 + 0,03 > х > 19,45 - 0,03 , тобто.
19,48 > х > 19,42 ,
і тому, якщо приймемо х =19,4 , То будемо мати наближення з недоліком з точністю до 0,1.
приклад 2.Обчислити:
х = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .
Оскільки негативні числа немає логарифмів, то попередньо знаходимо:
х" = (2,31) 3 5 √72
з розкладання:
log х"= 3 log 2,31 + 1/5 log72.
Після обчислення виявиться:
х" = 28,99 ;
отже,
x = - 28,99 .
Приклад 3. Обчислити:
![]()
Суцільного логарифмування тут застосувати не можна, так як під знаком кореня стоїть розуму. У таких випадках обчислюють формулу частинами.
Спочатку знаходимо N = 5 √8 , потім N 1 = 4 √3 ; далі простим додаванням визначаємо N+ N 1 , і, нарешті, обчислюємо 3 √N+ N 1 ; виявиться:
N = 1,514, N 1 = 1,316 ; N+ N 1 = 2,830 .
log x= log 3 √ 2,830 = 1 / 3 log 2,830 = 0,1506 ;
x = 1,415 .
Розділ четвертий.
Показові та логарифмічні рівняння.
288. Показовими рівняннями називаються такі, у яких невідоме входить до показника ступеня, а логарифмічними- такі, у яких невідоме входить під знаком log. Такі рівняння можуть бути дозволені тільки в окремих випадках, причому доводиться ґрунтуватися на властивостях логарифмів і на тому початку, що коли числа рівні, то рівні та їх логарифми, і, якщо логарифми рівні, то рівні і відповідні їм числа.
приклад 1.Вирішити рівняння: 2 x = 1024 .
Логарифмуємо обидві частини рівняння:
приклад 2.Вирішити рівняння: a 2x - a x = 1 . Поклавши a x = у , отримаємо квадратне рівняння:
y 2 - у - 1 = 0 ,

Так як 1-√5 < 0 , то останнє рівняння неможливе (функція a x завжди є число позитивне), а перше дає:
![]()
приклад 3.Вирішити рівняння:
log ( а + x) + log ( b + х) = log ( з + x) .
Рівняння можна написати так:
log [( а + x) (b + х)] = log ( з + x) .
З рівності логарифмів укладаємо про рівність чисел:
(а + x) (b + х) = з + x .
Це є квадратне рівняння, рішення якого не становить труднощів.
Розділ п'ятий.
Складні відсотки, термінові сплати та строкові внески.
289. Основне завдання складні відсотки.В яку суму звернеться капітал а рублів, відданий у зростання по р складних відсотків, по завершенню t років ( t - ціле число)?
Кажуть, що капітал віддано за складними відсотками, якщо беруться до уваги так звані „відсотки на відсотки”, тобто якщо належні на капітал відсоткові гроші приєднуються наприкінці кожного року до капіталу для нарощення їх відсотками у наступні роки.
Кожен рубль капіталу, відданого по р %, протягом одного року принесе прибутки p / 100 рубля, і, отже, кожен рубль капіталу через 1 рік звернеться до 1 + p / 100 рубля (напр., якщо капітал віддано по 5 % , то кожен карбованець його через рік звернеться в 1 + 5 / 100 , тобто в 1,05 рубля).
Позначивши для стислості дріб p / 100 однією буквою, напр, r , можемо сказати, що кожен рубль капіталу через рік звернеться в 1 + r рублів; отже, а рублів звернуться через 1 рік у а (1 + r ) руб. Ще через рік, тобто через 2 роки від початку зростання, кожен рубль з цих а (1 + r ) руб. звернеться знову в 1 + r руб.; значить, весь капітал звернеться до а (1 + r ) 2 руб. Так само знайдемо, що через три роки капітал буде а (1 + r ) 3 , через чотири роки буде а (1 + r ) 4 ,... взагалі через t років, якщо t є ціле число, він звернеться до а (1 + r ) tруб. Таким чином, позначивши через Аостаточний капітал, матимемо наступну формулу складних відсотків:
А = а (1 + r ) tде r = p / 100 .
приклад.Нехай a =2300 руб., p = 4, t=20 років; тоді формула дає:
r = 4 / 100 = 0,04 ; А = 2300 (1,04) 20 .
Щоб обчислити А, застосовуємо логарифми:
log a = log 2 300 + 20 log 1,04 = 3,3617 + 20 0,0170 = 3,3617 +0,3400 = 3,7017.
A = 5031карбованець.
Зауваження.У цьому прикладі нам довелося log 1,04помножити на 20 . Оскільки число 0,0170 є наближене значення log 1,04з точністю до 1 / 2 десятитисячної частки, то добуток цього числа на 20 буде точно тільки до 1 / 2 20, тобто до 10 десятитисячних = 1 тисячний. Тому в сумі 3,7017 ми можемо ручатися як за цифру десятитисячних, а й цифру тисячних. Щоб у подібних випадках можна було отримати більшу точність, краще для числа 1 + r брати логарифми не 4-значні, а з більшим числомнапр. 7-значні. Для цієї мети ми наводимо тут невелику табличку, в якій виписані 7-значні логарифми для найбільш уживаних значень р .

290. Основне завдання термінові сплати.Хтось зайняв а рублів за р % з умовою погасити борг, разом із належними нею відсотками, в t років, вносячи наприкінці кожного року ту саму суму. Якою має бути ця сума?
Сума x , що вноситься щорічно за таких умов, називається терміновою сплатою. Позначимо знову буквою r щорічні відсоткові гроші з 1 руб., Т. е. число p / 100 . Тоді до кінця першого року борг а зростає до а (1 + r ), а за сплатою х рублів він стане а (1 + r )-х .
До кінця другого року кожен рубль цієї суми знову звернеться до 1 + r рублів, і тому борг буде [ а (1 + r )-х ](1 + r ) = а (1 + r ) 2 - x (1 + r ), а за сплатою x рублів виявиться: а (1 + r ) 2 - x (1 + r ) - х . Так само переконаємося, що до кінця 3-го року борг буде
а (1 + r ) 3 - x (1 + r ) 2 - x (1 + r ) - x ,
і взагалі і кінцю t -го року він виявиться:
а (1 + r ) t - x (1 + r ) t -1 - x (1 + r ) t -2 ... - x (1 + r ) - x , або
а (1 + r ) t - x [ 1 + (1 + r ) + (1 + r ) 2 + ...+ (1 + r ) t -2 + (1 + r ) t -1 ]
Багаточлен, що стоїть усередині дужок, становить суму членів геометричній прогресії; у якої перший член є 1 , останній ( 1 + r ) t -1, а знаменник ( 1 + r ). За формулою для суми членів геометричної прогресії (відділ 10 розділ 3 § 249) знаходимо:
і величина боргу після t -ої сплати буде:
![]()
За умовою завдання, борг наприкінці t -го року повинен дорівнювати 0 ; тому:
![]() звідки
звідки
![]()
При обчисленні цієї формули термінових сплатза допомогою логарифмів ми повинні спочатку знайти допоміжне число N = (1 + r ) tз логарифму: log N= t log (1 + r) ; знайшовши N, віднімемо з нього 1, тоді отримаємо знаменник формули для х, після чого вторинним логарифмуванням знайдемо:
log х= log a+ log N + log r - log (N - 1).
291. Основне завдання на строкові внески.Хтось вносить до банку на початку кожного року ту саму суму а руб. Визначити, який капітал утворюється з цих внесків після закінчення t років, якщо банк платить за р складних процентів.
Позначивши через r щорічні відсоткові гроші з 1 карбованця, тобто. p / 100 , розмірковуємо так: до кінця першого року капітал буде а (1 + r );
на початку 2-го року до цієї суми додасться а рублів; значить, у цей час капітал виявиться а (1 + r ) + a . До кінця 2-го року він буде а (1 + r ) 2 + а (1 + r );
на початку 3-го року знову вноситься а рублів; значить, у цей час капітал буде а (1 + r ) 2 + а (1 + r ) + а ; до кінця 3-го він виявиться а (1 + r ) 3 + а (1 + r ) 2 + а (1 + r ) Продовжуючи ці міркування далі, знайдемо, що до кінця t -го року шуканий капітал Aбуде:

Такою є формула термінових внесків, що робляться на початку кожного року.
Ту ж формулу можна отримати і таким міркуванням. перший внесок у а рублів, перебуваючи у банку t років, звернеться, згідно з формулою складних відсотків, а (1 + r ) tруб. Другий внесок, перебуваючи у банку на один рік менше, тобто. t - 1 років, звернеться в а (1 + r ) t-1руб. Подібно до цього третій внесок дасть а (1 + r ) t-2і т. д., і, нарешті, останній внесок, перебуваючи в банку лише 1 рік, звернеться до а (1 + r ) руб. Отже, остаточний капітал Aруб. буде:
A= а (1 + r ) t + а (1 + r ) t-1 + а (1 + r ) t-2 + . . . + а (1 + r ),
що після спрощення дає знайдену вище формулу.
При обчисленні допомогою логарифмів цієї формули треба зробити так само, як і при обчисленні формули термінових сплат, тобто спочатку знайти число N = ( 1 + r ) tза його логарифмом: log N= t log(1 + r ), потім число N-1і вже тоді логарифмувати формулу:
log A = log a+ log (1 + r) + log (N - 1) - 1оgr
Зауваження.Якби терміновий внесок у а руб. провадився не на початку, а наприкінці кожного року (як, напр., вноситься термінова сплата х для погашення боргу), то, розмірковуючи подібно до попереднього, знайдемо, що до кінця t -го року шуканий капітал А"руб. буде (вважаючи у тому числі й останній внесок а руб., що не приносить відсотків):
A"= а (1 + r ) t-1 + а (1 + r ) t-2 + . . . + а (1 + r ) + а
що одно:
![]()
тобто. А"виявляється в ( 1 + r ) раз менше А, Що й треба було очікувати, тому що кожен рубль капіталу А"лежить у банку роком менше, ніж відповідний карбованець капіталу А.
Визначення логарифму
Логарифмом числа b на підставі а називається показник ступеня, в який потрібно звести а щоб отримати b .
Числом ев математиці прийнято позначати межу, якої прагнути вираз
Число еє ірраціональним числом - Числом, несумірним з одиницею, воно не може бути точно вираженим ні цілим ні дробовим раціональнимчислом.
Літера е- перша буква латинського слова exponere- виставляти напоказ, звідси в математиці назва експоненційна- Показова функція.
Число ешироко застосовується в математиці, і в усіх науках, які так чи інакше застосовують для своїх потреб математичні розрахунки.
Логарифми. Властивості логарифмів
Визначення: Логарифмом позитивного числа b на підставі називається показник ступеня с, в який треба звести число а щоб отримати число b.

Основна логарифмічна тотожність:


7) Формула переходу до нової основи:
lna = log e a, e ≈ 2,718…
Завдання та тести на тему «Логорифми. Властивості логарифмів»
- Логарифми Важливі темидля повторення ЄДІ з математики
Для успішного виконання завдань на цю тему Ви повинні знати визначення логарифму, властивості логарифмів, основну логарифмічну тотожність, визначення десяткового та натурального логарифмів. Основні типи завдань з цієї теми — це завдання на обчислення та перетворення логарифмічних виразів. Розглянемо їхнє рішення на наступних прикладах.
Рішення:Використовуючи властивості логарифмів, отримаємо
Рішення:використовуючи властивості ступеня, отримаємо
1) (2 2) log 2 5 = (2 log 2 5) 2 = 5 2 = 25
Властивості логарифмів, формулювання та докази.
Логарифми мають поруч характерних властивостей. У цій статті ми розберемо основні властивості логарифмів. Тут ми дамо їх формулювання, запишемо властивості логарифмів як формул, покажемо приклади їх застосування, і навіть наведемо докази властивостей логарифмів.
Навігація на сторінці.
Основні властивості логарифмів, формули
Для зручності запам'ятовування та використання уявимо основні властивості логарифмівяк списку формул. У наступному пунктідамо їх формулювання, докази, приклади використання та необхідні пояснення.
і властивість логарифму добутку n позитивних чисел: log a (x 1 · x 2 · ... · x n) = log a x 1 +log a x 2 + ... >0, …, x n >0 .
 , де a>0, a≠1, x>0, y>0.
, де a>0, a≠1, x>0, y>0. , a>0, a≠1, b>0, b≠1.
, a>0, a≠1, b>0, b≠1. , a>0 , a≠1 , b>0 , p і q – дійсні числа, q≠0 , зокрема при b=a маємо
, a>0 , a≠1 , b>0 , p і q – дійсні числа, q≠0 , зокрема при b=a маємо  .
.Формулювання та докази властивостей
Переходимо до формулювання та доказу записаних властивостей логарифмів. Всі властивості логарифмів доводяться на основі визначення логарифму і основного логарифмічного тотожності, що випливає з нього, а також властивостей ступеня.
Почнемо зі властивості логарифму одиниці. Його формулювання таке: логарифм одиниці дорівнює нулю, тобто, log a 1=0для будь-якого a>0, a≠1. Доказ не викликає складнощів: оскільки a 0 =1 для будь-якого a , що задовольняє зазначеним вище умовам a>0 і a≠1 , то рівність log a 1=0 відразу випливає з визначення логарифму.
Наведемо приклади застосування розглянутої якості: log 3 1=0 , lg1=0 і .
Переходимо до наступної властивості: логарифм числа, рівного підставі, дорівнює одиниці , тобто, log a a=1при a>0, a≠1. Справді, оскільки a 1 =a для будь-якого a , то визначення логарифму log a a=1 .
Прикладами використання цієї властивості логарифмів є рівності log 5 5 = 1, log 5,6 5,6 і lne = 1 .
Логарифм ступеня числа, що дорівнює підставі логарифму, дорівнює показникуступеня. Цій властивості логарифму відповідає формула виду log a a p = p, де a>0, a≠1 і p – будь-яке дійсне число. Ця властивість безпосередньо випливає з визначення логарифму. Зауважимо, що воно дозволяє відразу вказати значення логарифму, якщо є можливість уявити число під знаком логарифму у вигляді ступеня основи, детальніше про це ми поговоримо у статті обчислення логарифмів.
Наприклад, log 2 2 7 =7 , lg10 -4 =-4 і ![]() .
.
Логарифм твору двох позитивних чисел x та y дорівнює творулогарифмів цих чисел: log a (x · y) = log a x + log a y, a>0, a≠1. Доведемо властивість логарифму твору. У силу властивостей ступеня a log a x + log a y = a log a x a log a y , а так як по основному логарифмічної тотожності a log a x = x і a log a y = y , то a log a x log a y = x y. Таким чином, a log a x + log a y = x · y, звідки за визначенням логарифму випливає рівність, що доводиться.
Покажемо приклади використання властивості логарифму добутку: log 5 (2·3)=log 5 2+log 5 3 ![]() .
.
Властивість логарифму твору можна узагальнити на твір кінцевого числа n позитивних чисел x 1 , x 2 , …, x n як log a (x 1 · x 2 · ... · x n) = log a x 1 + log a x 2 + ... + log a x n. Ця рівність без проблем доводиться методом математичної індукції.
Наприклад, натуральний логарифм твору можна замінити сумою трьох натуральних логарифмів чисел 4 , e , і .
Логарифм приватного двох позитивних чисел x та y дорівнює різницілогарифмів цих чисел. Властивості приватного логарифму відповідає формула виду  , де a>0, a≠1, x та y – деякі позитивні числа. Справедливість цієї формули доводиться як і формула логарифму твору: оскільки
, де a>0, a≠1, x та y – деякі позитивні числа. Справедливість цієї формули доводиться як і формула логарифму твору: оскільки  , то за визначенням логарифму
, то за визначенням логарифму  .
.
Наведемо приклад використання цієї властивості логарифму: ![]() .
.
Переходимо до властивості логарифму ступеня. Логарифм ступеня дорівнює добутку показника ступеня на логарифм модуля основи цього ступеня. Запишемо цю властивість логарифму ступеня у вигляді формули: log a b p = log a | b |, де a>0 , a≠1 , b та p такі числа, що ступінь b p має сенс і b p >0 .
Спочатку доведемо цю властивість для позитивних b. Основне логарифмічне тотожність дозволяє нам уявити число b як a log a b тоді b p = (a log a b) p , а отримане вираз в силу властивість ступеня дорівнює a p · log a b . Так ми приходимо до рівності b p = a p · log a b , з якого за визначенням логарифму укладаємо, що log a b p = p · log a b .
Залишилося довести цю властивість для негативних b. Тут зауважуємо, що вираз log a b p при негативних b має сенс лише при парних показниках ступеня p (оскільки значення ступеня b p має бути більшим за нуль, в іншому випадку логарифм не матиме сенсу), а в цьому випадку b p =|b| p. Тоді b p = | b | p = (a log a | b |) p = a p · log a | b | , Звідки log a b p = p log a | b | .
Наприклад,  і ln(-3) 4 =4·ln|-3|=4·ln3 .
і ln(-3) 4 =4·ln|-3|=4·ln3 .
Із попередньої властивості випливає властивість логарифму з кореня: логарифм кореня n -ого ступеня дорівнює добутку дробу 1/n на логарифм підкореного виразу, Тобто, , де a>0, a≠1,n - натуральне число, більше одиниці, b>0.
Доказ базується на рівності (дивіться визначення ступеня з дробовим показником), яке справедливе для будь-яких позитивних b і властивості логарифму ступеня:  .
.
Ось приклад використання цієї властивості: ![]() .
.
Тепер доведемо формулу переходу до нової основи логарифмувиду  . Для цього достатньо довести справедливість рівності log c b = log a b log c a . Основне логарифмічне тотожність дозволяє нам число b уявити як a log a b тоді log c b = log c a log a b . Залишилося скористатися властивістю логарифму ступеня: log ca log ab = log ab log ca . Так доведено рівність log c b = log a b log c a , а значить, доведено і формулу переходу до нової основи логарифму
. Для цього достатньо довести справедливість рівності log c b = log a b log c a . Основне логарифмічне тотожність дозволяє нам число b уявити як a log a b тоді log c b = log c a log a b . Залишилося скористатися властивістю логарифму ступеня: log ca log ab = log ab log ca . Так доведено рівність log c b = log a b log c a , а значить, доведено і формулу переходу до нової основи логарифму  .
.
Покажемо кілька прикладів застосування цієї властивості логарифмів: і  .
.
Формула переходу до нової основи дозволяє переходити до роботи з логарифмами, що мають «зручну» основу. Наприклад, з її допомогою можна перейти до натуральних або десяткових логарифмів, щоб можна було обчислити значення логарифму таблиці логарифмів. Формула переходу до нової основи логарифму також дозволяє в деяких випадках знаходити значення логарифму, коли відомі значення деяких логарифмів з іншими основами.
Часто використовується окремий випадок формули переходу до нової основи логарифму при c = b виду. Звідси видно, що log ab і log ba – взаємно зворотні числа. Наприклад,  .
.
Також часто використовується формула, яка зручна при знаходженні значень логарифмів. Для підтвердження своїх слів покажемо, як з її допомогою обчислюється значення логарифму . Маємо  . Для доказу формули достатньо скористатися формулою переходу до нової основи логарифму:
. Для доказу формули достатньо скористатися формулою переходу до нової основи логарифму:  .
.
Залишилося довести властивості порівняння логарифмів.
Скористаємося методом від неприємного. Припустимо, що за a 1 >1 , a 2 >1 і a 1 2 і за 0 1 справедливо log a 1 b≤log a 2 b . За властивостями логарифмів ці нерівності можна переписати як  і
і  відповідно, а з них випливає, що log b a 1 ≤ log b a 2 і log b a 1 ≥ log b a 2 відповідно. Тоді за властивостями ступенів з однаковими основами повинні виконуватися рівності b log b a 1 b log b a 2 і b log b a 1 b log b a 2 , тобто, a 1 a 2 . Так ми дійшли суперечності умові a 1 2 . На цьому доказ завершено.
відповідно, а з них випливає, що log b a 1 ≤ log b a 2 і log b a 1 ≥ log b a 2 відповідно. Тоді за властивостями ступенів з однаковими основами повинні виконуватися рівності b log b a 1 b log b a 2 і b log b a 1 b log b a 2 , тобто, a 1 a 2 . Так ми дійшли суперечності умові a 1 2 . На цьому доказ завершено.
Основні властивості логарифмів
- Матеріали до уроку
- Завантажити всі формули
- log a x n = n · log a x;
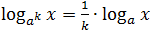

Логарифми, як і будь-які числа, можна складати, віднімати та всіляко перетворювати. Але оскільки логарифми – це не зовсім звичайні числа, тут є свої правила, які називаються основними властивостями.
Ці правила обов'язково треба знати – без них не вирішується жодне серйозне логарифмічне завдання. До того ж їх зовсім небагато - все можна вивчити за один день. Отже, почнемо.
Додавання та віднімання логарифмів
Розглянемо два логарифми з однаковими основами: log a x та log a y . Тоді їх можна складати і віднімати, причому:
Отже, сума логарифмів дорівнює логарифму добутку, а різниця - приватного логарифму. Зверніть увагу: ключовий моменттут - однакові підстави. Якщо підстави різні, ці правила не працюють!
Ці формули допоможуть обчислити логарифмічний виразнавіть тоді, коли окремі його частини не рахуються (див. урок «Що таке логарифм»). Погляньте на приклади – і переконайтесь:
Завдання. Знайдіть значення виразу: log 6 4 + log 6 9.
Оскільки підстави у логарифмів однакові, використовуємо формулу суми:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.
Завдання. Знайдіть значення виразу: log 2 48 − log 2 3.
Підстави однакові, використовуємо формулу різниці:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Завдання. Знайдіть значення виразу: log 3 135 − log 3 5.
Знову підстави однакові, тому маємо:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Як бачите, вихідні вирази складені з поганих логарифмів, які окремо не вважаються. Але після перетворень виходять цілком нормальні числа. На цьому факті побудовано багато контрольні роботи. Та що контрольні - подібні висловлюванняна повному серйозі (іноді - практично без змін) пропонуються на ЄДІ.
Винесення показника ступеня з логарифму
Тепер трохи ускладнимо завдання. Що, якщо у підставі чи аргументі логарифма стоїть ступінь? Тоді показник цього ступеня можна винести за знак логарифму за такими правилами:
Неважко помітити, що останнє правилослід їх перших двох. Але краще його все ж таки пам'ятати - в деяких випадках це значно скоротить обсяг обчислень.
Зрозуміло, всі ці правила мають сенс при дотриманні ОДЗлогарифма: a > 0, a ≠ 1, x > 0. І ще: вчіться застосовувати всі формули як зліва направо, а й навпаки, тобто. можна вносити числа, що стоять перед знаком логарифму, до самого логарифму. Саме це найчастіше й потрібне.
Завдання. Знайдіть значення виразу: log 7 49 6 .
Позбавимося ступеня в аргументі за першою формулою:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12
Завдання. Знайдіть значення виразу:
[Підпис до малюнка]
Зауважимо, що у знаменнику стоїть логарифм, основа та аргумент якого є точними ступенями: 16 = 2 4 ; 49 = 7 2 . Маємо:
 [Підпис до малюнка]
[Підпис до малюнка]
Думаю, до останньому прикладупотрібні пояснення. Куди зникли логарифми? До останнього моменту ми працюємо лише зі знаменником. Представили підставу і аргумент логарифму, що там стоїть, у вигляді ступенів і винесли показники - отримали «триповерховий» дріб.
Тепер подивимося на основний дріб. У чисельнику і знаменнику стоїть те саме число: log 2 7. Оскільки log 2 7 ≠ 0, можемо скоротити дріб - у знаменнику залишиться 2/4. За правилами арифметики, четвірку можна перенести в чисельник, що було зроблено. В результаті вийшла відповідь: 2.
Перехід до нової основи
Говорячи про правила складання та віднімання логарифмів, я спеціально підкреслював, що вони працюють лише за однакових підстав. А що, коли підстави різні? Що, якщо вони не є точними ступенями того самого числа?
На допомогу приходять формули переходу до нової основи. Сформулюємо їх як теореми:
Нехай даний логарифм log a x. Тоді для будь-якого числа c такого, що c > 0 і c ≠ 1, правильна рівність:
![]() [Підпис до малюнка]
[Підпис до малюнка]
Зокрема, якщо покласти c = x, отримаємо:
![]() [Підпис до малюнка]
[Підпис до малюнка]
З другої формули випливає, що можна міняти місцями основу та аргумент логарифму, але при цьому весь вислів «перевертається», тобто. логарифм опиняється у знаменнику.
Ці формули рідко зустрічаються у звичайних числових виразів. Оцінити, наскільки вони зручні, можна лише при розв'язанні логарифмічних рівнянь та нерівностей.
Втім, існують завдання, які взагалі не вирішуються інакше як переходом до нової основи. Розглянемо пару таких:
Завдання. Знайдіть значення виразу: log 5 16 · log 2 25.
Зауважимо, що в аргументах обох логарифмів стоять точні ступені. Винесемо показники: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
А тепер «перевернемо» другий логарифм:
[Підпис до малюнка]
Оскільки від перестановки множників твір не змінюється, ми спокійно перемножили четвірку та двійку, а потім розібралися з логарифмами.
Завдання. Знайдіть значення виразу: log 9 100 · lg 3.
Підстава та аргумент першого логарифму – точні ступені. Запишемо це і позбудемося показників:
[Підпис до малюнка]
Тепер позбудемося десяткового логарифму, перейшовши до нової основи:
[Підпис до малюнка]
Основне логарифмічне тотожність
Часто в процесі рішення потрібно представити число як логарифм на задану основу. У цьому випадку нам допоможуть формули:
- n = log a a n
-
У першому випадку число n стає показником ступеня, що стоїть у аргументі. Число n може бути абсолютно будь-яким, адже це просто значення логарифму.
Друга формула – це фактично перефразоване визначення. Вона так і називається: основна логарифмічна тотожність.
Справді, що буде, якщо число b звести на такий ступінь, що число b у цій мірі дає число a ? Правильно: вийде це число a . Уважно прочитайте цей абзац ще раз – багато хто на ньому «зависає».
Подібно до формул переходу до нової основи, основна логарифмічна тотожність іноді буває єдино можливим рішенням.
[Підпис до малюнка]
Зауважимо, що log 25 64 = log 5 8 - просто винесли квадрат із підстави та аргументу логарифму. Враховуючи правила множення ступенів з однаковою основою, отримуємо:
[Підпис до малюнка]
Якщо хтось не в курсі, це було справжнє завдання з ЄДІ 🙂
Логарифмічна одиниця та логарифмічний нуль
Насамкінець наведу дві тотожності, які складно назвати властивостями - швидше, це наслідки з визначення логарифму. Вони постійно зустрічаються у завданнях і, що дивно, створюють проблеми навіть для «просунутих» учнів.
- log a a = 1 – це логарифмічна одиниця. Запам'ятайте раз і назавжди: логарифм з будь-якої основи a від самої цієї основи дорівнює одиниці.
- log a 1 = 0 – це логарифмічний нуль. Підстава a може бути будь-яким, але якщо в аргументі стоїть одиниця - логарифм дорівнює нулю! Тому що a 0 = 1 – це прямий слідствоіз визначення.
Ось і всі властивості. Обов'язково потренуйтеся застосовувати їх на практиці! Завантажте шпаргалку на початку уроку, роздрукуйте її – і вирішуйте завдання.
Логарифм. Властивості логарифму (складання та віднімання).
Властивості логарифмувипливають із його визначення. І так логарифм числа bна підставі авизначається як показник ступеня, в який треба звести число a, щоб отримати число b(Логарифм існує тільки у позитивних чисел).
З цього формулювання випливає, що обчислення x=log a b, рівнозначне рішенню рівняння a x = b.Наприклад, log 2 8 = 3тому що 8 = 2 3 . Формулювання логарифму дає можливість довести, що якщо b=a з, то логарифм числа bна підставі aдорівнює з. Також ясно, що тема логарифмування тісно пов'язана з темою ступеня числа.
З логарифмами, як і з будь-якими числами, можна виконувати операції складання, відніманняі всіляко трансформувати. Але через те, що логарифми — це не зовсім ординарні числа, тут застосовні свої особливі правила, які називаються основними властивостями.
Складання та віднімання логарифмів.
Візьмемо два логарифми з однаковими підставами: log a xі log a y. Тоді зними можна виконувати операції складання та віднімання:
Як бачимо, сума логарифмівдорівнює логарифму твору, а різниця логарифмів- Логарифму приватного. Причому це правильно якщо числа ахі упозитивні та а ≠ 1.
Важливо звертати увагу, що основним аспектом даних формулах виступають одні й самі підстави. Якщо підстави відрізняються одна від одної, ці правила не застосовуються!
Правила складання та віднімання логарифмів з однаковими підставами читаються не тільки зліва на право, а й на оборот. В результаті ми маємо теореми логарифму твору та логарифму приватного.
Логарифм творудвох позитивних чисел дорівнює сумі їх логарифмів ; перефразовуючи цю теоремуотримаємо наступне, якщо числа а, xі упозитивні та а ≠ 1, то:
Логарифм приватногодвох позитивних чисел дорівнює різниці логарифмів ділимого та дільника. Говорячи інакше, якщо числа а, хі упозитивні та а ≠ 1, то:
Застосуємо вищевикладені теореми на вирішення прикладів:
Якщо числа xі унегативні, то формула логарифму творустає безглуздою. Так, заборонено писати:
оскільки вирази log 2 (-8) і log 2 (-4) взагалі не визначені ( логарифмічна функція у= log 2 хвизначено лише для позитивних значеньаргументу х).
Теорема творузастосовна не тільки для двох, а й для необмеженого числаспівмножників. Це означає, що для будь-якого натурального kта будь-яких позитивних чисел x 1 , x 2 , . . . ,x nіснує тотожність:
З теореми логарифму приватногоможна отримати ще одну властивість логарифму. Загальновідомо, що log a 1= 0, отже,
А значить має місце рівність:
Логарифми двох взаємно зворотних чисел по одному й тому підставі будуть різні друг від друга виключно знаком. Так:
Логарифм. Властивості логарифмів
Логарифм. Властивості логарифмів
Розглянемо рівність. Нехай нам відомі значення і ми хочемо знайти значення.
Тобто ми шукаємо показник ступеня, в який потрібно звести, щоб отримати .
Нехай
 змінна може приймати будь-яке дійсне значення, Тоді на змінні та накладаються такі обмеження: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>
змінна може приймати будь-яке дійсне значення, Тоді на змінні та накладаються такі обмеження: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>Якщо нам відомі значення і , і перед нами стоїть завдання знайти невідоме , то для цього вводиться математична дія, Яке називається логарифмування.
Щоб знайти значення, ми беремо логарифм числапо підставі :
Логарифмом числа на підставі називається показник ступеня, в який треба звести, щоб отримати .
Тобто основне логарифмічне тотожність:
o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>
є по суті математичним записом визначення логарифму.
Математична операція логарифмування є зворотною по відношенню до операції зведення в ступінь, тому властивості логарифмівтісно пов'язані з властивостями ступеня.
Перерахуємо основні властивості логарифмів:
(o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,
d>0″/>, 1″ title=”d1″/>
4.

5.

Наступна група властивостей дозволяє представити показник ступеня виразу, що стоїть під знаком логарифму, або стоїть на підставі логарифму як коефіцієнт перед знаком логарифму:
6.

7.

8.

9.

Наступна група формул дозволяє перейти від логарифму з цією основою до логарифму з довільною основою, і називається формулами переходу до нової основи:
10.

12. (наслідок з якості 11)

Наступні три властивості не дуже відомі, однак вони часто використовуються при вирішенні логарифмічних рівнянь або при спрощенні виразів, що містять логарифми:
13.

14.

15.

Приватні випадки:
 — десятковий логарифм
— десятковий логарифм — натуральний логарифм
— натуральний логарифмПри спрощенні виразів, що містять логарифми, застосовується загальний підхід:
1. Представляємо десяткові дробияк звичайних.
2. Змішані числаподаємо у вигляді неправильних дробів.
3. Числа, що стоять на підставі логарифму та під знаком логарифму розкладаємо на прості множники.
4. Намагаємось привести всі логарифми до однієї основи.
5. Застосовуємо властивості логарифмів.
Давайте розглянемо приклади спрощення виразів, що містять логарифми.
приклад 1.
Обчислити:
Спростимо всі показники ступенів: наше завдання привести їх до логарифмів, в основі яких стоїть те ж число, що й у підставі ступеня.
==(за якістю 7)=(за якістю 6) =
Підставимо показники, які у нас вийшли у вихідний вираз. Отримаємо:
Відповідь: 5,25
Приклад 2. Обчислити:

Приведемо всі логарифми до основи 6 (при цьому логарифми зі знаменника дробу «перекочують» до чисельника):
Розкладемо числа, що стоять під знаком логарифму на прості множники:
Застосуємо властивості 4 та 6:
Введемо заміну
Отримаємо:

Відповідь: 1
Логарифм . Основна логарифмічна тотожність.
Властивості логарифмів. Десятковий логарифм. Натуральний логарифм.
Логарифмом позитивного числа N на підставі (b > 0, b 1) називається показник ступеня x , в яку потрібно звести b щоб отримати N .
Цей запис рівнозначний наступному: b x = N .
Приміри: log 3 81 = 4 , так як 3 4 = 81 ;
log 1/3 27 = – 3, оскільки (1/3) - 3 = 3 3 = 27.
Наведене вище визначення логарифму можна записати у вигляді тотожності:

Основні властивостілогарифмів.
2) log 1 = 0, так як b 0 = 1 .
3) Логарифм твору дорівнює сумі логарифмів співмножників:
4) Логарифм приватного дорівнює різниці логарифмів діленого та дільника:
5) Логарифм ступеня дорівнює добутку показника ступеня на логарифм її основи:
Наслідком цієї властивості є таке: логарифм кореня дорівнює логарифму підкореного числа, поділеному на ступінь кореня:

6) Якщо на підставі логарифму знаходиться ступінь, то величину, зворотний показник ступеня, можна винести за знак лога риму:

Два останніх властивостіможна об'єднати в одне:

7) Формула модуля переходу (т. e. переходу від однієї основи логарифму до іншої основи):

В окремому випадку при N = aмаємо:

Десятичним логарифмом називається логарифм з основи 10. Він позначається lg, тобто. log 10 N= lg N. Логарифми чисел 10, 100, 1000, . p авни відповідно 1, 2, 3, …, тобто. мають стільки позитивних
одиниць, скільки нулів стоїть у логарифмованій кількості після одиниці. Логарифми чисел 0.1, 0.01, 0.001, . p авни відповідно –1, –2, –3, …, тобто. мають стільки негативних одиниць, скільки нулів стоїть в логарифмується перед одиницею (вважаючи і нуль цілих). Логарифми інших чисел мають дробову частинузвану мантисою. Ціла частиналогарифма називається характеристикою. Для практичного застосування десяткові логарифми найбільш зручні.
Натуральним логарифмом називається логарифм з основи е. Він позначається ln, тобто. log e N= ln N. Число еє ірраціональним, його наближене значення 2.718281828. Воно є межею, якої прагне число (1 + 1 / n) nпри необмеженому зростанні n(Див. перший чудова межа на сторінці "Межі числових послідовностей").
Як це не здасться дивним, натуральні логарифмивиявилися дуже зручними під час проведення різного родуоперацій, пов'язаних із аналізом функцій. Обчислення логарифмів на підставі ездійснюється набагато швидше, ніж з будь-якої іншої основи.
- Що потрібно сьогодні для усиновлення дитини у Росії? Усиновлення у Росії, крім відповідального особистого рішення, передбачає низку процедур державної перевірки кандидатів. Жорсткий відбір на підготовчому етапісприяє більше […]
- Відомості безкоштовно по ІПН або ОГРН з реєстру податкової по всій Росії - онлайн На Єдиному порталіПодаткові послуги можуть бути отримані відомостями про державної реєстрації юридичних осіб, індивідуальних підприємців, […]
- Покарання за їзду без документів ( водійські права, страховка, СТС) Іноді за забудькуватістю водії сідають за кермо без ВУ та отримують штраф за їзду без документів. Нагадаємо, що автоаматор за кермом при собі в обов'язковому порядку […]
- Квіти чоловіків. Які квіти можна подарувати чоловікові? Які квіти можна подарувати чоловікові? "Чоловічих" квітів не так багато, але є такі, які дарують чоловікам. Маленький список квітів перед вами: Хризантеми. Троянди. Гвоздики. […]
- Службова записка– це спеціальна формадокумента, що використовується в внутрішньому середовищіпідприємства та служить для швидкого вирішенняпоточні виробничі проблеми. Зазвичай цей документ складається з метою внесення будь-якого […]
- Коли і як отримати накопичувальну частину пенсії в Ощадбанку? Ощадбанк є банк-партнер державного пенсійного фонду. На підставі цього громадяни, які оформили накопичувальну пенсію, могли переводити до нього накопичувальну частину […]
- Дитячі посібники в Ульяновську та Ульянівській областіу 2018 році Крім того, у всіх суб'єктах працюють програми, затверджені федеральним законодавством. Розберемо, хто та на які пільги може розраховувати. Як регіональна влада […]
- Детальний посібник, як скласти довіреність на представлення інтересів фізичної особиу суді У цивільному чи арбітражному позові, в адміністративній чи кримінальній справі інтереси і позивача, і відповідача можуть представлятися повіреним: […]



